最小生成树 Minimum Spanning Tree

0.构建最小生成树

• 两种解法的思路

• 1584-连接所有点的最小费用

给你一个points 数组，表示 2D 平面上的一些点，其中 points[i] = [xi, yi] 。

连接点 [xi, yi] 和点 [xj, yj] 的费用为它们之间的 曼哈顿距离 ：|xi - xj| + |yi - yj| ，其中 |val| 表示 val 的绝对值。

请你返回将所有点连接的最小总费用。只有任意两点之间 有且仅有 一条简单路径时，才认为所有点都已连接。
1
2
3
4
5

示例 1：

输入：points = [[0,0],[2,2],[3,10],[5,2],[7,0]]
输出：20
1
2

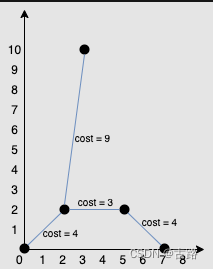
解释：
我们可以按照上图所示连接所有点得到最小总费用，总费用为 20 。
注意到任意两个点之间只有唯一一条路径互相到达。
1
2
3
4

示例 2：
输入：points = [[3,12],[-2,5],[-4,1]]
输出：18

示例 3：
输入：points = [[0,0],[1,1],[1,0],[-1,1]]
输出：4

示例 4：
输入：points = [[-1000000,-1000000],[1000000,1000000]]
输出：4000000

示例 5：
输入：points = [[0,0]]
输出：0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

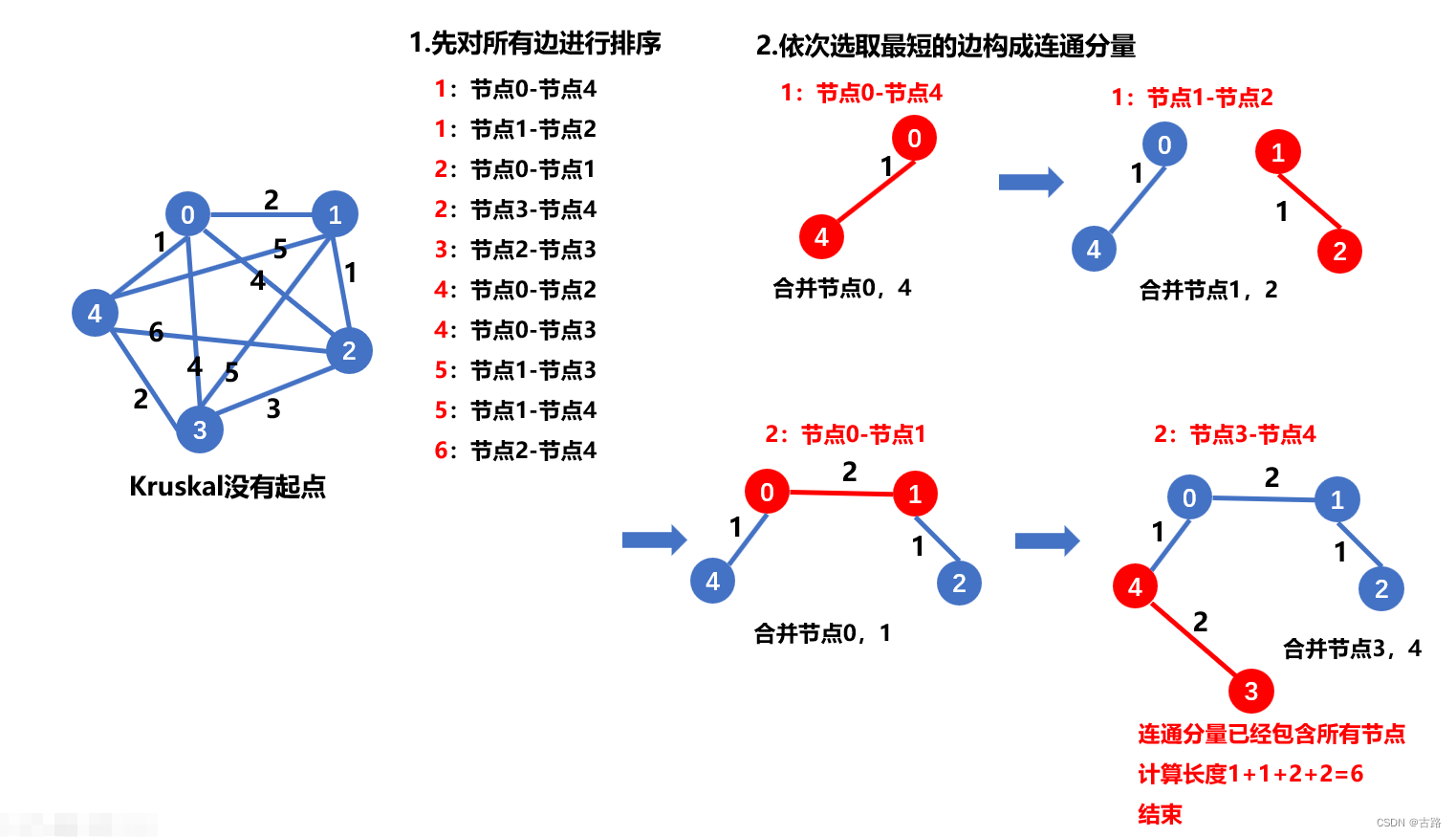
1.Kruskal算法

• 并查集的路径压缩：

Kruskal算法思路：

• 将每个边按权重从小到大的排序
• 依次添加边
• 利用并查集判断新添加的边是否回环

/*
 * @Date: 2022-06-30
 * @Author: bFeng
 */
/*
 * @lc app=leetcode.cn id=1584 lang=cpp
 *
 * [1584] 连接所有点的最小费用
 */

// @lc code=start
class UnionFind {
 public:
  UnionFind(int n) {
    count_ = n;
    parent_.resize(n);
    for (int i = 0; i < n; ++i) {
      parent_[i] = i;  // 自己为自己的父节点
    }
  }
  // 并
  void Union(int point1, int point2) {
    int f1 = Find(point1);
    int f2 = Find(point2);
    if (f1 == f2) return;  // 根节点相同，已经在一个图中了
    parent_[f1] = f2;  // f1（point1的祖先） 的父节点设为 f2（point2的祖先）
  }
  // 查
  // int Find(int point) {
  //   // 如果父节点不是自己，则一直向上找到根节点
  //   while (parent_[point] != point) {
  //     parent_[point] = parent_[parent_[point]];
  //     point = parent_[point];
  //   }
  //   return parent_[point];
  // }

  // 查 递归
  // int Find(int point) {
  //   if (parent_[point] == point)
  //     return point;
  //   else
  //     return find(parent_[point]);
  // }
  // 如果根节点为同一个，则是连通的

  // 查 递归
  int Find(int i) {
    if (parent_[i] == i)
      return i;
    else {
      // 路径压缩
      parent_[i] = Find(parent_[i]);
      return parent_[i];
    }
  }
  // 如果根节点为同一个，则是连通的
  bool Connected(int point1, int point2) {
    return Find(point1) == Find(point2);
  }

 private:
  int count_;
  std::vector<int> parent_;
};

struct Edge {
  int p1_;
  int p2_;
  int manhattan_;
  Edge(int p1, int p2, int manhattan)
      : p1_(p1), p2_(p2), manhattan_(manhattan) {}
};

class Solution {
 public:
  int minCostConnectPoints(vector<vector<int>>& points) {
    int points_size = points.size();
    UnionFind union_find(points_size);

    std::vector<Edge> edges;
    for (int i = 0; i < points_size; ++i) {
      for (int j = i + 1; j < points_size; ++j) {
        int i_x = points[i][0];
        int i_y = points[i][1];
        int j_x = points[j][0];
        int j_y = points[j][1];
        int manhattan = std::abs(i_x - j_x) + std::abs(i_y - j_y);
        edges.emplace_back(i, j, manhattan);
      }
    }
    // 若是最大生成树，把这里的 ‘<’ 改为 ‘>’ 即可
    std::sort(edges.begin(), edges.end(),
              [&](Edge& a, Edge& b) { return a.manhattan_ < b.manhattan_; });

    int res_mst = 0;
    // 贪心选择
    for (auto edge : edges) {
      int point1 = edge.p1_;
      int point2 = edge.p2_;
      int distance = edge.manhattan_;
      if (union_find.Connected(point1, point2)) continue;
      res_mst += distance;
      union_find.Union(point1, point2);
    }

    return res_mst;
  }
};
// @lc code=end
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110

• Kruskal 算法以边为单元，时间 $O(mlog(m))$ 主要取决于边数，比较适合于稀疏图.

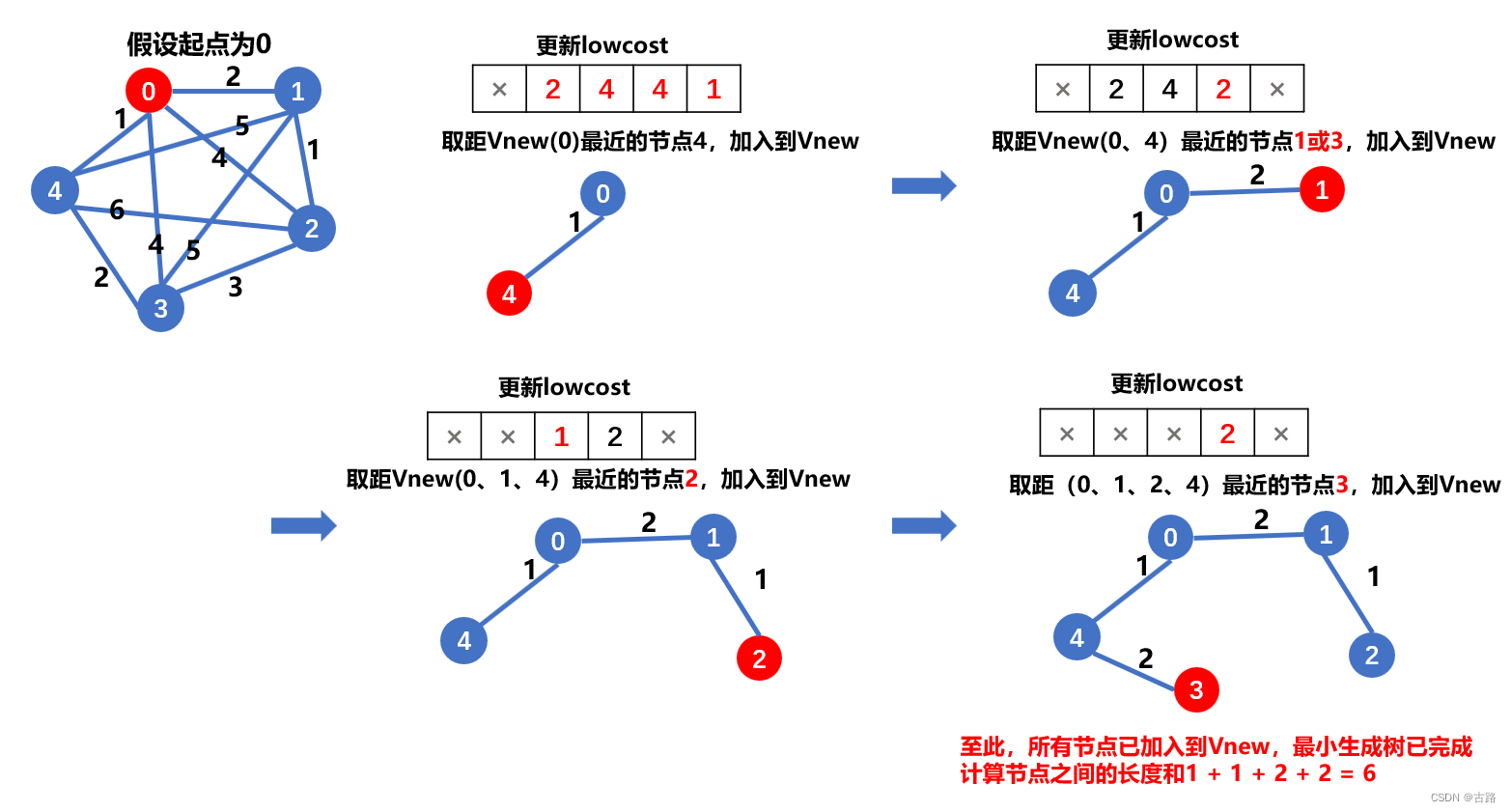
2.Prim算法

prim 算法其实就是 BFS 思想。

/*
 * @Date: 2022-06-30
 * @Author: bFeng
 */
/*
 * @lc app=leetcode.cn id=1584 lang=cpp
 *
 * [1584] 连接所有点的最小费用
 */

// @lc code=start
struct Edge {
  int p1_;
  int p2_;
  int manhattan_;
  Edge(int p1, int p2, int manhattan)
      : p1_(p1), p2_(p2), manhattan_(manhattan) {}
};

// 注意优先队列 class Compare = std::less<typename Container::value_type>
// less 时是最大堆
// 若要构建最大生成树，把此处的 ‘>’ 改为 '<'
struct Cmp {
  bool operator()(Edge& a, Edge& b) { return a.manhattan_ > b.manhattan_; }
};

class Solution {
 public:
  int minCostConnectPoints(vector<vector<int>>& points) {
    int points_size = points.size(); // 示例1： points_size = 5
    visited_.resize(points_size);
    // 自上而下，自左到右 对节点编号 0 1 2 3 4
    // 邻接表
    // graph[0]: (p1, w01),(p2, w02),(p3, w03),(p4, w04)
    // graph[1]: (p2, w12),(p3, w13),(p4, w14)
    // graph[2]: (p3, w23),(p4, w24)
    // graph[3]: (p4, w34)
    // graph[4]: 
    std::vector<std::vector<pair<int, int>>> graph(points_size);

    for (int i = 0; i < points_size; ++i) {
      for (int j = i + 1; j < points_size; ++j) {
        int i_x = points[i][0];
        int i_y = points[i][1];
        int j_x = points[j][0];
        int j_y = points[j][1];
        int manhattan = std::abs(i_x - j_x) + std::abs(i_y - j_y);
        graph[i].push_back({j, manhattan});
        graph[j].push_back({i, manhattan});
      }
    }

    int res_mst = 0;
    visited_[0] = true;
    cut(0, graph);
    // 贪心选择
    while(!edge_queue_.empty()) {
      // 取出这一列表中最小权重的边
      Edge edge = edge_queue_.top();
      edge_queue_.pop();
      int to_point = edge.p2_;
      int weight = edge.manhattan_;
      if (visited_[to_point]) continue;
      res_mst += weight;
      visited_[to_point] = true;
      // BFS
      cut(to_point, graph);
    }

    return res_mst;
  }

  private:
  std::priority_queue<Edge, std::vector<Edge>, Cmp> edge_queue_; //
  std::vector<bool> visited_ = {false};
  void cut(int point, std::vector<std::vector<std::pair<int,int>>>& graph) {
    for (auto& p : graph[point]) { // 遍历一个表,构建边并排序
      int to_point = p.first;
      int weight = p.second;
      if (visited_[to_point]) continue;
      edge_queue_.push({point, to_point, weight});
    }
  }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84

注意优先队列的 cmp ,有点反直觉啊。

• 时间复杂度 $O(n^2)$, 适合稠密图