数据结构中重要的排序算法

1. 直接插入、冒泡和简单选择是最基本的，思想容易理解，代码实现也简单，适合元素个数n不是很大（n<1000）的情况；时间复杂度都是$O(n)$，简单选择不稳定；
2. 希尔排序对于中等规模（n<=1000)的比较好。不需要额外内存，但不稳定；
3. 对于元素个数n很大的情况，可采用快排、堆排序、归并排序或基数排序，其中快排和堆排序都是不稳定的；
4. 快排是最通用的高效内部算法；堆也高效，不需要额外空间，但堆不大可能提供比快速排序更好的平均性能；归并排序一个重要特性是与序列初始状态无关，缺点是需要额外$O(n)$的存储空间(用不了这么多)；基数排序比较特殊，对关键字各位大小进行比较，需要额外空间。
5. 平均时间度为$O(n{\log }_{2}n)$的稳定排序算法只有归并排序，对于判断稳定的排序方法，举个不稳定的例子就能知道稳不稳定；
6. 若序列初始基本有序，则选用直接插入或冒泡排序为宜；快速排序对于有序或逆序的慢，快的是划分均匀。

本篇文章篇幅较长，我是为了考研写的，很多都是借鉴王道上的，初学者也可以看，都是排序基础算法；
每节内容有，排序思想、性能分析、代码实现、往年408出题等吧

这里代码应该都是以增序（、从小到大）（、顺序）排序；
代码都带有注释；
代码参考了王道上和当年学数据结构这门课写的代码， 再加上现在的风格；
最后给个各种排序算法时间的比较。

插入排序

算法思想：每次将一个待排序的记录按其关键字大小插入到前面已排好序的子序列中，直到全部记录插入完成。
即：从头往后，设定一个“指针”（第二个数），依次比较前面的大小，放到合适的位置（可以使用哨兵，A[0]存放待插元素）

• 时间复杂度：$O(n^2)$
  

直接插入排序

• 时间复杂度：$O(n^2)$
• 稳定
• 适用于顺序存储和链式存储的线性表，为链式存储时，可以从前往后查找指定元素位置。
• 最好时间复杂度：$O(n)$，原本有序；最坏时间复杂度：$O(n^2)$，原本逆序

代码：

//直接插入排序
void InsertSort(int A[], int n){
	int i,j,temp;
	for(i=1;i<n;i++){
		if(A[i] < A[i-1]){		//A[i]小于前面的，需要往前移动 
			temp = A[i];
			for(j=i-1;j>=0 && A[j]>temp;j--)		//找到A[i]移动我位置 
				A[j+1] = A[j];
			A[j+1] = temp;		//将暂存的A[i]插入位置 
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12

带哨兵的示例：

一趟结果：前面几个元素是有序的
第一趟：前两个有序（38，49）；
第二趟：前三个有序（38，49，65）；
。。。

---

折半插入排序

A[i]元素前面已经是有序的，使用折半查找找到插入位置可以减少比较元素的次数，移动次数未改变。

• 时间复杂度：$O(n^2)$
• 稳定
• 仅适用顺序表
• 最好时间复杂度：$O(n)$，有序；最坏时间复杂度：$O(n^2)$，逆序

带哨兵的折半插入代码：

---

希尔排序

（代码）思想：希尔排序按照增量（步长）划分元素组，然后对每个元素组用插入排序调整顺序，为一趟，然后减少增量，再对每个元素组排序，直到增量d=1为止。希尔排序属于插入排序。

• 时间的复杂度：和增量序列$d_i,d_2,d_3,...$的选择有关，最坏时间复杂度为$O(n^2)$，当n在某个范围内时，可达$O(n^{1.3})$
• 不稳定
• 仅适用于顺序表，不适用于链表
  
  
  一趟结果：元素组（局部，间隔增量的元素）有序
  以上图为例，第一趟（增量5）：第1、6有序，第2，7有序，。。。
  第二趟（增量3）：第1、4、7、10有序，。。。
  。。。

代码：

//希尔排序
void ShellSort(int A[], int n){
	int i,j,temp;
	int d;		//步长
	for(d=n/2; d>=1; d=d/2){		//步长变化 
		for(i=d; i<n; i++){		//对多有相隔d位置的所有元素组进行直接插入排序 
			temp = A[i];
			for(j=i-d; j>=0 && temp<A[j]; j-=d){	//对相隔d位置的元素进行直接插入排序 
				A[j+d] = A[j];		//记录后移，查找插入位置 
			}
			A[j+d] = temp;		//插入
		}
	}
} 
1
2
3
4
5
6
7
8
9
10
11
12
13
14

这还有一个带哨兵的希尔排序，这里两个“相隔”的元素操作后，切换到下一个元素组，而不是像上面的把整个元素组排序好再下一个；

出题，408里算是出过两种类型的：
一种是给你一个序列，让判断是用哪种排序算法得到的
第二种是对于希尔排序，给出一个序列，让判断增量是多少，这种出现过两次。

---

交换排序

基于“交换”的排序：根据序列中两个元素关键字的比较结果来对换这两个记录在序列中的位置。
有冒泡排序（冒泡）和快速排序（快排）。

冒泡排序

思想：从后往前（或者从前往后），两两比较相邻的元素的值，两两交换，把最小的放到最前面，依次这样，实现从小到大（顺序）。

一趟结果，最小（最大）的提到最前面。

• 时间复杂度 $O(n^2)$
• 稳定
• 适用性：顺序表、链表都可
• 最好时间复杂度：$O(n)$，有序；最坏：$O(n^2)$，逆序
  

代码（这个是单向的，最后完整代码里还有个双向冒泡，快了那么一点点）：

//交换 
void swap(int &a, int &b){
	int temp = a;
	a = b;
	b = temp;
} 

//冒泡排序
void BubbleSort(int A[], int n){
	int i,j;
	bool flag = false;		//表本趟是否发生交换的标志 
	for(i=0;i<n-1;i++){
		flag = false;
		for(j=n-1;j>i;j--){			//一趟冒泡 
			if(A[j-1]>A[j]){		//小的放前面 
				swap(A[j-1],A[j]);		//交换 
				flag = true;
			}
		}
		if(flag == false)
			return;			//本趟没有发生交换，说明已经有序了，提前结束 
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

---

快速排序

思想：选取一个元素作为基准pivot（一般第一个元素），设置两个指针low（从前往后）和high（从后往前），把所有小于基准的元素放到左面，所有大于pivot的元素放到右边，这样pivot是放在最终位置，实现增序排序，然后再递归的对两个子表重复以上操作，直至每部分只有一个元素或为空为止。

快速排序性能分析：

• 时间复杂度：$O(n{\log }_{2}n)$

• 不稳定

• 空间效率：快速排序是递归的，需要借助递归工作栈，最好情况下为$O({\log }_{2}n)$；最坏情况下，因为需要进行n-1次递归调用，所以栈的深度为$O(n)$；平均情况下，栈的深度为$O({\log }_{2}n)$。

• 时间效率：当每次的基准把表等分为长度相近的两个子表时，速度是最快的，为$O(n{\log }_{2}n)$；
  当表本身已经有序或逆序时，速度最慢，这样最坏情况时间复杂度为$O(n^2)$。

一趟“划分”：确定一个元素的最终位置，前面的都小于基准值，后面的都大于。
一“趟”定义：（在408），排序过程中，对尚未确定最终位置的所有元素进行一遍处理称为一“趟”。一次“划分”可以确定一个元素的最终位置，而一趟排序也许可以确定多个元素的位置，看下面这个例子：

第一趟确定了49的位置；第二趟紧接着处理上次划分的左右区间，确定左区间27的位置，右区间76的位置，第二趟确定的两个元素的最终位置；然后第三趟，上次划分的区间右四个，要确定四个元素的位置，如上图四三层。

粘个王道上的：

代码实现：

//快速排序
//用第一个元素作为基准将序列划分为左右两部分 
int Partition(int A[],int low,int high){
	int pivot = A[low];		//第一个元素作为基准
	while(low < high){
		while(low<high && A[high]>=pivot) high--;
		A[low] = A[high];	//low位置的元素取出来了（pivot），可以直接放
		while(low<high && A[low]<=pivot) low++;
		A[high] = A[low]; 
	} 
	A[low] = pivot;		//基准pivot放到最终位置
	return low; 		//返回存放基准的最终位置，为了划分左右子表 
}
//快排 
void QuickSort(int A[],int low,int high){
	if(low<high){
		int pivotpos = Partition(A,low,high);	//确定一个基准
		QuickSort(A,low,pivotpos-1);		//对左子表划分 
		QuickSort(A,pivotpos+1,high);		//对右区间划分，对左右分区处理顺序可以交换（无所谓、不碍事）
	}
} 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

出题：

【9.分析】：当分得两个相近的子表时，速度最快；表本来就是顺序或逆序时，速度最慢；
题目不说以谁为基准，就用第一个元素当每趟的基准，下面是第一趟划分后的序列：
对选项A， { 9 , 17 , 5 } , 21 , { 25 , 23 , 30 } \{ 9,17,5 \}, 21, \{ 25,23,30 \} {9,17,5},21,{25,23,30}
对B， { 1 , 5 , 21 , 17 } , 25 , { 30 , 23 } \{1,5,21,17 \}, 25, \{ 30,23 \} {1,5,21,17},25,{30,23}
对C， { 5 , 9 , 17 } , 21 , { 30 , 25 , 23 } \{ 5,9,17 \}, 21, \{30,25,23 \} {5,9,17},21,{30,25,23}
对选项D，D中的序列时有序的，因此是最慢的；
从中可以看出，A和C中划分的最“平均”（等分），然后再看子表，A中左子表再次划分为： { 5 } , 9 , { 17 } \{ 5 \}, 9, \{ 17 \} {5},9,{17}，是等分的；选项C左右子表不等分；因此最快的是A。

看下17题，【分析】，做这类题，可以写出最终排序好的序列，对照有几个确定最终位置的。
注意，一趟指的是对所有元素进行一遍处理，怎么说呢，先看下对照表：

四个选项中，都有两个确定最终位置的；在第一趟中，一般是确定一个位置；第二趟，要将第一趟划分的左右区间都确定个元素的最终位置，所以说第二趟后至少有一个元素在边界（第二趟结束后有两个确定的），这样就能保证第二趟左右区间都划分了。
看下选项A，先确定72；第二趟，左区间确定28，没有右区间，故第二趟结束可以是这样，对；选项B和C同样的道理；
来看选项D，若先确定12；第二趟对12的左区间和右区间都进行“划分”，可以明显看到左区间没划分，得有一个位置是对头的才行。

---

选择排序

选择排序：每一趟在待排序元素中选取关键字最小（或最大）的元素加入有序子序列，重点是堆排序。

简单选择排序

思想：每一趟找到最小的元素放到最前面（与前面的交换）（顺序）

• 时间复杂度：$O(n^2)$，简单选择排序算法比较次数始终都是$n(n-1)/2$，与序列状态无关。
• 稳定性：不稳定
  

代码：

//简单选择排序
void SelectSort(int A[], int n){
	int i,j,min;
	for(i=0;i<n-1;i++){		//共进行n-1趟 
		min = i;		//min存放最元素下标 
		for(j=i+1;j<n;j++){
			if(A[j] < A[min]) min=j; 
		}
		if(min != i) swap(A[i],A[min]);			//交换最小的放到前面 
	}
} 
1
2
3
4
5
6
7
8
9
10
11

---

堆排序

堆定义：
①$L(i)\ge L(2i)且L(i)\ge L(2i+1)$，大根堆：$根\ge 左、右$
②或$L(i)\le L(2i)且L(i)\le L(2i+1)$，小根堆：$根\le 左、右$
使用大根堆排序，得到的是递增序列，从小到大；排序过程中，堆顶（最大）元素，与最下面的交换，最大的元素确定到最后；
同理，使用小根堆得到的是递减序列。

堆排序思路：首先将n个元素建成初始堆，堆顶就是最大值，将堆顶元素与待排序列中最后一个元素交换，默认为移除大根堆，此时堆被破坏，将堆顶元素继续向下调整使其继续保持大顶堆的性质（小元素下坠），这是第一趟处理。再次输出堆顶，如此反复，直到堆中仅剩一个元素为止。

• 时间复杂度$O(n{\log }_{2}n)$，建堆时间为$O(n)$；有n-1次向下调整操作每次调整时间复杂度为$O(n)$，在最好最坏的情况下，堆排序的时间复杂度都为$O(n{\log }_{2}n)$
• 不稳定

插入和删除，插入和删除一个元素的时间复杂度都为$O({\log }_{2}n)$

代码思想：
可以直接看代码，都有注释，这里大白话多，
建立大根堆得到的是递增序列；①调整一个大根堆HeadAdjust()，让其根节点不断“下坠”，遇到比它大的数就换下去，直到叶子结点，若中途没有比它大的就结束循环；
②然后初建堆，以分支节点$\lfloor n/2\rfloor$从后往前依次调整（根也要）；
③建立好初始大根堆，开始堆排，堆顶为最大元素，让其与堆底元素交换，这样确定了最大的元素位置（符合选择排序，找到最大的元素）；堆底跑最上面了，就要调整大根堆，让其不断下坠，最大的再上来。

代码，加了哨兵，下标从1开始，因为这样比较好找儿子结点：

//堆排序，大根堆=>递增序列 
//以k为根，调整大根堆
void HeadAdjust(int A[], int k, int n){
	//调整k为根的子树，不断下坠，让大的上来 
	int i;
	A[0] = A[k];			//A[0]暂存子树根结点（k） 
	for(i=k*2;i<=n;i*=2){	//不断下坠 
		if(i<n && A[i]<A[i+1])
			i++;			//在儿子结点挑选最大的
		if(A[0]>=A[i])
			break;			//A[0]根最大，不用下坠，直接结束 
		else{
			A[k] = A[i];		//将A[i]调整到双亲上， 
			k = i;				//修改k的值，让其最为根，继续下坠 
		}
	}
	A[k] = A[0]; 
}
//循环建立小根堆 
void BuildMinHeap(int A[],int n){
	for(int i=n/2;i>=1;i--)		//非叶子结点（分支结点）从后往前调整 
		HeadAdjust(A,i,n);
} 
//堆排 
void HeapSort(int A[], int n){
	BuildMinHeap(A,n);		//初始堆 
	for(int i=n;i>1;i--){		//n-1趟交换和键堆过程 
		swap(A[i],A[1]);		//堆顶（最小）元素与堆低元素交换
		HeadAdjust(A,1,i-1); 	//把剩下待排序列整理成小根堆 
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

出题，堆在408中出现的蛮多的，要熟练掌握对堆的建立和插入

【解析】


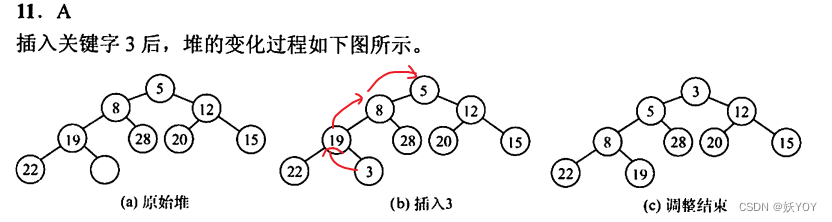
【14题】，C，删除8后，最后（尾）的12放到顶端，然后下坠，然后计算比较次数就行了，注意不交换位的比较也算上。

【17题】B，注意题目说的是要从零开始建堆

---

归并排序

归并：把两个或多个已经有序的序列合并成一个

二路归并性能分析：

• 空间复杂度：$O(n)$，辅助数组
• 时间复杂度：$O(n{\log }_{2}n)$，与序列初始状态无关
• 稳定

二路归并示例：

二叉树的第h层最多有$2^{h-1}$个结点，若树高为h，则应满足$n\le 2^{h-1}$，即$h-1=\lceil {\log }_{2}n\rceil$
结论：n个元素进行二路归并排序，归并趟数=$\lceil {\log }_{2}n\rceil$，每趟归并时间复杂度为$O(n)$，算法时间复杂度为$O(n{\log }_{2}n)$

代码思想：需要一个辅助数组，将待归并的子序列A[low…mid…high]，先都复制到B中，设置三个指针i=low,j=mid+1,k=low（如下图），i、j往后移，依次将小的放到A[k]中，这样就实现了两个有序数组合并。这个辅助数组设置的其实有点大，可以仅分配待合并序列的长度，这样的话就需要，在A中元素根据指针依次放到B中，在最后完整代码里是这样思路（我比较喜欢这种，下面代码是采用的王道的）。

代码：

#define MaxSize 1001
//二路归并排序 
int *B = new int[MaxSize];
//A[low...mid]和A[mid+1...high]各自有序，将两个部分归并 
void Merge(int A[],int low,int mid,int high){
	int i,j,k;
	for(k=low;k<=high;k++)
		B[k] = A[k];		//将A中所有元素复制到B中
	for(i=low,j=mid+1,k=i; i<=mid&&j<=high; k++){
		if(B[i]<=B[j])		//把小的元素放到A中 
			A[k] = B[i++];
		else
			A[k] = B[j++];
	}
	while(i<=mid) A[k++] = B[i++];		//左表有剩余，全部放到A后面
	while(j<=high) A[k++] = B[j++];
}
void MergeSort(int A[],int low,int high){
	if(low < high){
		int mid = (low+high)/2;			//中间划分
		MergeSort(A,low,mid);			//对左半部分归并排序
		MergeSort(A,mid+1,high);		//对后半部分归并排序
		Merge(A,low,mid,high);			//归并	
	}
} 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

---

基数排序

不基于比较和移动进行排序，而是基于关键字各位的大小进行排序。
通常用最低位优先（LSD）法，越往后面的“权重越大”，得到递减有序序列。

性能分析：

• 空间复杂度：$O(r)$
• 时间复杂度$O(d(n+r))$，d趟收集和分配，与序列初始状态无关
• 稳定

基数排序擅长解决的问题：
①数据元素的关键字可以方便的拆分为d组，且d较小；例如将学生信息按年龄排序（年月日）（反例：给五个人的身份证号排序，n小d大）
②每组关键字的取值范围不大，即r较小（反例：给中文人名排序，r大，姓氏太多了）
③数据元素个数n较大

基数排序，数据结构形状：

排序过程：

每趟得到的序列：

习题（408有两个基数排序的题，没有归并的有关排序序列的题，感觉23年会有）：


【分析】

14题：C，其实这个直接看就行，第一趟372相邻的，就找个位是1、2和3的，排这三个就行了，其他的不看。

---

外部排序

这部分当时上数据结构课的没有讲好像，408中出题不多。可以选择性的看。
归并趟数$S=\lceil {\log }_{k}r\rceil$，k是归并趟数，r是初始归并段数量。

样子：

败者树
归并趟数$S=\lceil {\log }_{k}r\rceil$，
增加归并路数k，以减少归并趟数S，进而减少I/O次数，但内部归并时间将增加，因此为使内部归并不受k影响，引入败者树（可视为完全二叉树，多了个头头）。
有了败者树，只需对比关键字$\lceil {\log }_{2}k\rceil$次，就能选取最小元素，传统是n-1次

置换-选择排序
用于生成外部排序的初始归并段
归并趟数$S=\lceil {\log }_{k}r\rceil$，减小初始归并段个数r，操作系统里面也有个页面置换算法。

最佳归并树
文件经置换-选择排序后，得到的是长度不等的初始归并段；讨论的就是如何组织长度不等的初始归并段的归并排序，类似哈夫曼树推广到m叉树【带权路径长度(WPL)最小的二叉树成为哈夫曼树】

【注意】：对于k叉归并，要是初始归并段的数量为u发构成严格的k叉归并数，则需要补充几个长度为0的“虚段”，再进行k叉哈夫曼树的构造。
①若(初始归并段数-1) % (k-1) = 0，说明刚好可以构成严格k叉树
②若(初始归并段数-1) % (k-1) = u ≠ 0，则需要补充 (k-1) - u个虚段

出题：

【析】若(初始归并段数-1) % (k-1) = u ≠ 0，则需要补充 (k-1) - u个虚段

---

完整代码（各时间对比）

#include<iostream>
using namespace std;
#include <stdlib.h>
#include <sys/timeb.h>
#include <time.h>

#define MaxSize 50001
typedef int KeyType;

void initial(int R[],int low,int high)	//产生R[low..high]中的随机数
{
	int i;
	srand((unsigned)time(NULL));		//随机种子，使得每次生成随机数不同 
	for (i=low;i<=high;i++)
		R[i]=rand()%50000+1;		//范围[1,50000]的数 
}
bool test(KeyType R[],int low,int high)	//验证排序结果的正确性，递增序列
{
	int i;
	for (i=low;i<=high-1;i++)
		if (R[i]>R[i+1])
			return false;
	return true;
}
void Difference(struct _timeb timebuf1,struct _timeb timebuf2)	//求时间差
{
	long s,ms;
	s=timebuf2.time-timebuf1.time;			//两时间相差的秒数
	ms=timebuf2.millitm-timebuf1.millitm;	//两时间相差的毫秒数
	if (ms<0)
	{
		s--;
		ms=1000+ms;
	}
	printf("%d秒%d毫秒",s,ms);
}
//交换两个数 
void swap(int &a,int &b){
	int tmp = a;
	a = b;
	b = tmp;
}
//-------直接插入排序----------
void InsertSort(KeyType R[],int n)
{
	int i,j;
	KeyType tmp;
	for (i=1;i<n;i++)
	{
		tmp=R[i];
		j=i-1;				//从右向左在有序区R[0..i-1]中找R[i]的插入位置
		while (j>=0 && tmp<R[j])
		{	R[j+1]=R[j];	//将关键字大于R[i]的元素后移
			j--;
		}
		R[j+1]=tmp;			//在j+1处插入R[i]
	}
}
void InsertSortTime()		//求直接插入排序的时间
{
	KeyType R[MaxSize];
	int n=50000;
	struct _timeb timebuf1,timebuf2;
	printf("直接插入排序\t");
	initial(R,0,n-1);		//R[0,...n-1] 
	_ftime(&timebuf1);
	InsertSort(R,n);
	_ftime(&timebuf2);
	Difference(timebuf1,timebuf2);
	if (test(R,0,n-1))
		printf("\t正确\n");
	else
		printf("\t错误\n");
}
//------折半插入排序----------
void InsertSort1(KeyType R[],int n)
{
	int i,j,low,high,mid;
	int tmp;
	for (i=1;i<n;i++)
	{
		tmp=R[i];					//将R[i]保存到tmp中
		low=0;high=i-1;
		while (low<=high)			//在R[low..high]中折半查找有序插入的位置
		{
			mid=(low+high)/2;		//取中间位置
			if (tmp<R[mid])
				high=mid-1;			//插入点在左半区
			else
				low=mid+1;			//插入点在右半区
		}
		for (j=i-1;j>=high+1;j--)	//元素后移
			R[j+1]=R[j];
		R[high+1]=tmp;				//插入
	}
}
void InsertSort1Time()		//求折半插入排序的时间
{
	KeyType R[MaxSize];
	int n=50000;
	struct _timeb timebuf1,timebuf2;
	printf("折半插入排序\t");
	initial(R,0,n-1);
	_ftime(&timebuf1);
	InsertSort1(R,n);
	_ftime(&timebuf2);
	Difference(timebuf1,timebuf2);
	if (test(R,0,n-1))
		printf("\t正确\n");
	else
		printf("\t错误\n");
}
//-----------希尔排序算法--------------
void ShellSort(KeyType R[],int n)
{
	int i,j,gap;
	KeyType tmp;
	gap=n/2;				//增量置初值
	while (gap>0)
	{	for (i=gap;i<n;i++) //对所有相隔gap位置的所有元素组采用直接插入排序
		{	tmp=R[i];
			j=i-gap;
			while (j>=0 && tmp<R[j])//对相隔gap位置的元素组进行排序
			{	R[j+gap]=R[j];
				j=j-gap;
			}
			R[j+gap]=tmp;
		}
		gap=gap/2;	//减小增量
	}
}
void ShellSortTime()		//求希尔排序算法的时间
{
	KeyType R[MaxSize];
	int n=50000;
	struct _timeb timebuf1,timebuf2;
	printf("希尔排序\t");
	initial(R,0,n-1);
	_ftime(&timebuf1);
	ShellSort(R,n);
	_ftime(&timebuf2);
	Difference(timebuf1,timebuf2);
	if (test(R,0,n-1))
		printf("\t正确\n");
	else
		printf("\t错误\n");
}
//--------冒泡排序算法----------
void BubbleSort(KeyType R[],int n)
{
	int i,j;
	bool exchange;
	KeyType tmp;
	for (i=0;i<n-1;i++) 
	{
		exchange=false;
		for (j=0;j<n-i-1;j++)	//比较,找出最大关键字的元素
			if (R[j]>R[j+1])
			{	swap(R[j],R[j+1]);		//R[j]与R[j+1]进行交换,将最大关键字元素前移
				exchange=true;
			}
		if (!exchange)		//本趟没有发生交换，中途结束算法
			return;
	}
}
void BubbleSortTime()		//求冒泡排序算法的时间
{
	KeyType R[MaxSize];
	int n=50000;
	struct _timeb timebuf1,timebuf2;
	printf("冒泡排序\t");
	initial(R,0,n-1);
	_ftime(&timebuf1);
	BubbleSort(R,n);
	_ftime(&timebuf2);
	Difference(timebuf1,timebuf2);
	if (test(R,0,n-1))
		printf("\t正确\n");
	else
		printf("\t错误\n");
}
//--------双向冒泡排序算法----------
void dBubbleSort(KeyType R[],int n){
	int i=0,j=n-1,k;
	KeyType tmp;
	bool exchange;			//没有发生交换的判定，可加可不加 
	while(i<j){
		exchange = false;
		for(k=i;k<j;k++){
			if(R[k]>R[k+1]){
				swap(R[k],R[k+1]);
				exchange = true;
			}
		}
		j--;			//最后一位已经是最大值，即尾标记可往前移一位 
		for(k=j;k>i;k--){
			if(R[k-1]>R[k]){
				swap(R[k],R[k-1]);
				exchange = true;
			}
		}
		i++;
		if(!exchange) return;
	}
}
void dBubbleSortTime()		//求双向冒泡排序算法的时间
{
	KeyType R[MaxSize];
	int n=50000;
	struct _timeb timebuf1,timebuf2;
	printf("双向冒泡排序\t");
	initial(R,0,n-1);
	_ftime(&timebuf1);
	dBubbleSort(R,n);
	_ftime(&timebuf2);
	Difference(timebuf1,timebuf2);
	if (test(R,0,n-1))
		printf("\t正确\n");
	else
		printf("\t错误\n");
}
	
//--------快速排序算法---------------
void QuickSort(KeyType R[],int s,int t)
{
	int i=s,j=t;
	KeyType tmp;
	if (s<t) 				//区间内至少存在两个元素的情况
	{
		tmp=R[s];			//用区间的第1个元素作为基准
		while (i!=j)		//从区间两端交替向中间扫描,直至i=j为止
		{
			while (j>i && R[j]>=tmp) 
				j--;		//从右向左扫描,找第1个小于tmp的R[j]
			R[i]=R[j];		//找到这样的R[j],R[i]和R[j]交换
			while (i<j && R[i]<=tmp) 
				i++;		//从左向右扫描,找第1个大于tmp的元素R[i]
			R[j]=R[i];		//找到这样的R[i],R[i]和R[j]交换
		}
		R[i]=tmp;
		QuickSort(R,s,i-1);	//对左区间递归排序
		QuickSort(R,i+1,t);	//对右区间递归排序
	}
}
void QuickSortTime()		//求快速排序算法的时间
{
	KeyType R[MaxSize];
	int n=50000;
	struct _timeb timebuf1,timebuf2;
	printf("快速排序\t");
	initial(R,0,n-1);
	_ftime(&timebuf1);
	QuickSort(R,0,n-1);
	_ftime(&timebuf2);
	Difference(timebuf1,timebuf2);
	if (test(R,0,n-1))
		printf("\t正确\n");
	else
		printf("\t错误\n");
}
//---------直接选择排序---------
void SelectSort(KeyType R[],int n)
{	int i,j,k;
	KeyType tmp;
	for (i=0;i<n-1;i++)			//做第i趟排序
	{	k=i;
		for (j=i+1;j<n;j++)		//在当前无序区R[i..n-1]中选key最小的R[k]
			if (R[j]<R[k])
				k=j;			//k记下目前找到的最小关键字所在的位置
		if (k!=i)				//交换R[i]和R[k]
			swap(R[i],R[k]);
	}
}
void SelectSortTime()		//求直接选择排序算法的时间
{
	KeyType R[MaxSize];
	int n=50000;
	struct _timeb timebuf1,timebuf2;
	printf("直接选择排序\t");
	initial(R,0,n-1);
	_ftime(&timebuf1);
	SelectSort(R,n);
	_ftime(&timebuf2);
	Difference(timebuf1,timebuf2);
	if (test(R,0,n-1))
		printf("\t正确\n");
	else
		printf("\t错误\n");
}
//----------堆排序算法----------
void sift(KeyType R[],int low,int high)
{	
	int i=low,j=2*i;						//i为根，R[j]是R[i]的左孩子
	KeyType tmp=R[i];
	while (j<=high)
	{	if (j<high && R[j]<R[j+1]) 	//若右孩子较大,把j指向右孩子
			j++;
		if (tmp<R[j]) 
		{	R[i]=R[j];						//将R[j]调整到双亲节点位置上
			i=j;							//修改i和j值,以便继续向下筛选
			j=2*i;
		}
		else break;							//筛选结束
	}
	R[i]=tmp;								//被筛选节点的值放入最终位置
}
void HeapSort(KeyType R[],int n)
{
	int i;
	KeyType tmp;
	for (i=n/2;i>=1;i--)	//循环建立初始大根堆
		sift(R,i,n); 
	for (i=n;i>=2;i--)		//进行n-1趟完成推排序,每一趟堆排序的元素个数减1
	{
		swap(R[i],R[1]);	//将最后一个元素同当前区间内R[1]对换
		sift(R,1,i-1);		//筛选R[1]节点,得到i-1个节点的堆
	}
}
void HeapSortTime()			//求堆排序算法的时间
{
	KeyType R[MaxSize];
	int n=50000;
	struct _timeb timebuf1,timebuf2;
	printf("堆 排 序\t");
	initial(R,1,n);			//A[1,...,n]
	_ftime(&timebuf1);
	HeapSort(R,n);
	_ftime(&timebuf2);
	Difference(timebuf1,timebuf2);
	if (test(R,1,n))
		printf("\t正确\n");
	else
		printf("\t错误\n");
}
//--------二路归并排序算法------------
void Merge(KeyType R[],int low,int mid,int high) 
{
	KeyType *R1;
	int i=low,j=mid+1,k=0; //k是R1的下标,i、j分别为第1、2段的下标
	R1=(KeyType *)malloc((high-low+1)*sizeof(KeyType));  //动态分配空间
	while (i<=mid && j<=high)		//在第1段和第2段均未扫描完时循环
		if (R[i]<=R[j])		//将第1段中的元素放入R1中
		{	R1[k]=R[i];
			i++;k++;
		}
		else						//将第2段中的元素放入R1中
		{	R1[k]=R[j];
			j++;k++; 
		}
	while (i<=mid)					//将第1段余下部分复制到R1
	{	R1[k]=R[i];
		i++;k++;
	}
	while (j<=high)					//将第2段余下部分复制到R1
	{	R1[k]=R[j];
		j++;k++;
	}
	for (k=0,i=low;i<=high;k++,i++) //将R1复制回R中
		R[i]=R1[k];
	free(R1);
}
void MergePass(KeyType R[],int length,int n)	//对整个数序进行一趟归并
{	int i;
	for (i=0;i+2*length-1<n;i=i+2*length)	//归并length长的两相邻子表
		Merge(R,i,i+length-1,i+2*length-1);
	if (i+length-1<n)					//余下两个子表,后者长度小于length
		Merge(R,i,i+length-1,n-1);		//归并这两个子表
}
void MergeSort(KeyType R[],int n)	//自底向上的二路归并算法
{	int length;
	for (length=1;length<n;length=2*length)//进行log2n趟归并
		MergePass(R,length,n);
}
void MergeSortTime()			//求二路归并排序算法的时间
{
	KeyType R[MaxSize];
	int n=50000;
	struct _timeb timebuf1,timebuf2;
	printf("二路归并排序\t");
	initial(R,0,n-1);
	_ftime(&timebuf1);
	MergeSort(R,n);
	_ftime(&timebuf2);
	Difference(timebuf1,timebuf2);
	if (test(R,0,n-1))
		printf("\t正确\n");
	else
		printf("\t错误\n");
}
int main()
{
	printf("随机产生50000个1-50000的正整数,各种排序方法的比较\n");
	printf("------------------------------------------------\n");
	printf("排序方法         用时         结果验证\n");
	printf("------------------------------------------------\n");
	InsertSortTime();		//直接插入排序 
	InsertSort1Time();		//折半插入排序 
	ShellSortTime();		//希尔排序 
	BubbleSortTime();		//冒泡排序 
	dBubbleSortTime();	 	//双向冒泡排序 
	QuickSortTime();		//快速排序 
	SelectSortTime();		//选择排序 
	HeapSortTime();			//堆排序 
	MergeSortTime();		//合并排序 
	printf("------------------------------------------------\n");
return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407

运行结果：