1 原始链接

https://www.boost.org/doc/libs/1_55_0/libs/numeric/odeint/doc/html/boost_numeric_odeint/tutorial/using_cuda__or_openmp__tbb_______via_thrust.html

---

2 简介（小规模问题不要用GPU）

Modern graphic cards (graphic processing units - GPUs) can be used to speed up the performance of time consuming algorithms by means of massive parallelization. They are designed to execute many operations in parallel. odeint can utilize the power of GPUs by means of CUDA and Thrust, which is a STL-like interface for the native CUDA API.

Thrust also supports parallelization using OpenMP and Intel Threading Building Blocks (TBB). 
You can switch between CUDA, OpenMP and TBB parallelizations by a simple compiler switch. 
Hence, this also provides an easy way to get basic OpenMP parallelization into odeint. 
The examples discussed below are focused on GPU parallelization, though.

1
2
3
4
5

To use odeint with CUDA a few points have to be taken into account. First of all, the problem has to be well chosen. It makes absolutely no sense to try to parallelize the code for a three dimensional system, it is simply too small and not worth the effort. One single function call (kernel execution) on the GPU is slow but you can do the operation on a huge set of data with only one call. We have experienced that the vector size over which is parallelized should be of the order of 106 to make full use of the GPU. Secondly, you have to use Thrust’s algorithms and functors when implementing the rhs the ODE. This might be tricky since it involves some kind of functional programming knowledge.

Typical applications for CUDA and odeint are large systems, like lattices or discretizations of PDE, and parameter studies. We introduce now three examples which show how the power of GPUs can be used in combination with odeint.

The full power of CUDA is only available for really large systems where the number of coupled ordinary differential equations is of order N=106 or larger.
For smaller systems the CPU is usually much faster. 
You can also integrate an ensemble of different uncoupled ODEs in parallel as shown in the last example.

1
2
3
4

---

3 Phase oscillator ensemble 怎么使用GPU的大概流程

The first example is the phase oscillator ensemble from the previous section:

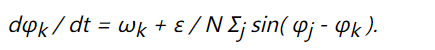
It has a phase transition at ε = 2 in the limit of infinite numbers of oscillators N. In the case of finite N this transition is smeared out but still clearly visible.

Thrust and CUDA are perfectly suited for such kinds of problems where one needs a large number of particles (oscillators). We start by defining the state type which is a thrust::device_vector. The content of this vector lives on the GPU. If you are not familiar with this we recommend reading the Getting started section on the Thrust website.

//change this to float if your device does not support double computation
typedef double value_type;

//change this to host_vector< ... > of you want to run on CPU
typedef thrust::device_vector< value_type > state_type;
// typedef thrust::host_vector< value_type > state_type;
1
2
3
4
5
6

Thrust follows a functional programming approach. If you want to perform a calculation on the GPU you usually have to call a global function like thrust::for_each, thrust::reduce, … with an appropriate local functor which performs the basic operation. An example is

struct add_two
{
    template< class T >
    __host__ __device__
    void operator()( T &t ) const
    {
        t += T( 2 );
    }
};

// ...

thrust::for_each( x.begin() , x.end() , add_two() );
1
2
3
4
5
6
7
8
9
10
11
12
13

This code generically adds two to every element in the container x.

For the purpose of integrating the phase oscillator ensemble we need

1. to calculate the system function, hence the r.h.s. of the ODE.
2. this involves computing the mean field of the oscillator example, i.e. the values of R and θ
   The mean field is calculated in a class mean_field_calculator

The mean field is calculated in a class mean_field_calculator

struct mean_field_calculator
{
    struct sin_functor : public thrust::unary_function< value_type , value_type >
    {
        __host__ __device__
        value_type operator()( value_type x) const
        {
            return sin( x );
        }
    };

    struct cos_functor : public thrust::unary_function< value_type , value_type >
    {
        __host__ __device__
        value_type operator()( value_type x) const
        {
            return cos( x );
        }
    };

    static std::pair< value_type , value_type > get_mean( const state_type &x )
    {
        value_type sin_sum = thrust::reduce(
                thrust::make_transform_iterator( x.begin() , sin_functor() ) ,
                thrust::make_transform_iterator( x.end() , sin_functor() ) );
        value_type cos_sum = thrust::reduce(
                thrust::make_transform_iterator( x.begin() , cos_functor() ) ,
                thrust::make_transform_iterator( x.end() , cos_functor() ) );

        cos_sum /= value_type( x.size() );
        sin_sum /= value_type( x.size() );

        value_type K = sqrt( cos_sum * cos_sum + sin_sum * sin_sum );
        value_type Theta = atan2( sin_sum , cos_sum );

        return std::make_pair( K , Theta );
    }
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

Inside this class two member structures sin_functor and cos_functor are defined. They compute the sine and the cosine of a value and they are used within a transform iterator to calculate the sum of sin(φ​k) and cos(φ​k). The classifiers host and device are CUDA specific and define a function or operator which can be executed on the GPU as well as on the CPU. The line

value_type sin_sum = thrust::reduce(
        thrust::make_transform_iterator( x.begin() , sin_functor() ) ,
        thrust::make_transform_iterator( x.end() , sin_functor() ) );
1
2
3

performs the calculation of this sine-sum on the GPU (or on the CPU, depending on your thrust configuration).

The system function is defined via

class phase_oscillator_ensemble
{

public:

    struct sys_functor
    {
        value_type m_K , m_Theta , m_epsilon;

        sys_functor( value_type K , value_type Theta , value_type epsilon )
        : m_K( K ) , m_Theta( Theta ) , m_epsilon( epsilon ) { }

        template< class Tuple >
        __host__ __device__
        void operator()( Tuple t )
        {
            thrust::get<2>(t) = thrust::get<1>(t) + m_epsilon * m_K * sin( m_Theta - thrust::get<0>(t) );
        }
    };

    // ...

    void operator() ( const state_type &x , state_type &dxdt , const value_type dt ) const
    {
        std::pair< value_type , value_type > mean_field = mean_field_calculator::get_mean( x );

        thrust::for_each(
                thrust::make_zip_iterator( thrust::make_tuple( x.begin() , m_omega.begin() , dxdt.begin() ) ),
                thrust::make_zip_iterator( thrust::make_tuple( x.end() , m_omega.end() , dxdt.end()) ) ,
                sys_functor( mean_field.first , mean_field.second , m_epsilon )
                );
    }

    // ...
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

Now, we are ready to put everything together. All we have to do for making odeint ready for using the GPU is to parametrize the stepper with the appropriate thrust algebra/operations:

typedef runge_kutta4< state_type , value_type , state_type , value_type , thrust_algebra , thrust_operations > stepper_type;

1
2

You can also use a controlled or dense output stepper, e.g.

typedef runge_kutta_dopri5< state_type , value_type , state_type , value_type , thrust_algebra , thrust_operations > stepper_type;
1

Then, it is straightforward to integrate the phase ensemble by creating an instance of the rhs class and using an integration function:

phase_oscillator_ensemble ensemble( N , 1.0 );
1

size_t steps1 = integrate_const( make_controlled( 1.0e-6 , 1.0e-6 , stepper_type() ) , boost::ref( ensemble ) , x , 0.0 , t_transients , dt );
1

We have to use boost::ref here in order to pass the rhs class as reference and not by value. This ensures that the natural frequencies of each oscillator are not copied when calling integrate_const. In the full example the performance and results of the Runge-Kutta-4 and the Dopri5 solver are compared.

The full example can be found at phase_oscillator_example.cu

---

其他文章已经代码：

1

https://archive.fosdem.org/2013/schedule/event/odes_cuda_opencl/attachments/slides/181/export/events/attachments/odes_cuda_opencl/slides/181/1430_Karsten.pdf

https://github.com/ddemidov/gpgpu_with_modern_cpp