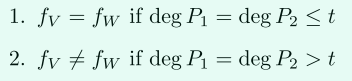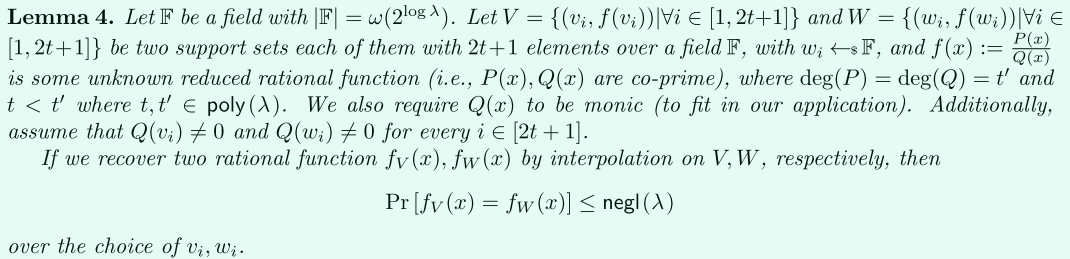本文记录阅读该论文的笔记。
本文基于阈值加法同态加密方案提出了一个新的允许方检查其输入集的交集是否大于的IPSI方案,该协议的通信复杂度为。
注意:指的是多少个参与方、是输入集的大小、是预先设定的阈值,也是阈值。
该方案基于The Communication Complexity of Threshold Private Set Intersection-2019:解读进行的改进。
该协议可以用于各方知道交集很大,但不知道具体多大时,可以使用!
摘要#

(1)该协议的通信复杂度不依赖于输入集的大小,而取决于阈值的大小
(2)基于阈值的PSI协议分为两部分:
- 交集的势测试(Cardinality Testing ),即测试参与方的交集是否大于
- PSI:计算交集
介绍#
两方阈值PSI:

(1)双方先检测交集大小是否
(2)若满足,则求交(获取交集);否则,什么也得不到(获取不到交集)
标准PSI和阈值PSI的对比:
- 标准的PSI更在乎交集,而不在乎交集的大小,而阈值PSI更关注交集的大小。
- 阈值PSI的通信量较少,只取决于阈值的大小;标准的PSI通信量取决于输入集合的大小。
阈值PSI现状:
只有以下方案进行了讨论:
(1)【Privatepool: Privacy-preserving ridesharing-2017】
(2)【An algebraic approach to maliciously secure private set intersection-2019】
(3)【The communication complexity of threshold private set intersection-2019】
其中只有(3)的通信复杂度不依赖于,方案是两方场景。
(4)【Multi-party threshold private set intersection with sublinear communication-2021】
这也是一个多方阈值PSI,使用FHE,通信复杂度为,也提出了一个TPKE加密方案实现了:只有当各方的交集足够大时,各方才能求交集。还可以秘密的计算汉克尔矩阵的行列式(矩阵大小的线性时间内)。
阈值PSI的应用:
(1)约会APP
(2)生物特征认证
(3)拼车【Privatepool: Privacy-preserving ridesharing 】
假设两个(或更多)方正在使用拼车应用程序,如果他们的路线有很大的交集,它允许他们共享车辆。然而由于隐私问题,他们不想公开他们的行程。阈值PSI可以解决该问题,各方可以联合执行一个阈值PSI协议,了解路线的交叉点,如果交叉点足够大,共享一辆车,否则,他们就不共享一辆车,也能保证用户的路线隐私。
阈值PSI#
当前的阈值PSI主要分为两步:
(1)Cardinality Testing:就是各方检测交集是否大于
(2)PSI:如果满足(1),则输出交集;否则没有输出
合适的阈值一定是2的次幂 ,如果交集大于,则Cardinality Testing对于阈值就成功,因为,所以协议的通信复杂度只取决于阈值的大小。
解释有点牵强,或许我没理解
是什么?
贡献#
(1)多方Cardinality Testing
- 较上面的Cardinality Testing,这里给出了满足多方的Cardinality Testing
- 通信复杂度为
- 并给出一些新的线性计算(linear algebra):求密文矩阵相乘、求密文矩阵的秩、求密文矩阵的逆等
该协议在【Secure linear algebra using linearly recurrent sequences-2007】【Communication efficient secure linear algebra-2006】的(两方)基础上构建的多方阈值PSI。
(2)多方阈值PSI
这里也是将一个两方的协议改为多方。
回顾一下两方的情况:
两方Alice和Bob各有数据和,其大小都是,阈值,如果,则求出交集。
我们方案基于【The communication complexity of threshold private set intersection-2019】论文,这是一个两方的阈值PSI协议:

(1)若交集大于
(2)计算交集
两方将数据编码到多项式中,得到和在一个大的有限域上,其中,然后只要满足,则:
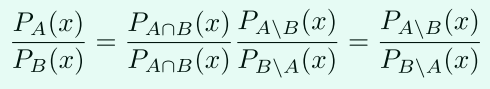
且,所以两方只需要在上计算个点。然后将这些点插值得到,然后求出分母,继而求出交集多项式
紧接上文问题:具体如何根据,然后求出分母?
Bob不能恢复出分子,否则方案就不安全了,所以这里使用Oblivious Linear Evaluation (OLE)技术用于“掩盖”分子项(随机化)。
该协议只有满足,才是安全的,否则就会泄露额外的信息,所以双方应该先执行Cardinality Testing操作,来保证协议是满足的。
扩展到多方的限制:
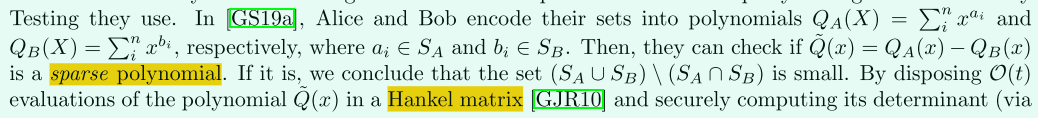
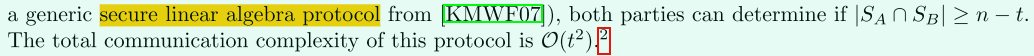
这里讲的是Cardinality Testing如何扩展为多方:
参与方先将数据编码到多项式中,得到和,其中,检测是否是一个稀疏多项式(sparse polynomial),若是,则判断集合是小集合(small),通信复杂度为。
那问题来了:
(1)如何判断多项式是否时稀疏的?
(2)如何判断集合是小的?
如果将其扩展为多方,对于个参与者,有:,如果很小的话,那该多项式就是稀疏的,那我们要是能计算该多项式的稀疏性,那么Cardinality Testing协议的总通信量变为。
主要方法#
1、安全线性代数(Secure Linear Algebra )
来源【Secure linear algebra using linearly recurrent sequences 】
有两个参与方,一方有矩阵的加密,另一方有对应的解密私钥,他们想要对这个密文矩阵做运算(线性计算,linear algebra related ),比如:求逆矩阵的行列式、秩或者计算出,对于,给出加密的。
我们可以将该问题扩展到方,对于N个参与者,每人有一份私钥的分享值,此外有一个加密的矩阵,目的是要对这个加密的矩阵做运算(线性计算,linear algebra related)。
我们发现可以将【secure linear algebra】协议扩展为多方场景,通过使用具有加法同态性的阈值PKE代替具有加法同态的PKE和GC代替来实现,所以该方案允许N方在阈值PKE下解决这个线性代数问题。
2、多方势检测(Cardinality Testing via Degree Test of a Rational Function )
对于参与方编码的多项式,有:
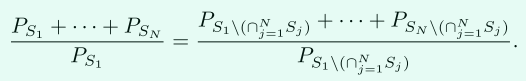
若交集大小大于,则。
以上是求交的方法!
所以Cardinality Testing有以下问题:
对于有理函数,能否安全的判断,进而通过插值个点得到?
另外,插值有理函数可以看作是求解线性方程组,所以通过前面介绍的“Secure Linear Algebra”,可以安全(不泄露额外信息)的计算“degree test”,换句话说,这能判断交集大小是否小于,同时不泄露额外信息。
3、多方计算交集
这里的方法可以看作是【The communication complexity of threshold private set intersection 】的推广。
各方将其数据进行编码为多项式,并且知道交集大小,各方联合计算出有理函数,然后插值个点值,方恢复出分母,求出交集。
该方案和【The communication complexity of threshold private set intersection】的不同之处就是,将“OLE calls”换成了基于阈值的PKE(具有加法同态性),可以看成多方OLE的替换。
4、安全性
在UC框架下证明了Cardinality Testing的安全,但还存在一个问题,就是“secure linear algebra”协议不能证明是UC安全的,因为输入是在公钥加密的密文,在UC设置中,输入是来自其他地方。
使用Externalized UC框架解决该问题,在该框架下,安全的“linear algebra ideal functionalities”共享公钥,每人一个私钥的分享份,使用这种方法证明协议的安全性。
由于“secure linear algebra”协议是安全的,如果它们都共享相同的公钥,那么在“Cardinality Testing”中,我们只需要创建此公钥并共享,所以我们可以证明“Cardinality Testing”是UC安全的。
其他的证明方式:仅证明住主协议的安全性,而不单独证明每个字协议的安全性。
推荐参考:UC安全,接下来需要看Externalized UC!
基础#
是一个有限集合,表示从中随机采样,表示的势(cardinality);个参与者;给出两个不可区分的分布;安全参数
阈值的PKE#
UC框架和理想函数#
方案使用UC框架【A new paradigm for cryptographic protocols】分析安全性,在该协议中,只考虑半诚实敌手。

其中:
- 是环境
- 是协议
- 是真实世界
- 是理想函数
- 是模拟器
理想情况下的基于阈值的多方PSI:
只有当交集够大时,各方才会求交集。
Externalized UC of Global Setup:
externalized UC emulation (EUC)来源于【Universally composable security with global setup】,这是全局设置(global setup)的UC框架(简单版)

多项式插值#
下面介绍使用一个随机多项式去“混淆/遮盖”一个级数小于t的多项式:
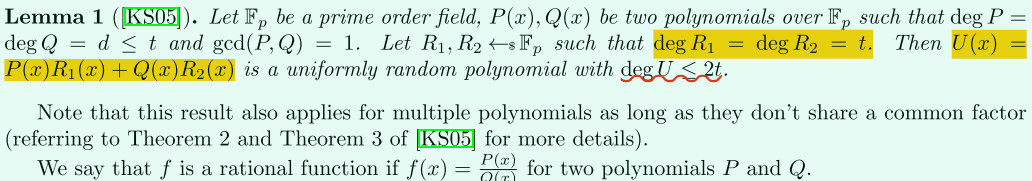
这种方式也可以用于多个多项式(多方),只要他们不共享一个因子(common factor)。
什么意思,不能约么?
下面介绍如何通过插值恢复出这个有理函数以及证明该函数是唯一的

其中的级数为,的级数为,则可一通过插值个点唯一的插值出,若是首一的(monic),则只需要个点。
给定集合,大小为,可以根据这个点唯一的插值出。
引理#
Oblivious Degree Test for Rational Functions#
下面给出一个多方协议下求线性计算,通信复杂度为。
多方求线性函数(Oblivious Linear Algebra)#
多方求加密矩阵乘#
具体实现如下:
(1)初始化:各方,共享公钥,以及每方各有一份私钥分享份
(2)输入:输入两个矩阵的加密,其中
(3)输出:各方得到

其思想就是:
但存在一个问题:(以三方为例)
最后得到的,因为在上面框红处,没有自乘!
多方求加密矩阵的秩#
不太懂
多方求线性函数#
思想是将问题约减为最小多项式。
是一个非奇异矩阵(non-singular matrix),也叫做满秩矩阵。
都是密文形式。
功能:

多方势检测(Oblivious Degree Test)#
功能:判断多方的交集数量是否大于阈值,若满足,则输出1,否则输出0。

主要思想是:
在两个不同数据集上插值出有理函数,并检查两次实验的结果是否相同。
插值有理函数可以看作求解线性函数,因此可以使用“secure linear algebra”求解线性函数。
最后各方只需要安全的检查是否成立!
给定有理函数,其中有相同的级数,并给定两个集合,下面的协议是判断这个有理数函数的级数是否小于阈值:

下面具体来分析一波:
(1)初始化
- 各方共享公钥,且每人有一个私钥份;
- 假设各方可以正常执行理想函数:;
- 各方共享一组随机数;
(2)参与方输入
输入:,其中,是两个级数为的多项式
(3)设置
将的输入拆分为两部分和。
所以得到了对点值和。
由上面的点值构造两个密态线性系统:
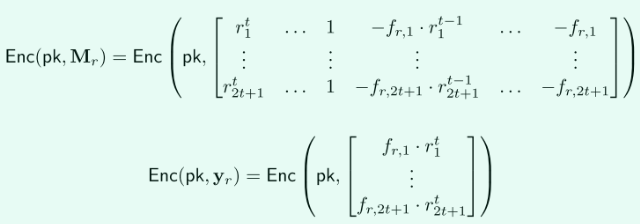
其中,是一个维数为的方阵,是一个长度为的向量。
这样就得到了加密的和。
(4)各方联合计算
计算:,如果结果不为0,则停止协议,其中使用了两次和。
即参与方联合测试和解密后是否为0,若为0,则继续。
(5)各方联合计算
利用计算上面的两个线性函数,每方得到和,其中;和各是长度为和的向量。
这时各方能根据由得到密态的,得到密态的。
(6)各方联合计算
计算出:,和,
(7)判断
各方使用检查是否等于0(即对解密)。如果是,输出0;如果不是,输出1。
优化#
我们考虑在对插值生成,当时,我们就不能求了。

解决办法就是,去掉该点:
使得
具体来讲,就是计算出点值对,。
这里的指的是
然后再分别构造出,后面的不变。
另外协议也能推广到的情况。
多方阈值PSI#
该协议的重点就是cardinality test protocol,能够安全的判断N方数据的交集和阈值的大小关系。
安全的势检测(Secure Cardinality Testing)#
1、理想功能

2、具体实现

总结一下:
(1)各方先各自将数据编码为多项式,然后求出个点值,加密这些点,得到个密态值,广播出去。
(2)得到个,计算得到,形成密态点值对,并和私钥一起发送给理想函数。
(3)其他参与方也将各自的私钥发送给理想函数,从而判断分子和分母的级数是否最大为,然后输出结果。
完整的多方阈值PSI协议#
在该协议中,通过使用TPKE扩展了之前的方案,具体协议如下:

总结一下:
(1)各方先将数据发送给理想函数,检测交集大小和阈值的大小关系。
(2)再通过理想函数生成密钥:各方共享公钥,各自有一个私钥份。
(3)各方执行:
- 将数据编码为多项式,计算出个点值。
- 采样,使得。
- 加密:,然后广播出去。
(4)将收到的对应的密文相加得到个值,再将其广播出去。
(5)联合解密出。
(6)计算点,得到点值对,将其插值出函数,再恢复出分母。
(7)根据自己数据计算出,根据,判断是否在交集中。
(8)广播交集。
在这里给出了详细如何根据,计算出交集!
这样就能根据个点插值出,再“恢复”出分母,进而带入数据元素判断是否为交集元素。
总结#
1、关键点“cardinality test protocol”,也是最难理解的
2、如何根据恢复出分母?