-
LeetCode 1175. 质数排列(质数判断+组合数学)
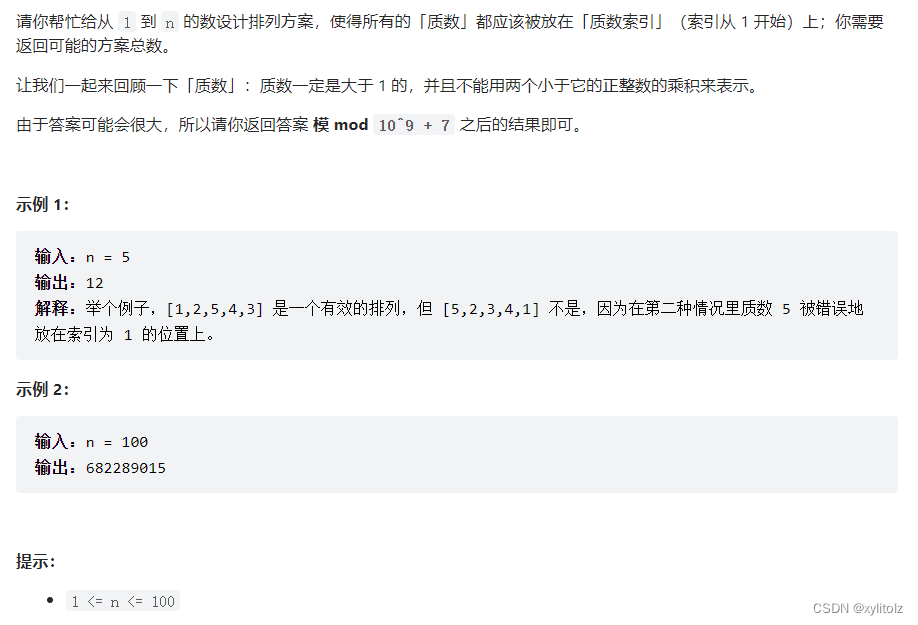
0 题目
1 解题思路
1.1 质数判断+组合数学
本 题 总 的 方 案 数 = 「 所 有 质 数 都 放 在 质 数 索 引 上 的 方 案 数 」 × 「 所 有 合 数 都 放 在 合 数 索 引 上 的 方 案 数 」 本题总的方案数=「所有质数都放在质数索引上的方案数」\times \\ 「所有合数都放在合数索引上的方案数」 本题总的方案数=「所有质数都放在质数索引上的方案数」×「所有合数都放在合数索引上的方案数」
「所有质数都放在质数索引上的方案数」:
- 首先求出
[
1
,
n
]
[1,n]
[1,n]范围内所有质数的个数
p
r
i
m
e
N
u
m
primeNum
primeNum
- 枚举100以内所有质数+二分
- 试除法
- 再求出质数个数 primeNum \textit{primeNum} primeNum 的阶乘即为方案数
「所有合数都放在合数索引上的方案数」:
- n − p r i m e N u m n - primeNum n−primeNum即为所有合数的个数,再求其阶乘即为方案数
排列:
A ( m , n ) = n ! ( n − m ) ! A(m, n) = \frac{n!}{(n - m)!} A(m,n)=(n−m)!n!组合:
C ( m , n ) = n ! m ! × ( n − m ) ! C(m, n) = \frac{n!}{m! \times (n - m)!} C(m,n)=m!×(n−m)!n!1.1.1 代码实现
1.1.1.1 枚举100以内所有质数+二分
class Solution { // 枚举100以内所有质数 private static int[] PRIME = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97}; private static final int MOD = 1000000007; public int numPrimeArrangements(int n) { // 利用二分求取质数个数 int primeNum = binarySearch(n) + 1; // 利用阶乘求方案数 return (int) (calcFactorial(primeNum) * calcFactorial(n - primeNum) % MOD) ; } private long calcFactorial(int m) { long res = 1; while (m != 0) { res *= m; res %= MOD; m--; } return res; } private int binarySearch(int n) { int left = 0, right = PRIME.length - 1; while (left < right) { int mid = left + (right - left + 1) / 2; if (PRIME[mid] > n) { right = mid - 1; } else { left = mid; } } return left; } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
1.1.1.2 试除法
class Solution { private static final int MOD = 1000000007; public int numPrimeArrangements(int n) { // 试除法求取质数个数 int primeNum = 0; for (int i = 1; i <= n; i++) { if (isPrime(i)) { primeNum++; } } // 利用阶乘求方案数 return (int) (calcFactorial(primeNum) * calcFactorial(n - primeNum) % MOD); } public boolean isPrime(int n) { if (n == 1) { return false; } for (int i = 2; i * i <= n; i++) { if (n % i == 0) { return false; } } return true; } public long calcFactorial(int n) { long res = 1; for (int i = 1; i <= n; i++) { res *= i; res %= MOD; } return res; } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
2 Reference
- 首先求出
[
1
,
n
]
[1,n]
[1,n]范围内所有质数的个数
p
r
i
m
e
N
u
m
primeNum
primeNum
-
相关阅读:
计算机毕设(附源码)JAVA-SSM基于云数据库的便民民宿租赁系统
普通用户如何利用小红书赚钱呢?小红书的流量是真的吗?
三大运营商乘风破浪,为什么离不开BAT等互联网企业?
nlp中的对抗训练比较
【建造者设计模式详解】Java/JS/Go/Python/TS不同语言实现
51.Python-web框架-Django开始第一个应用的增删改查
MySQL -- DQL
ITem2 + Oh My Zsh配置
关于React
UNIAPP实战项目笔记29 购物车设置自定义导航栏
- 原文地址:https://blog.csdn.net/xylitolz/article/details/125534212
