高斯消元法

题目描述

这次，alice梦回大一上的线代课堂。她梦到线代老师在考试中出了这道压轴题：

（12分）已知一个n阶方阵，以及一个列向量A，要求编程求解：

(1)满足的列向量x（如果不存在唯一解，输出"No Solution!"）.（3分）

 

(2)矩阵的行列式det(A).（5分）

(3)矩阵的秩r(A),以及的零空间的维度dim(N(A)).（4分）

对于第(1)问，alice很清楚这就是高斯消元，因此她很快就在网上查到了解决这个问题的伪代码：

 const double eps = 1e-8;
 int guass_elimination(double A[maxn][maxn], int n) // 高斯消元
 {
     int i, j, k, r;
     for(i = 0; i < n; i++) { // 消元
         r = i;
         for(j = i + 1; j < n; j++) if(fabs(A[j][i]) > fabs(A[r][i])) r = j;
         if(fabs(A[r][i]) < eps) return 0;  // 无解
         if(r != i) for(j = 0; j <= n; j++) swap(A[i][j], A[r][j]);
         for(k = i + 1; k < n; k++) {
             double f = A[k][i] / A[i][i];
             for(j = i; j <= n; j++) A[k][j] -= f * A[i][j];
         }
     }
     for(i = n - 1; i >= 0; i--) {  // 回代
         for(j = i + 1; j < n; j++) {
             A[i][n] -= A[j][n] * A[i][j];
         }
         A[i][n] /= A[i][i];
     }
     return 1; 
 }

其中，fabs(a)表示浮点数a的绝对值，swap(a,b)的作用是交换两个数a,b。函数传递的两个参数分别是增广矩阵(A|b)以及行数。这个增广矩阵在函数作用之后，假设只存在唯一解，则矩阵的第(n+1)列就是符合题意的列向量x。

然而对于第(2)(3)问，则是一筹莫展。

眼看就要交卷了，这时rawslee通过心灵感应给了她指点：

"密切关注题目的第一问。"

在这个提示下，alice重新审视了上面的伪代码，只进行了一些微小的调整以及增加一些语句，便马上写出了第(2)(3)问，愉快的在梦中取得了满分。你知道她是怎么做出来的吗？

输入格式

第一行一个正整数T，表示数据组数。

对于每组数据：

第一行一个正整数n，表示矩阵A的大小为n行n列。

之后n行每行n个实数（最多有2位小数），表示矩阵A，第i行第j列表示矩阵的元素Aij。

输出格式

对于每组数据，输出三个数，分别代表det(A),（保留2位小数）,r(A),dim(N(A)).

每组输出以换行符结尾。

数据范围

.

 

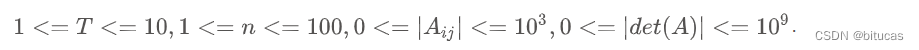
样例输入1

1 3 1 3 4 1 4 7 9 3 2

样例输出1

38.00 3 0

样例输入2

1

3

1.50 3.50 4.50

1.50 3.50 4.50

9.20 3.20 2.20

样例输出2

0.00 2 1

友情提醒

为保持精度，建议使用double类型进行计算。

# include<stdio.h>
# include<math.h>
# include<stdlib.h>
/*
（12分）已知一个阶方阵，以及一个列向量，要求编程求解：
(1)满足的列向量（如果不存在唯一解，输出"No Solution!"）.（3分）
(2)矩阵的行列式.（5分）
(3)矩阵的秩,以及的零空间的维度.（4分）
对于第(1)问，很清楚这就是高斯消元，因此她很快就在网上查到了解决这个问题的伪代码：
 const double eps = 1e-8;
 int guass_elimination(double A[maxn][maxn], int n) // 高斯消元
 {
     int i, j, k, r;
     for(i = 0; i < n; i++) { // 消元
         r = i;
         for(j = i + 1; j < n; j++) if(fabs(A[j][i]) > fabs(A[r][i])) r = j;
         if(fabs(A[r][i]) < eps) return 0;  // 无解
         if(r != i) for(j = 0; j <= n; j++) swap(A[i][j], A[r][j]);
         for(k = i + 1; k < n; k++) {
             double f = A[k][i] / A[i][i];
             for(j = i; j <= n; j++) A[k][j] -= f * A[i][j];
         }
     }
     for(i = n - 1; i >= 0; i--) {  // 回代,求方程右边的向量 
         for(j = i + 1; j < n; j++) {
             A[i][n] -= A[j][n] * A[i][j];
         }
         A[i][n] /= A[i][i];
     }
     return 1; 
 }
其中，fabs(a)表示浮点数a的绝对值，swap(a,b)的作用是交换两个数a,b。
函数传递的两个参数分别是增广矩阵以及行数。这个增广矩阵在函数作用之后，
假设只存在唯一解，则矩阵的第列就是符合题意的列向量。
然而对于第(2)(3)问，则是一筹莫展。
眼看就要交卷了，这时通过心灵感应给了她指点：
"密切关注题目的第一问。"
在这个提示下，重新审视了上面的伪代码，
只进行了一些微小的调整以及增加一些语句，便马上写出了第(2)(3)问
输入格式
第一行一个正整数，表示数据组数。
对于每组数据：
第一行一个正整数，表示矩阵的大小为行列。
之后行每行个实数（最多有2位小数），表示矩阵，第行第列表示矩阵的元素。
输出格式
对于每组数据，输出三个数，分别代表（保留2位小数）,,.
每组输出以换行符结尾。
样例输入1
1 3 1 3 4 1 4 7 9 3 2
样例输出1
38.00 3 
样例输入2
1
3
1.50 3.50 4.50
1.50 3.50 4.50
9.20 3.20 2.20
样例输出2
0.00 2 1
友情提醒
为保持精度，建议使用double类型进行计算。
*/
int guass_elimination(double *A,int n, double * det, int *dim) // 高斯消元
{//提示中的代码是对增广矩阵操作，而这里只要对方阵操作就行，所以
//循环上限有所修改，对增广部分的代码也删了 
    int i, j, k, r, flag = 1, time = 0;//time交换行的次数 
    double temp;						//交换行，行列式取相反数 
    for(i = 0; i < n; i++) 
	{ // 消元
    	r = i;
    	for(j = i + 1; j < n; j++)//按列从左向右遍历 
			if(fabs(A[j*n+i]) > fabs(A[r*n+i]))//第i列中从对角线往下找最大的那个 
				r = j;						//其所在行为r 
   		if(fabs(A[r*n+i]) < 1e-8) //若最大的都是0 
		   flag = 0;  // 无数解，降秩 
    	if(r != i) 
		{
			for(j = 0; j < n; j++)
			{ //将第r行与第i行交换 
				temp = A[i*n+j];
				A[i*n+j] = A[r*n+j];
				A[r*n+j] = temp;
			}
			time ++;
		}
		
    	for(k = i + 1; k < n; k++) //将第i行以下的减f倍第i行（把最左边的 
		{							//即第i列）全消为0 
			if(fabs(A[i*n+i]) > 1e-8)
			{
				double f = A[k*n+i] / A[i*n+i];//f存第i列要减的倍数 
        		for(j = i; j < n; j++)
					A[k*n+j] -= f * A[i*n+j];
			}
        	
   	 	}
    }//从而化为阶梯型 (注意是方阵 
    *det = pow(-1, time);
    
    if(flag == 1)
    {
    	for(int m = 0; m < n; m ++)
    	{
    		*det *= A[m*n+m];
		}
	}
	else
	{
		for(int m = 0; m < n; m ++)
    	{
    		if(fabs(A[m*n+m]) > 1e-8)
    		{
    			*dim = *dim + 1;//在对角线上数维数 
			}
		}
	}
    
    return flag; 
 }
int main()
{
	int num;
	scanf("%d", &num);//数据组数 
	int flag[num], dim[num], n[num];//flag是否满秩，dim为秩，n为总维数 
	double det[num];//行列式 
	for(int i = 0; i<num;i++)
	{
		det[i] = 1;
		dim[i]=0;
	}
	
	for(int q = 0; q < num; q ++)
	{
		scanf("%d", &n[q]);
		double *a= (double*) malloc (n[q]*n[q] * sizeof(double));
		//用malloc而不用可变二维数组
		//因为可变二维数组传入函数需要在函数原型中确定列数，但列数非
		//常数，又函数原型在主函数获得列数前（此时列数未定义）
		//故此时无法用二维数组的模式定位，不如用一维 
		for(int p = 0; p < n[q]*n[q]; p ++)
		{
			scanf("%lf", (a + p));//a为地址 
		}
		flag[q] = guass_elimination(a, n[q], &det[q], &dim[q]);
		//函数出口最多一个返回值 
	}
	
	for(int q = 0;q < num; q ++)
	{
		if(flag[q] != 0)//满秩 
		{
			printf("%.2lf %d %d\n", det[q], n[q], 0);
		}
		else
		{
			printf("0.00 %d %d\n", dim[q], n[q] - dim[q]);
		}
	}
	
	return 0;
}