• AVL 平衡二叉搜索树

    二叉搜索树（BST）虽能缩短查找效率，但如果数据有序或接近有序，BST将退化为单支树，此时查找元素就相当于在顺序表中搜索元素，效率低下。

    那么此时如果能保证每个结点的左右子树高度差的绝对值不超过1，就可以降低树的高度，从而减少平均搜索长度。所以AVL带着这个使命诞生了。

    一、AVL 

    在二叉树中，如果每个结点的子树的高度差距为0、1或-1，则称这棵树是平衡二叉树，即AVL。

    二、平衡二叉树

    执行插入或删除操作后如果导致了AVL的不平衡，那么我们需要执行旋转操作来重新平衡这棵树。旋转操作主要有LL、RR、LR、RL四种类型。

    1、LL

    向左子树中的左孩子插入新结点后导致不平衡，此时需要右旋操作：

    旋转后平衡二叉树将B看作新root， 将E结点与A.left相连，再将A与B.right相连，最后得到新的AVL。

    1.     private void balanceLL(AVLTreeNode<E> A, TreeNode<E> parentOfA){
    2.         TreeNode<E> B = A.left;
    3.         if(A == root){
    4.             root = B;
    5.         }else{
    6.             if(parentOfA.left == A){
    7.                 parentOfA.left = B;
    8.             }else{
    9.                 parentOfA.right = B;
    10.             }
    11.         }
    12.  
    13.         A.left = B.right;
    14.         B.right = A;
    15.         updateHeight((AVLTreeNode<E>) A);

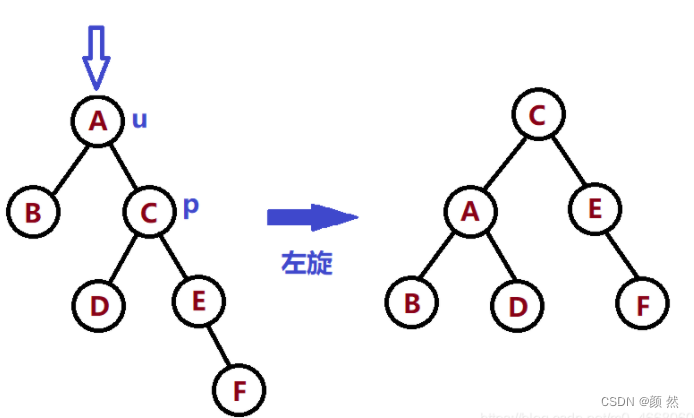
    2、RR

    和LL相反，向右子树中的右孩子插入新结点后导致的不平衡，此时需要左旋操作： 

    1.     private void balanceRR(TreeNode<E> A, TreeNode<E> parentOfA){
    2.         TreeNode<E> B =A.right;
    3.  
    4.         if(A == root){
    5.             root  = B;
    6.         }else{
    7.             if(parentOfA.left == A){
    8.                 parentOfA.left = B;
    9.             }else{
    10.                 parentOfA.right = B;
    11.             }
    12.         }
    13.  
    14.         A.right = B.left;
    15.         B.left = A;
    16.         updateHeight((AVLTreeNode<E>)A);
    17.         updateHeight((AVLTreeNode<E>)B);
    18.     }

    3、LR 

    左儿子左旋，根结点右旋：

    1.     private void balanceLR(TreeNode<E> A, TreeNode<E> parentOfA){
    2.         TreeNode<E> B = A.left;
    3.         TreeNode C = B.right;
    4.  
    5.         if(A == root){
    6.             root = C;
    7.         }else{
    8.             if(parentOfA.left == A){
    9.                 parentOfA.left = C;
    10.             }else {
    11.                 parentOfA.right = C;
    12.             }
    13.         }
    14.  
    15.         A.left = C.right;
    16.         B.right = C.left;
    17.         C.left = B;
    18.         C.right = A;
    19.  
    20.         updateHeight((AVLTreeNode<E>)A);
    21.         updateHeight((AVLTreeNode<E>)B);
    22.         updateHeight((AVLTreeNode<E>)C);
    23.     }

    4、RL

    右儿子右旋，根结点左旋：

    1.     private void balanceRL(TreeNode<E> A, TreeNode<E> parentOfA){
    2.         TreeNode<E> B = A.right;
    3.         TreeNode<E> C = B.left;
    4.  
    5.         if(A == root){
    6.             root = C;
    7.         }else{
    8.             if(parentOfA.left == A){
    9.                 parentOfA.left = C;
    10.             }else{
    11.                 parentOfA.right = C;
    12.             }
    13.         }
    14.         A.right = C.left;
    15.         B.left = C.right;
    16.         C.left = A;
    17.         C.right = B;
    18.  
    19.         updateHeight((AVLTreeNode<E>)A);
    20.         updateHeight((AVLTreeNode<E>)B);
    21.         updateHeight((AVLTreeNode<E>)C);
    22.     }

     三、Java实现AVLTree类

    AVLTree类继承BST类。

    1. public class AVLTree<E extends Comparable<E>> extends BST<E>{
    2.     public AVLTree() {
    3.     }
    4.  
    5.     public AVLTree(E[] objects) {
    6.         super(objects);
    7.     }
    8.  
    9.     // 插入方法和BST中的方法一样，只不过每次添加后需要检查平衡
    10.     @Override
    11.     public boolean insert(E e){
    12.         boolean success = super.insert(e);
    13.         if(!success){
    14.             return false;
    15.         }else{
    16.             balancePath(e);  // 检查是否需要平衡操作
    17.         }
    18.         return true;
    19.     }
    20.  
    21.     private void updateHeight(AVLTreeNode<E> node){
    22.         if(node.left == null && node.right == null){
    23.             node.height = 0;
    24.         }else if(node.left == null){
    25.             node.height = 1 + ((AVLTreeNode<E>)(node.right)).height;
    26.         }else if(node.right == null){
    27.             node.height = 1 + ((AVLTreeNode<E>)(node.left)).height;
    28.         }else
    29.             node.height = 1 + Math.max(((AVLTreeNode<E>)(node.right)).height,((AVLTreeNode<E>)(node.left)).height);
    30.     }
    31.  
    32.     // 平衡一条路径上的结点
    33.     private void balancePath(E e){
    34.         java.util.ArrayList<TreeNode<E>> path = path(e);  // 获取包含e的结点到根结点的路径
    35.         for(int i = path.size() - 1; i >= 0; i--){
    36.             AVLTreeNode<E> A = (AVLTreeNode<E>)(path.get(i));
    37.             updateHeight(A);  // 更新高度
    38.             AVLTreeNode<E> parentOfA = (A == root) ? null : (AVLTreeNode<E>)(path.get(i - 1));
    39.  
    40.             switch(balanceFactor(A)){  // 检查平衡因子，检查是否需要旋转
    41.                 case -2 :
    42.                     if(balanceFactor((AVLTreeNode<E>)A.left) <= 0){
    43.                         balanceLL(A,parentOfA);
    44.                     }else{
    45.                         balanceLR(A,parentOfA);
    46.                     }
    47.                     break;
    48.                 case +2 :
    49.                     if(balanceFactor((AVLTreeNode<E>)A.right) >= 0){
    50.                         balanceRR(A, parentOfA);
    51.                     }else{
    52.                         balanceRL(A, parentOfA);
    53.                     }
    54.             }
    55.         }
    56.     }
    57.  
    58.     private int balanceFactor(AVLTreeNode<E> node){
    59.         if(node.left == null){
    60.             return -node.height;
    61.         }else if(node.left == null){
    62.             return +node.height;
    63.         }else
    64.             return ((AVLTreeNode<E>)node.right).height - ((AVLTreeNode<E>)node.left).height;
    65.     }
    66.  
    67.     private void balanceLL(AVLTreeNode<E> A, TreeNode<E> parentOfA){
    68.         TreeNode<E> B = A.left;
    69.         if(A == root){
    70.             root = B;
    71.         }else{
    72.             if(parentOfA.left == A){
    73.                 parentOfA.left = B;
    74.             }else{
    75.                 parentOfA.right = B;
    76.             }
    77.         }
    78.  
    79.         A.left = B.right;
    80.         B.right = A;
    81.         updateHeight((AVLTreeNode<E>) A);
    82.         updateHeight((AVLTreeNode<E>) B);
    83.     }
    84.  
    85.     private void balanceLR(TreeNode<E> A, TreeNode<E> parentOfA){
    86.         TreeNode<E> B = A.left;
    87.         TreeNode C = B.right;
    88.  
    89.         if(A == root){
    90.             root = C;
    91.         }else{
    92.             if(parentOfA.left == A){
    93.                 parentOfA.left = C;
    94.             }else {
    95.                 parentOfA.right = C;
    96.             }
    97.         }
    98.  
    99.         A.left = C.right;
    100.         B.right = C.left;
    101.         C.left = B;
    102.         C.right = A;
    103.  
    104.         updateHeight((AVLTreeNode<E>)A);
    105.         updateHeight((AVLTreeNode<E>)B);
    106.         updateHeight((AVLTreeNode<E>)C);
    107.     }
    108.  
    109.     private void balanceRR(TreeNode<E> A, TreeNode<E> parentOfA){
    110.         TreeNode<E> B =A.right;
    111.  
    112.         if(A == root){
    113.             root  = B;
    114.         }else{
    115.             if(parentOfA.left == A){
    116.                 parentOfA.left = B;
    117.             }else{
    118.                 parentOfA.right = B;
    119.             }
    120.         }
    121.  
    122.         A.right = B.left;
    123.         B.left = A;
    124.         updateHeight((AVLTreeNode<E>)A);
    125.         updateHeight((AVLTreeNode<E>)B);
    126.     }
    127.  
    128.     private void balanceRL(TreeNode<E> A, TreeNode<E> parentOfA){
    129.         TreeNode<E> B = A.right;
    130.         TreeNode<E> C = B.left;
    131.  
    132.         if(A == root){
    133.             root = C;
    134.         }else{
    135.             if(parentOfA.left == A){
    136.                 parentOfA.left = C;
    137.             }else{
    138.                 parentOfA.right = C;
    139.             }
    140.         }
    141.         A.right = C.left;
    142.         B.left = C.right;
    143.         C.left = A;
    144.         C.right = B;
    145.  
    146.         updateHeight((AVLTreeNode<E>)A);
    147.         updateHeight((AVLTreeNode<E>)B);
    148.         updateHeight((AVLTreeNode<E>)C);
    149.     }
    150.  
    151.     // 和BST中的删除方法一样，只不过需要判断下是否平衡
    152.     @Override
    153.     public boolean delete(E element){
    154.         if (root == null) {
    155.             return false;
    156.         }
    157.         TreeNode<E> parent = null;
    158.         TreeNode<E> current = root;
    159.         while(current != null){
    160.             if(element.compareTo(current.element) < 0){
    161.                 parent = current;
    162.                 current = current.left;
    163.             }else if(element.compareTo(current.element) > 0){
    164.                 parent = current;
    165.                 current = current.right;
    166.             }else break;
    167.         }
    168.         if(current == null){
    169.             return false;
    170.         }
    171.  
    172.         if(current.left == null){
    173.             if(parent == null){
    174.                 root = current.right;
    175.             }else {
    176.                 if(element.compareTo(parent.element) < 0){
    177.                     parent.left = current.right;
    178.                 }else{
    179.                     parent.right = current.right;
    180.                 }
    181.                 balancePath(parent.element);
    182.             }
    183.         }else{
    184.             TreeNode<E> parentOfRightMost = current;
    185.             TreeNode<E> rightMost = current.left;
    186.  
    187.             while(rightMost.right != null){
    188.                 parentOfRightMost = rightMost;
    189.                 rightMost = rightMost.right;
    190.             }
    191.             current.element = rightMost.element;
    192.  
    193.             if(parentOfRightMost.right == rightMost){
    194.                 parentOfRightMost.right = rightMost.left;
    195.             }else{
    196.                 parentOfRightMost.left = rightMost.left;
    197.             }
    198.             balancePath(parentOfRightMost.element);
    199.         }
    200.         size--;
    201.         return true;
    202.     }
    203.  
    204.     protected static class AVLTreeNode<E> extends BST.TreeNode<E>{
    205.         protected int height = 0;
    206.  
    207.         public AVLTreeNode(E e){
    208.             super(e);
    209.         }
    210.     }
    211. }

    四、测试AVLTree类

    1. public class TestAVLTree {
    2.     public static void main(String[] args){
    3.         AVLTree<Integer> tree = new AVLTree<Integer>(new Integer[]{25, 20 ,5});
    4.         System.out.print("After inserting 25,20,,5: ");
    5.         printTree(tree);
    6.  
    7.         tree.insert(34);
    8.         tree.insert(50);
    9.         System.out.print("\nAfter inserting 34, 50 : ");
    10.         printTree(tree);
    11.  
    12.         tree.insert(30);
    13.         System.out.print("\nAfter inserting 30 : ");
    14.         printTree(tree);
    15.  
    16.         tree.insert(10);
    17.         System.out.print("\nAfter inserting 10 : ");
    18.         printTree(tree);
    19.  
    20.         tree.delete(34);
    21.         tree.delete(30);
    22.         tree.delete(50);
    23.         System.out.print("\nAfter removing 34, 30, 50: ");
    24.         printTree(tree);
    25.  
    26.         tree.delete(5);
    27.         System.out.print("\nAfter removing 5 : ");
    28.         printTree(tree);
    29.  
    30.         System.out.print("\nTraverse the element in the tree: ");
    31.         for(Object e : tree){
    32.             System.out.print(e + " ");
    33.         }
    34.     }
    35.  
    36.     public static void printTree(BST tree){
    37.         System.out.print("\nInorder (sorted) : ");
    38.         tree.inorder();
    39.         System.out.print("\nPostorder : ");
    40.         tree.postorder();
    41.         System.out.print("\nPreorder");
    42.         tree.preorder();
    43.         System.out.print("\nThe number of nodes is " + tree.getSize());
    44.         System.out.println();
    45.     }
    46. }

    程序插入图示： 

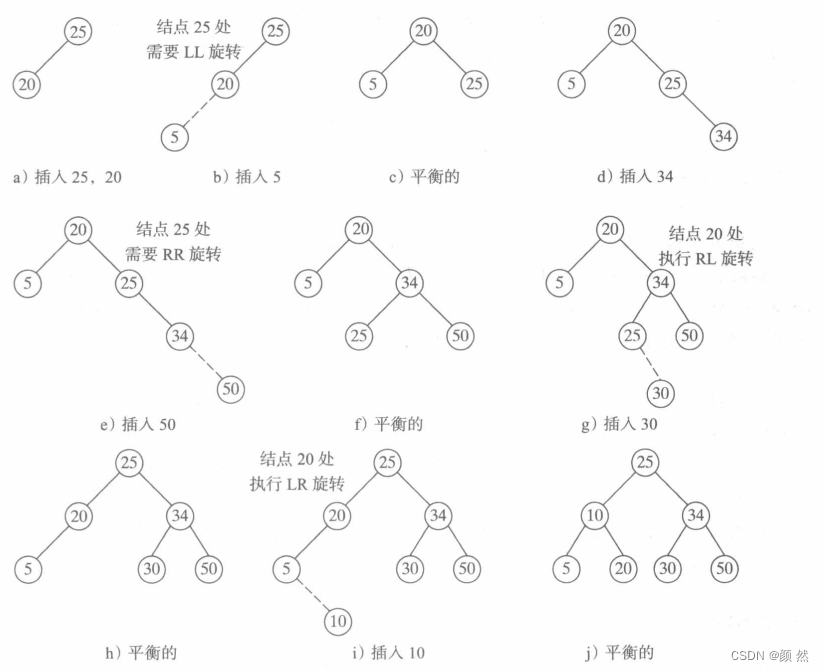
     程序删除图示：

  • 相关阅读:
    苹果注定要输给欧盟，USB-C成为标准接口已是大势所趋
    使用 GitHub Actions 通过 CI/CD 简化 Flutter 应用程序开发
    git常用命令
    Ubuntu 22.04 无法使用网易云音乐
    ecology集成中心hr同步的增量标识的意思
    【区块链 | Compound】3.剖析DeFi借贷产品之Compound：Subgraph篇
    WLAN 无线案例（华为AC控制器配置模板）
    第8天：可变与不可变类型、字典、元组与集合的内置方法
    基于FME Desktop和FME Server的数据增量自动更新
    [附源码]Python计算机毕业设计Django教学辅助系统
  • 原文地址：https://blog.csdn.net/Yan__Ran/article/details/125513921