思想

这个排序正好可以用到之前博文的master公式，这是一个mergeSort，整体思路也是递归行为。

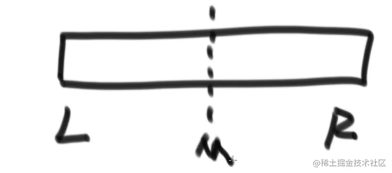
先让left数组排好序，再让right数组排好序，最后整合为一个有序数组。

关键的需要递归的整合算法：

先准备两个指针和一个辅助数组，分别指向左侧数组0位和右侧数组0位，然后compare，哪边更小就先拷贝哪一侧然后偏移一位，如果存在越界了，把另一侧都拷贝下来：

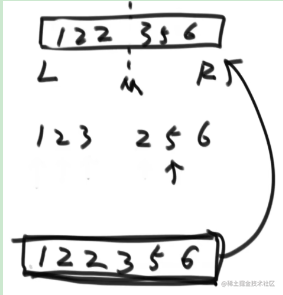
他的思想很重要，很多演化的题目，需要重点掌握

代码示例

public static void mergeSort(int[] arr){

    if(arr == null || arr.length < 2){

        return;

    }

    process(arr,0,arr.length-1);

}



public static void process(int[] arr,int L,int R){

    // 越界判断

    if(L==R){

        return;

    }

    // 获取中点

    int mid = L+ ((L+R) >> 1);

    // 左右排好序

     process(arr,L,mid);

    process(arr,mid+1,R);  

    // 整合

    merge(arr,L,mid,R);

}



public static void merge(int[] arr,int L,int M,int R){

    // 定义辅助数组和指向L和M+1的指针

    int[] help = new int[R-L+1];

    int i = 0;

    int p1 = L;

    int p2 = M+1;

    // 过程循环，两边都没有越界就循环，直到两侧有一侧越界 -> 结束后另一侧直接拷贝至辅助数组

    while(p1 <= M && p2 <= R){

        // 比较值，拷贝较小值至辅助数组并偏移

        help[i++] = arr[p1] <= arr[p2] ? arr[p1++]:arr[p2++];

    }

    while(p1 <= M){

        help[i++] = arr[p1++];

    }

    while(p2 <= R){

        help[i++] = arr[p2++];

    }

    // 辅助数组拷贝至目标 - 完成arr的L - R区间排序

    for(i=0;i < arr.length;i++){

        arr[L + i] = help[i];

    } 

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85

这里主要关注递归思想，还有通过两侧的++完成运算后自主偏移，还有辅助数组使用（存在排序操作避免影响原先数组）

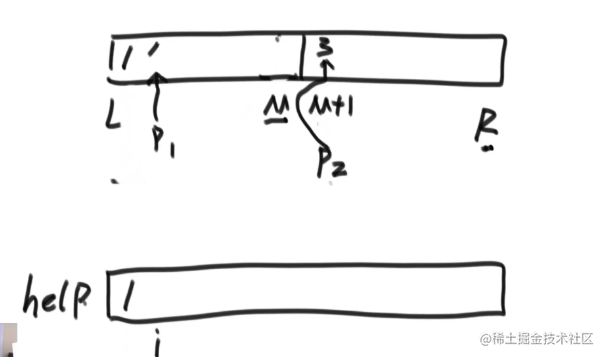
时间复杂度估计

接着尝试分析这个算法的时间复杂度，这里首先看看能不能套用master公式：

找到子问题，也就是两侧分别排序，这里a和b值都很好看，就是2

那么最后就是看merge操作的时间复杂度了：这里主要就是下标移动和compare赋值，其实是两个O(N)，最终还是O(N)复杂度

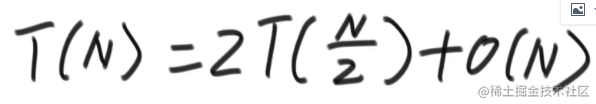
最终基于master公式log2^2 == d(1) -> O(N*logN)

为什么可以是NlogN复杂度？

它比之前的排序好在哪里呢？之前只是公式的结果，如何去理解复杂度的进步呢？

之前的选择，冒泡，插入都是N^2的算法，归根到底是因为他们浪费了很多次的比较结果，0-N数组需要比较N次才得到谁应该放在0位置上，接着1-N也比较了N-1次才搞定了1个数字到1位置。 – 每一轮比较都是独立的，很多相关比较信息都丢弃了，但是其实这些比较行为是有关系的

而归并排序则利用了比较的信息，这个信息成为了整体有序的部分，然后下一轮就是这个小部分和大部分比较，而比较信息是成功不断传递下去了，没有浪费！

总结