在线负载离线负载与在线算法离线算法

在线负载离线负载与在线算法离线算法

在研究生读研确定了要做调度以来，我一直困惑的一个问题是：什么是在线算法，什么是离线算法，中间弄清楚无数次，也迷茫了无数次（可能是因为我这个人比较蠢，老是会怀疑自己曾经学到的东西），后来看文献也看了很多离线算法和在线算法，直到一天看了这篇文章，我彻底区分开了离线算法和在线算法的区别。
其实谈到这两种算法就涉及了两种工作负载，在线负载和离线负载。
参考文献:在离线混部作业调度与资源管理技术研究综述
在文中是这样定义的：
在线作业
在线作业通常是以服务形态来处理用户请求并执行计算任务,如网页搜索服务、在线游戏服务、电商交易服务等,具备较高的实时性和稳定性需求.
由于要求实时，所以通常会留有大量的空闲资源。
运行时间长.在线作业通常以服务的形态持续运行,以请求(request)为单位触发计算任务.运行往往持续数周甚至数月,因此在线作业也被称为长服务(long runing service)
资源使用呈现动态变化.在线作业的资源使用量与用户并发请求量呈正相关,会伴随用户并发请求量发生动态变化.
对性能变化敏感.在线作业的性能通常决定了企业对外服务质量,而服务质量则直接影响企业的经济利益和用户体验.
离线作业
通常是计算密集型的批处理作业,如 MapReduce和 Spark 作业数据分析作业/机器学习模型训练作业等.多数离线作业对于性能没有严格的要求,可以容忍较高的运行延迟并支持失败任务的重启。
运行时长较短.离线作业运行时长大多位于数分钟到数小时这一区间.因此,与运行持续数周甚至数月的在线作业相比,离线作业的运行时长较短.
计算密集.离线作业通常需要进行大量的计算操作,深度学习模型训练作业也是典型的离线作业,此类作业通常需要进行大量的梯度计算,并且通过多次迭代直至模型收敛.
对性能变化不敏感.离线作业通常为批处理作业,对于性能没有严格的要求,可以容忍较大的运行延迟并支持任务的失败重启.
后来我又去看了百度的在离线混部以及分析了阿里集群数据集，我做了如下表格：

其中从阿里数据集分析发现，对于在线作业而言，假定该作业总共有10个容器需要部署，但是在该作业刚到达的时候可能只部署其中7个容器会不定期到达，而且调度系统是不知道它是什么时候会来，也不知道它的容器类型的，所以对于这一类的情况，但离线负载就不一样，它更多的是呈现出一种DAG图的形式，然后它是一起到的，所有数据对于你来说都是已知的，所以针对这两类作业的算法设计就出现不同情况。
在线算法：它可以以序列化的方式一个个的处理输入，也就是说在开始时并不需要已经知道所有的输入
离线算法：在开始时就需要知道问题的所有输入数据，而且在解决一个问题后就要立即输出结果。
看不懂？没关系，先看一篇文献压压惊
参考文献:Joint Optimization of Operational Cost and Performance Interference in Cloud Data Centers

系统模型

将云数据中心建模成无向图 ，
其中M( )表示物理服务器集合
L：服务器的物理链路的集合
s：服务器资源类型
资源集合： R i = { C i k }    { k = 1 , 2 , . . . , s } R_i=\left\{ C_{ik} \right\} \ \ \left\{ k=1,2,...,s \right\} Ri​={Cik​}  {k=1,2,...,s}
功耗与cpu利用率存在线性关系：
$$P\left[u\left(t\right)\right]=P_{\text{idle}}+\left(P_{\text{peak}}-P_{\text{idle}}\right)\ast u\left(t\right)$$
空闲功率 与cpu满载的情况下的功率
实例向量 :
I j = { a j , p j , R j } I_j=\left\{ a_j,p_j,R_j \right\} Ij​={aj​,pj​,Rj​}
其中aj表示到达时间，pj表示VMj单独运行，容量（资源）资源向量Rj
定义性能退化因子：$d_{jj}$
性能下降计算见算法方面
成本定义：
$$c_i\left(t\right)=P\left[u\left(t\right)\right]\tau$$
$$C_i\left(t\right)=\sum _i{c}_i\left(t\right)$$
虚拟机 的执行时间为：
$$t_j=t-a_j,t_j\ge p_j$$
则可以求解出自然损失（干扰损失）模型：
$$f\left[\left(\frac{t_j-p_j}{p_j}\right)\right]={\alpha }^{\left(\frac{t_j-p_j}{p_j}\right)}-1$$
$\alpha$是一个参数，其中 $\left(t_j\ge p_j\right)$
模型：
最小化成本与性能下降：

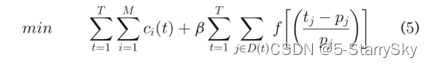
确保多个VM的聚合资源需求不会超过所有资源类和所有时间的服务器容量

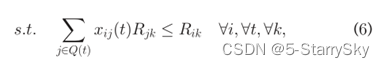
确保每个VM在任何时间点都分配给一个服务器

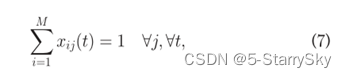
确保如果VM分配到服务器上，则不会将其分配给其他服务器

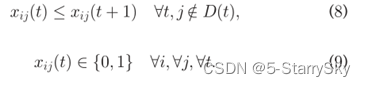
离线调度算法设计

装箱变异算法（BPV）
将虚拟机保存在一个列表中，按照到达时间的递增顺序排序。每个VM根据列表顺序分配给第一个可能容纳的服务器，并在发生容量冲突时调用服务器。虚拟机在完成工作后将离开服务器，相关资源将被恢复。
最小增加成本算法（MIC）
虚拟机也按到达时间的先后顺序排列。该算法将下一个VM分配给服务器，使总成本的增量最小化。下一个VM的分配有两种选择。当虚拟机被分配给运行现有虚拟机的活动服务器时，总成本的增量是能耗和性能下降惩罚的总和。另一种选择是当前未使用的服务器，假设VM进程单独运行，则需要支付更多的静态能耗。



对于以上这两种算法，排除排序阶段时，可以将其修改为在线算法。请注意，当一个虚拟机被分配给服务器时，必须更新该虚拟机自身的持续时间以及受其干扰的其他虚拟机的持续时间。
看到这里是不是对在线算法和离线算法清楚了很多，同时我们这里引用网上一个例子来说明：
选择排序是不断地从未排序的元素中找到最大（小）的元素放到排序序列的起始位置。

插入排序是不断将未排序的序列插入到有序的序列中，有序序列中的元素相对位置会在一定程度上被改变。
这里选择排序是离线算法，而插入排序是在线算法。