参考论文：Graph Attention Networks

一.前言

GAT（图注意力网络）是GNNs中重要的SOTA模型，该模型是从空域角度来进行定义，能够用消息传递范式来进行解释。GAT与GCN最大的不同便是它在图节点邻域聚合的过程中引入了注意力机制来计算邻居对当前正在聚合的节点的重要程度。本文的内容包括：图注意力网络的架构介绍、基于PyG来复现GAT模型。

二.GAT架构介绍

正如第一节中介绍的那样，GAT最大的贡献便是将注意力机制引入到图卷积中来，下面先给出该模型的架构图：

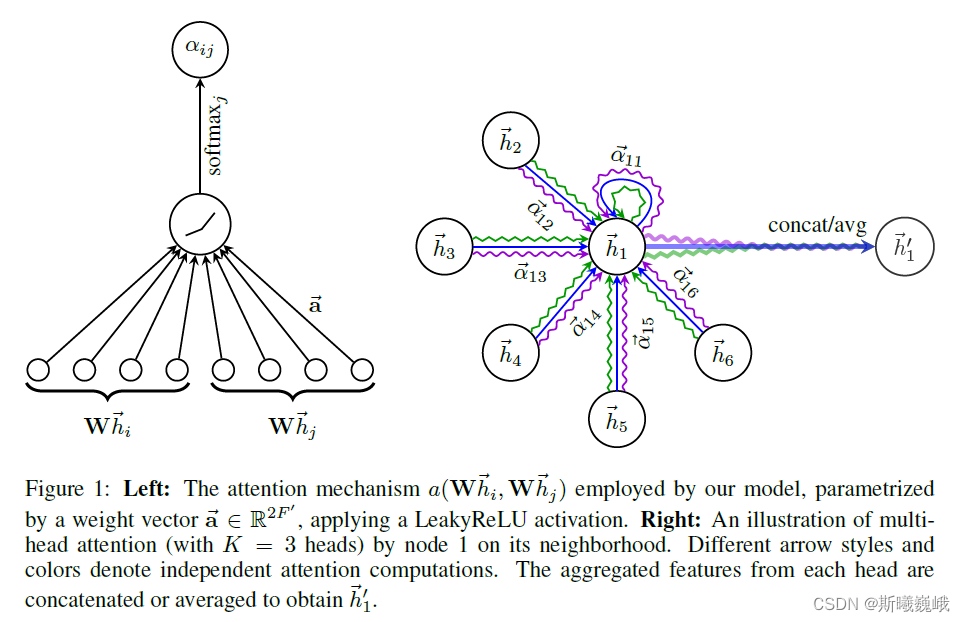
从该图可以看出，GAT在聚合过程中，需要计算1阶邻居节点对当前节点的重要程度，即${\vec{\alpha }}_{ij}$，然后进行加权求和。下面是该模型对应的消息传递范式的数学形式：
h i ( l + 1 ) = ∑ j ∈ N ( i ) α i , j W ( l ) h j ( l ) α i j l = softmax ⁡ j ( e i j l ) = exp ⁡ ( e i j l ) ∑ k ∈ N i exp ⁡ ( e i k l ) e i j l = L e a k y R e L U ( a ( W h i ( l ) ∥ W h j ( l ) ) )

hi(l+1)​αijl​eijl​​=j∈N(i)∑​αi,j​W(l)hj(l)​=softmaxj​(eijl​)=∑k∈Ni​​exp(eikl​)exp(eijl​)​=LeakyReLU(a(Whi(l)​∥Whj(l)​))​
其中$h_i^{(l)}$和$h_j^{(l)}$是GAT模型中第$l$层的节点特征，$a$是一个单层前馈神经网络，$\Vert$表示向量的拼接操作，$W$是权重矩阵，$\mathcal{N}(i)$表示节点$i$的1阶邻域。

另外，作者在论文中使用了多头注意力（Multi-Head Attention）机制，即可以将上述聚合公式扩展为如下形式：
$$h_i^{(l+1)}={\Vert }_{k=1}^K\sigma \left(\sum _{j\in {\mathcal{N}}_i}{\alpha }_{ij}^k{\mathbf{W}}^k{h}_j^{(l)}\right)$$
其中$K$表示注意力头的个数。

需要注意的是，若在最后一层使用多头注意力机制，则使用求平均来代替拼接操作，即：
$$h_i^{(l+1)}=\sigma \left(\frac{1}{K}\sum _{k=1}^K\sum _{j\in {\mathcal{N}}_i}{\alpha }_{ij}^k{\mathbf{W}}^k{h}_j^{(l)}\right)$$

三.复现工作

3.1 复现GAT模型

对于GAT模型，本文采用PyG来对其进行复现操作。若对PyG中如何实现消息传递神经网络不怎么了解的可以参见博主之前的博文《PyG教程(6)：自定义消息传递网络》。

GAT模型包含两个图注意力卷积层的GAT，两个卷积层之间的非线性激活为ELU，该模型的实现源码如下：

import torch
import torch.nn as nn
import torch.nn.functional as F
from torch_geometric.nn import MessagePassing
from torch_geometric.utils import softmax, add_remaining_self_loops


class GATConv(MessagePassing):
    def __init__(self, in_feats, out_feats, alpha, drop_prob, num_heads):
        super().__init__(aggr="add")
        self.drop_prob = drop_prob
        self.num_heads = num_heads
        self.out_feats = out_feats // num_heads
        self.lin = nn.Linear(in_feats, self.out_feats *
                             self.num_heads, bias=False)
        self.a = nn.Linear(2*self.out_feats, 1)
        self.leakrelu = nn.LeakyReLU(alpha)

    def forward(self, x, edge_index):
        edge_index, _ = add_remaining_self_loops(edge_index)
        # Wh
        h = self.lin(x)
        h_prime = self.propagate(edge_index, x=h)
        return h_prime

    def message(self, x_i, x_j, edge_index_i):
        x_i = x_i.view(-1, self.num_heads, self.out_feats)
        x_j = x_j.view(-1, self.num_heads, self.out_feats)
        # a(Wh_i, Wh_j)
        e = self.a(torch.cat([x_i, x_j], dim=-1)).permute(1, 0, 2)
        # LeakReLU(a(Wh_i, Wh_j))
        e = self.leakrelu(e.permute(1, 0, 2))
        # softmax(e_{ij})
        alpha = softmax(e, edge_index_i)
        alpha = F.dropout(alpha, self.drop_prob, self.training)
        return (x_j * alpha).view(x_j.size(0), -1)


class GAT(nn.Module):
    def __init__(self, in_feats, hidden_feats, y_num,
                 alpha=0.2, drop_prob=0., num_heads=[1, 1]):
        super().__init__()
        self.drop_prob = drop_prob
        self.gatconv1 = GATConv(
            in_feats, hidden_feats, alpha, drop_prob, num_heads[0])
        self.gatconv2 = GATConv(
            hidden_feats, y_num, alpha, drop_prob, num_heads[1])

    def forward(self, x, edge_index):
        x = self.gatconv1(x, edge_index)
        x = F.elu(x)
        x = F.dropout(x, self.drop_prob, self.training)
        out = self.gatconv2(x, edge_index)
        return F.log_softmax(out, dim=1)


if __name__ == "__main__":
    conv = GATConv(in_feats=64, out_feats=64, alpha=0.2,
                   num_heads=8, drop_prob=0.2)
    x = torch.rand(4, 64)
    edge_index = torch.tensor(
        [[0, 1, 1, 2, 0, 2, 0, 3], [1, 0, 2, 1, 2, 0, 3, 0]], dtype=torch.long)
    x = conv(x, edge_index)
    print(x.shape)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65

3.2 实验

3.2.1 实验数据集

本文以Cora数据集为例进行实验，该数据集为一个论文引用网络，包含了2708篇论文，每篇论文都由1433维的词向量表示。该论文引用网络包含5429条边，表示论文间的引用关系。数据集中的论文分为7个类别。

3.2.2 超参配置

本文实验的超级参数来源于GAT论文，具体如下表所示：

3.2.3 实验结果展示

在实验过程中，使用训练集进行模型的参数更新，然后使用验证集来筛选最佳的模型，最后将最佳的模型在测试集上进行测评。某次实验的运行结果截图如下：

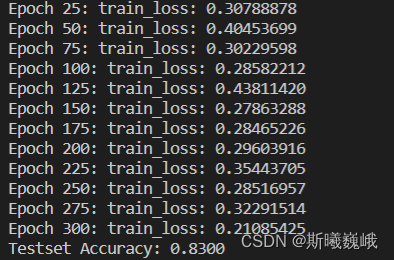
从最后的结果来看，和论文里面的报的相应数据集的结果差不多。当然，限于时间原因，没有细致调参和做一些可视化相关的工作，有感兴趣的小伙伴可以自行研究。

四.结语

完整项目Github地址：GAT
以上便是本文的全部内容，要是觉得不错的话就点个赞或关注一下博主吧，你们的支持是博主继续创作的不解动力，当然若是有任何问题也敬请批评指正！！！