堆 AcWing 838. 堆排序

原题链接

AcWing 838. 堆排序

算法标签

堆

思路

堆的本质

完全二叉树

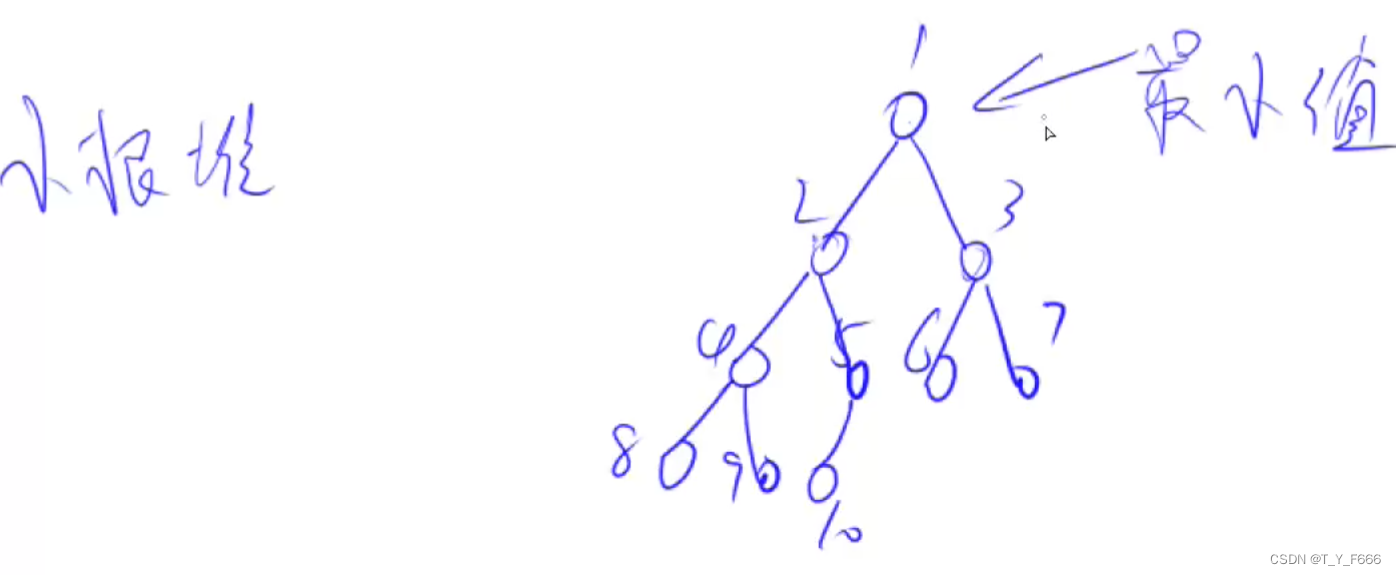
常见的堆

小根堆 根节点存储最小值， 左右节点存储值大于根节点
大根堆 根节点存储最大值， 左右节点存储值小于根节点

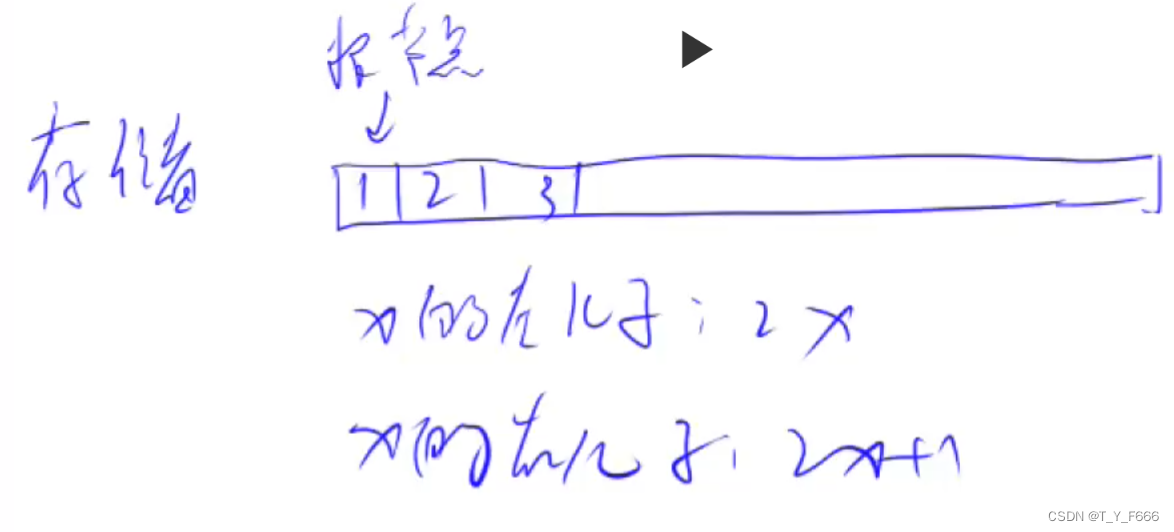
存储方式
采用一维数组存储 。注意： 此处数组下标从1开始
若从0开始，则根节点会被根节点左儿子覆盖

堆的基本操作

down操作 将当前节点与左右儿子比较， 若当前节点 > 左右儿子中较小值, 将当前节点与左右儿子中较小值位置交换，交换后递归进行上述操作，直至找到适合的位置
up操作 将当前节点与根节点比较， 若当前节点 < 根节点, 将当前节点与根节点位置交换，交换后递归进行上述操作，直至找到适合的位置
为了保证堆结构的稳定性，对于插入与删除操作， 选择在数组尾部进行操作

堆的基本操作伪代码

堆的构建

若依次从尾部插入，每次插入时间复杂度log(n), 需要插入n个元素， 时间复杂度n*log(n)
若依次从N/2插入，可以保证在O(n)的时间复杂度内插入n个元素
证明过程

代码

#include<bits/stdc++.h>
#define int long long
#define rep(i, a, b) for(int i=a;i<b;++i)
#define Rep(i, a, b) for(int i=a;i>b;--i)
using namespace std;
const int N = 100005;
// p存储节点祖宗节点 s存储所属连通块节点数
int a[N];
int s;
inline int read(){
   int s=0,w=1;
   char ch=getchar();
   while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
   while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
   return s*w;
}
void put(int x) {
    if(x<0) putchar('-'),x=-x;
    if(x>=10) put(x/10);
    putchar(x%10^48);
}
// 选取左右节点较小值
void down(int x){
    int u=x;
    if(x*2<=s&&a[x*2]<a[u]){
        u=x*2;
    }
    if(x*2+1<=s&&a[x*2+1]<a[u]){
        u=x*2+1;
    }
    if(x!=u){
        swap(a[x], a[u]);
        down(u);
    }
}
signed main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int n=read(), m=read();
    s=n;
    rep(i, 1, n+1){
        a[i]=read();
    }
    Rep(i, n/2, 0){
        down(i);
    }
    while(m--){
        printf("%lld ", a[1]);
        a[1]=a[s--];
        down(1);
    }
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54

原创不易
转载请标明出处
如果对你有所帮助 别忘啦点赞支持哈