参考文章：
https://zhuanlan.zhihu.com/p/117634492

1 欧式距离与DTW的比较

DTW更加适合在时间轴上有伸缩的情况，在语音序列匹配中使用广泛。

• 欧式距离：是一种常用的 “ 点距离 ” 的度量方法。计算的是同一时刻上点的距离之和。
• DTW距离：允许时间点的 “扭曲” ，而且，可以存在一个点对应多个点和多个点对应一个点的情况。也就是说，每个点都尽可能地找离它最近、距离最小的带你，允许时间轴上的压缩。

2 DTW 的思想

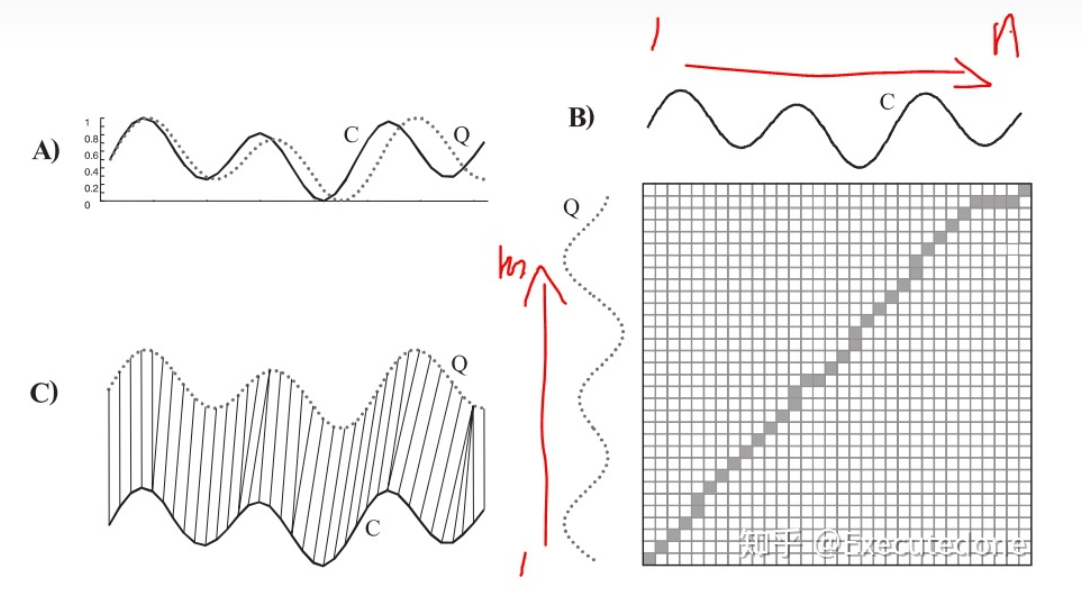
• 注意一下，二维数组 m×n 里面存放的值，比如说是 [i, j] 应该是序列a中第i个值和序列b中第j个值的距离。
• 这个距离的度量有很多，可以是欧式距离，可以是下面文字中说明的平方差，总之要根据应用背景来确定。
  

2.1 DTW的特点

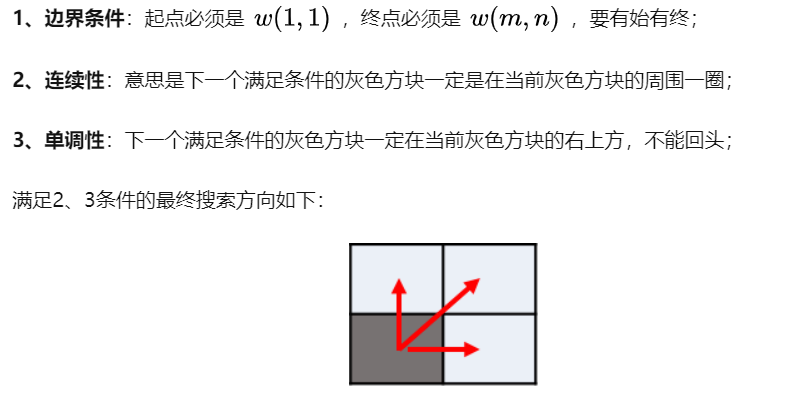
2.2 DTW 的思想步骤

假设：
（1）有序列a长度为m
（2）有序列b长度为n
（3）m×n 的矩阵 叫做d[ ][ ]
（4）这里定义两个点之间的距离，就是差的绝对值，叫做fun()

1. 计算d[0][0] = fun(a[0], b[0])

2. 计算第0行
   d[i][0] = fun(a[i],b[0])

3. 计算第0列
   dp[0][j] = fun(a[0],b[j])

4. 计算剩余的值：选择{左边、上边、左上角}三个值中最小的值 + fun (a[i], b[j] )
   d[i][j] = min(d[i-1][j-1],d[i-1][j],dd[i][j-1]) + fun(a[i],b[j])

3 举例说明

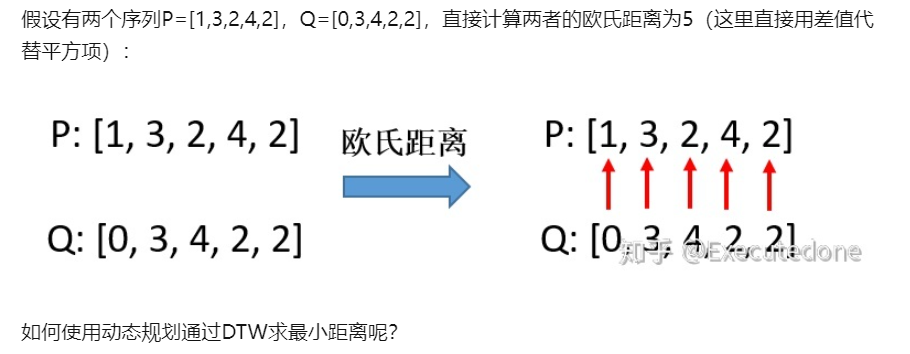
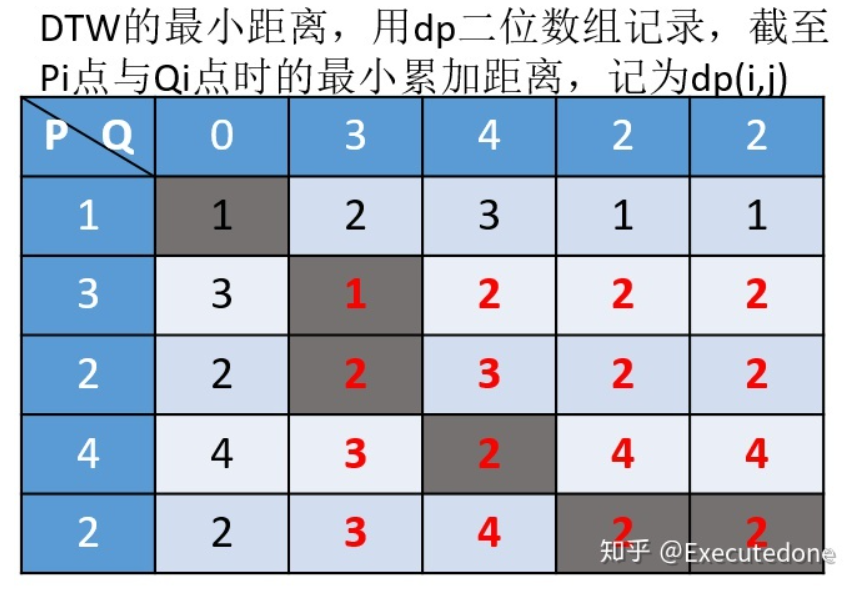
4 代码

# 计算序列组成单元之间的距离，可以是欧氏距离，也可以是任何其他定义的距离,这里使用绝对值
def distance(w1,w2):
    d = abs(w2 - w1)
    return d

# DTW计算序列s1,s2的最小距离
def DTW(s1,s2):
    m = len(s1)
    n = len(s2)

    # 构建二位dp矩阵,存储对应每个子问题的最小距离
    dp = [[0]*n for _ in range(m)] 

    # 起始条件,计算单个字符与一个序列的距离
    for i in range(m):
        dp[i][0] = distance(s1[i],s2[0])
    for j in range(n):
        dp[0][j] = distance(s1[0],s2[j])
    
    # 利用递推公式,计算每个子问题的最小距离,矩阵最右下角的元素即位最终两个序列的最小值
    for i in range(1,m):
        for j in range(1,n):
            dp[i][j] = min(dp[i-1][j-1],dp[i-1][j],dp[i][j-1]) + distance(s1[i],s2[j])
    
    return dp[-1][-1]

s1 = [1,3,2,4,2]
s2 = [0,3,4,2,2]

print('DTW distance: ',DTW(s1,s2))   # 输出 DTW distance:  2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30