-
时间复杂度与空间复杂度
我们在讨论算法的时候,面试的时候,甚至刷题的时候都要逃不过的一点,就是让我么你主要算法的时间复杂度和空间复杂度。一般来说时间和空间不可兼得,当我们内存固定,可能我们就需要牺牲时间去换取空间,但是现在随着计算机的发展,内存的上限不在被我们过多的考虑。在高并发环境下,我们更多的是去考虑用户的使用体验,也就是用户可以用更少的时间去获取自己想得到的数据,也就是用空间换取时间。所以对于时间复杂度的分析也是代码review的意一项要参考。
时间复杂度:
算法的时间复杂度,是一个用于度量一个算法的运算时间的一个描述,本质是一个函数,根据这个函数能在不用具体的测试数据来测试的情况下,粗略地估计算法的执行效率,换句话讲时间复杂度表示的只是代码执行时间随数据规模增长的变化趋势。
T(n)和O(n):
我们常用O来表示算法执行的增长速度,读作大oh,n是输入数据的大小或输入数据的数量,算法需要执行的运算次数我们一般使用T(n)来表示。我们假设存在常数c和函数f(n),使得当 n >= c
时
 ,记作
,记作  ,这个公式的全称是:算法的渐进时间复杂度。
,这个公式的全称是:算法的渐进时间复杂度。举个例子,看看以下的代码 :
- /**
- * @author Zeyu Wan
- * @version 1.0.0
- * @ClassName dsfasfs.java
- * @Description TODO
- * @createTime 2022年06月01日 15:23:00
- */
- public class bigOh {
- public static void main(String[] args) {
- func1();
- func2(12);
- }
- public static void func1(){
- System.out.println("打印了");
- }
- public static void func2(int n){
- for (int i = 0; i <n ; ++i) {
- System.out.println("打印了");
- }
- }
- }
T(n):
针对 func1() 这个方法:
执行的时候值打印了一次,所以我们可以说T(n)=1.
针对 func2() 这个方法:
我们看到这个for循环进行分析:
1. 我们传入的数值是12:
2. 初始化int i =0 执行了一次
3. 然后对应i<12,我们执行了13次判断,从i=0 到 i=12,最后一次是i=12的时候。
4. ++i 执行了12次
里面的print函数执行了12次。
总计一下,这个算法的
 ,我们把情况泛化,假设传入函数的n就是n次:
,我们把情况泛化,假设传入函数的n就是n次:
所以我们可以发现,当代码量多的时候,T(n)表示法就会非常的复杂,所以引出了大O表示法来简化T(n)的估算值,衡量代码的执行速度:这个简化的估算值叫做时间复杂度
O(n):
那么对应 func1() 函数,T(n)的值为常数,我们就可以直接估算为 1,所以我们一般使用O(1)表示常量阶。
O(1)的意思就是代码在执行的时候,它消耗的时候并不随着某个变量的增长而增长,那么无论这类代码有多长,即使有几万几十万行,所有的代码都只会执行一遍,所以用O(1)来表示它的时间复杂度。
那么对于我的个人理解而言,就是不论n的值是什么,总会存在一个 M*1+C 的函数曲线成为T(n)的上限。
对于func2()函数,T(n)=3n+2,我们可以发现,函数的循环次数与n正相关,n越大函数循环次数越多,那么时间复杂度越大。简化函数也就是O(n),也就是就是不论n的值是什么,总会存在一个M*n+C的函数曲线成为T(n)的上限。
我们已知:


所以当n->∞的时候,我们对于函数增长的变化趋势可以忽略他的常数项和他的常数系数,而关注于n的幂次数本身。
由此可以看出,大O符号表示法并不是用于来真实代表算法的执行时间的,它是用来表示代码执行时间的增长变化趋势的。我们考虑的是当n趋近于无穷大的时候,T(n)中的常量与常数倍数是没有意义的。
由此我们可以做出一个简单的归纳:
名称 时间复杂度 常数时间 
对数时间 
线性时间 
线性对数时间 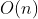
二次时间 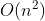
三次时间 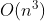
指数时间 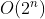
上面从上至下依次的时间复杂度越来越大,执行的效率越来越低。
1. 常数阶:
无论代码执行了多少行,只要是没有循环等复杂结构,那这个代码的时间复杂度就都是O(1)
一般来说普通的加减法,不涉及循环,或者是变量赋值等,我们都只考虑他的O是1,它消耗的时间并不随着某个变量的增长而增长。如:
- int i = 1;
- int j = 1;
- ++i;
- j++;
- int m = i + j;
2. 线性阶:
常见的线性阶就是单层的for循环,循环次数和n有关。对于循环代码:
- for(i=1; i<=n; ++i)
- {
- j = i;
- j++;
- }
循环会执行n次,所以可以用O(n)表示时间复杂度
3. 对数阶:
对于代码:
- int i = 1;
- while(i<n)
- {
- i = i * 2;
- }
在循环中,每一次i都会*2,也就是2的x次方就等于n,那么x=log_2n , 也就是再循环了log_2n次后循环结束,我们就可以视为这个代码的时间复杂度是O(logn).
4. 线性对数阶:
对于代码:
- for(m=1; m<n; m++)
- {
- i = 1;
- while(i<n)
- {
- i = i * 2;
- }
- }
也就是基础的两层n阶循环嵌套,由此之上我们可以更加的泛化:
- for(x=1; i<=m; x++)
- {
- for(i=1; i<=n; i++)
- {
- j = i;
- j++;
- }
- }
那对于上面的代码,时间复杂度就变成了O(m*n)
6. 立方阶:
也就是在平方阶基础上n层循环。就是O(n*n*n*n)
分析分析:
时间复杂度计算专题_程序员 DELTA的博客-CSDN博客_时间复杂度计算
空间复杂度:
如果我们理解了时间复杂度,那么对于空间复杂度也会有了一个基础的认识。空间复杂度是对一个算法在运行过程中临时占用存储空间大小的一个量度,同样反映的是一个趋势,我们用 S(n) 来定义。
和时间复杂度一样,空间复杂度一般常见的有:

1. 常数阶:
普通常量、变量、对象、元素数量与输入数据大小 N 无关的集合,皆使用常数大小的空间。
尤其注意如下代码:
- void forLoop(int n) {
- for (int i = 0; i < n; i++) {
- test();
- }
- }
虽然函数 test() 调用了 N 次,但每轮调用后 test() 已返回,无累计栈帧空间使用,因此空间复杂度仍为 O(1) 。
2. 线性阶:
元素数量与 N 呈线性关系的任意类型集合(常见于一维数组、链表、哈希表等),皆使用线性大小的空间。
值得注意的是对于如下递归调用:
- int rec(int n) {
- if (n <= 1) return 1;
- return rec(n - 1) + 1;
- }
递归调用期间,会同时存在 n 个未返回的 rec() 函数,因此使用 O(n) 大小的栈帧空间。
3. 平方阶:
元素数量与 N 呈平方关系的任意类型集合(常见于矩阵),皆使用平方大小的空间。
- int rec(int N) {
- if (N <= 0) return 0;
- int nums[N];
- return rec(N - 1);
- }
递归调用时同时存在 N 个未返回的 rec() 函数,使用 O(N) 栈帧空间;每层递归函数中声明了数
组,平均长度为
 , 使用 O(N) 空间;因此总体空间复杂度为
, 使用 O(N) 空间;因此总体空间复杂度为 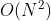 。
。4.指数阶:
指数阶常见于二叉树、多叉树。例如,高度为 N 的「满二叉树」的节点数量为
 ,占用
,占用
大小的空间;同理,高度为 N 的「满 m 叉树」的节点数量为
 ,占用
,占用 大小的空间。
大小的空间。5.对数阶:
对数阶常出现于分治算法的栈帧空间累计、数据类型转换等,例如:
1)快速排序 ,平均空间复杂度为
 ,最差空间复杂度为 O(N) 。通过应用 Tail Call Optimization ,可以将快速排序的最差空间复杂度限定至 O(N)。
,最差空间复杂度为 O(N) 。通过应用 Tail Call Optimization ,可以将快速排序的最差空间复杂度限定至 O(N)。2)数字转化为字符串 ,设某正整数为 N ,则字符串的空间复杂度为 O(logN) 。
推导如下:正整数 N 的位数为
 ,即转化的字符串长度为
,即转化的字符串长度为  ,因此空间复杂度为
,因此空间复杂度为 
常见排序的时空复杂度:
排序方式 平均时间复杂度 最坏时间复杂度 最好时间复杂度 空间复杂度 稳定性 备注 快速排序 
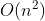


不稳定 最坏比较次数: 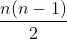
归并排序 


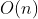
稳定 堆排序 



不稳定 冒泡排序 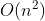
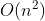
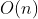

稳定 最坏比较次数: 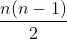
选择排序 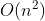
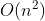
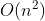

不稳定 插入排序 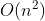
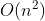
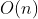

稳定 最坏比较次数: 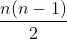
希尔排序 
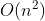

不稳定 基数排序 



稳定 d为位数,r为基数 计数排序 



稳定 k是整数的范围 参考:
什么是时间复杂度_MorKANA的博客-CSDN博客_时间复杂度
时间复杂度计算专题_程序员 DELTA的博客-CSDN博客_时间复杂度计算
空间复杂度_吕同学的头发不能秃的博客-CSDN博客_空间复杂度
-
相关阅读:
9.基于粤嵌gec6818开发板小游戏2048的算法实现
【校招VIP】“推推”项目课程Java:SpringBoot demo的说明、入门和下载
知乎二面:请问Redis 如何实现库存扣减操作和防止被超卖?
Windows 安装mysql数据库
【mmdetection】ROIExtractor中的featmap_strides和finest_scale
Oracle事务
C++提高编程
如何提升Java项目质量,代码是关键
【初阶数据结构】树(tree)的基本概念——C语言
8051(c51)单片机从汇编到C语言,从Boot到应用实践教程
- 原文地址:https://blog.csdn.net/m0_56289903/article/details/125521011
