-
课程设计书五子棋AI算法及其实现
五子棋AI,能根据棋盘局势判断棋子应落在何处获胜,主要算法有权值法和博弈树法两种实现方案。
权值法
在数理统计中,有一种名为蒙特卡洛法的方法常被使用,其主要内容为:根据事件出现的概率估计某些特征,并将其作为问题的解。 权值法实现五子棋AI利用的就是这个原理。在五子棋中,当棋局逐渐形成时,再接着向某个方向进行落子便容易获胜。比如黑子横向三连时,如果接着向左或者向右落子,白方不加堵截的话,那么黑方必胜。我们称此时棋盘上在黑子三连左右两侧的点的获胜概率高,即权值大。
对于黑方来说,在权值大的点上落子容易获胜,对于白方来说,在权值大的点上落子容易避免对方获胜。因而,无论对于哪方,在权值大的点上落子都是应该被优先选择的。
那么问题就变简单了,我们只需要对棋盘进行遍历,找出棋盘上权值大的点落子即可,利用这个方案,不仅可以实现人机对战,还可以实现机器与机器之间的博弈。
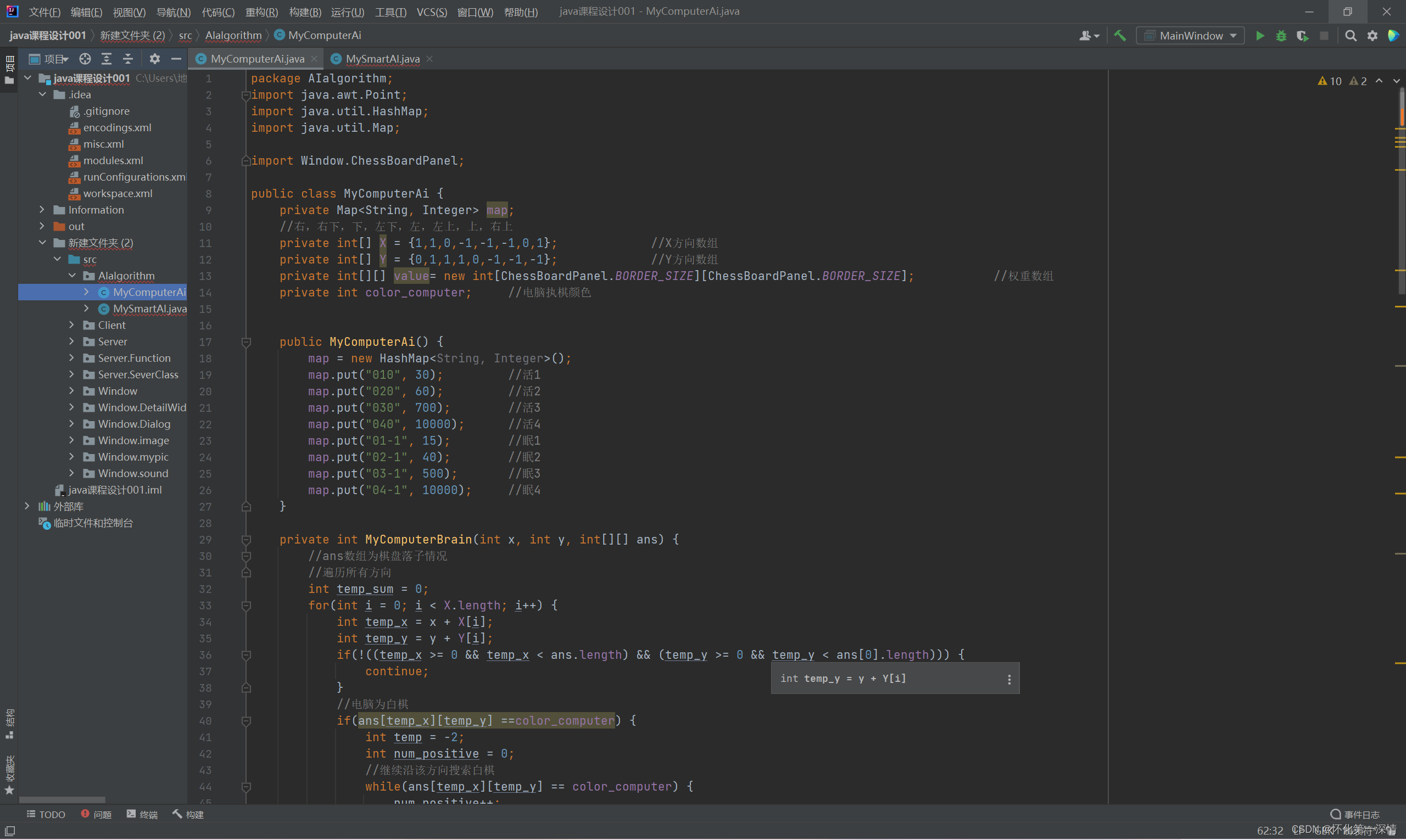
其中权值法用于简单人机写于MyComputerAi类中,通过不断递归循环上、下、左、右、左上、右上、左下、右下遍历整个棋盘找到权值最大点进行激活,其中主要运用数组x,y判断方向,以及权重数组以及map辅助判断这个点是否选择。
博弈树与极大极小值搜索
循序渐进,我们先考虑一步棋,如下图所示:假设在当前盘面下,我们有四种走法,对于每种走法我们调用上文的评估函数,得到四个得分,显然,我们更倾向于选择最高分15对应的那个走法。换句话说,我们可以认为以当前局面发展,可以到达15分的局面。
现在我们开始考虑两步棋,如下图所示:假设对于我的这四种走法,对方分别有两种走法进行应对。现在情况开始变得复杂了。我们重新强调一下,这是一个“零和博弈”,也就是说,我的正分一定等于对方的负分。如果我选择了15分这种走法,对方肯定不傻,一定会选择2分这种走法,想让我的分更低。如果我选择了10分这种走法,对方一定会选择5分这种走法。想要将局面变成6分或者8分的结果,是不可能的(除非对面犯傻)。那么对于图上的那种情况,我们分析一下:如果我选第一种走法,则会得到5分;如果我选第二种走法,则会得到2分;如果我选第三种走法,则会得到0分;如果我选第四种走法,则会得到1分。那我到底应该选择哪种走法呢?显然,我更希望两步棋后,局面是5分,我选择了第一种走法。
重新审视一下这个问题,我们不难发现,如果我考虑两步棋,那么第一步棋的得分是没有用的。我的实际求解过程是:先通过每种第一步棋,求得对应的第二步棋的最小得分,再从这些最小得分中,找到那个最大得分。
好了,为了游戏更加精确,我们继续尝试考虑4步棋。自己画图太过麻烦,我就随便搜索了一张图片:同样,按照上面的思路,我们需要反着考虑。首先考虑第四步棋,这是对方选择的一步棋。对于每一种第三步的局面,对方肯定选择分数最低的一步棋,我们把同一个第三步下的所有第四步的最小值求出来,作为第三步的分数即可。然后对于每个第二步的局面,我肯定选择分数最高的那个第三步,因此只需要求出同一个第二步下的所有第三步的最大值求出来,即可作为第二步的分数。同理,我们继续找第二步的最小值当做第一步的分数。最后再找到第一步的最大值,作为我决策的下一步棋。
以上,就是我们所说的“极小极大值搜索”算法。
值得一提的是,如果我优先下出了五连珠,游戏会立即结束,如果下一步棋对方也下出了五连珠,则我的五连珠调用减去对方的五连珠调用evaluateBoard(2)等于0,这个情况我们要排除掉,因为我已经先下出五连珠了,游戏已经结束了,对方再下出来的棋是无效的。

-
相关阅读:
Mysql主从复制数据一致性校验
postgresql 表、索引的膨胀率监控
【owt】vs2022 + v141 : 查看WINDOWSSDKDIR
【Python模块】logging 日志模块
阿里云Hologres助力好未来网校实时数仓降本增效
架设好传奇登录器显示无法连接服务器,完美登录器使用常见问题解决办法
Leet code 179 最大数
【OpenCV-Python】教程:3-11 图像变换(频域变换)
C Primer Plus(6) 中文版 第2章 C语言概述 2.3 简单程序的结构
3D成像技术概述
- 原文地址:https://blog.csdn.net/m0_66117547/article/details/125519709