-
干货丨浅谈足式机器人的运动控制
“
本期技术干货,我们邀请到了小米机器人实验室工程师——游洋威,来和大家从经典的三分控制法、零力矩点控制到目前主流的模型预观控制等方面,介绍足式机器人的运动控制。
”
一、前言
不论是非洲大草原上高速飞奔的猎豹,青藏高原上灵活跳跃的羚羊,还是万物之灵的人类自己,都无不让人惊叹造物主的鬼斧神工,也激发着人们梦想能有朝一日做出类似的人造物。诸葛亮的木牛流马,达芬奇的发条骑士,都是朝这个梦想前行的脚印。现代科技的高速发展,特别是机器人技术的日渐成熟,让这个梦想越来越贴近现实。虽然目前成熟的机器人技术和应用还主要集中在机械臂和轮式移动机器人上,但大部分人对机器人的第一印象还是像铁臂阿童木一样的仿生拟人的形态,相信也是很多机器人工程师的初心,这篇文章就给大家简单介绍下足式机器人的运动控制。

二、经典
>>>>(1)三分控制法
说到足式机器人,就算不是机器人圈的小伙伴,很多估计也看过Boston Dynamics公司的网红机器人BigDog, Atlas, Spot等等。这些机器人超强的稳定平衡能力和极佳的灵活运动性能让人眼前一亮。虽然Boston Dynamics作为受美国军方资助过的商业公司,对自己的技术守口如瓶,但他们的创始人Mac. Raibert早在80,90年代就已经在MIT Leg Laboratory利用液压驱动器做出了一批令人惊叹的足式机器人。

虽然Boston Dynamics公司现在的运动控制技术可能已经脱胎换骨大不一样了,但Mac. Raibert当时提出的三分控制法[1],还是非常简洁有效,很有启发借鉴意义的。具体来说,三分控制法将足式机器人的运动控制划分为三部分独立进行控制,比较常见的划分方式是:
利用着地腿的髋关节力矩控制机身姿态
利用着地腿的轴向出力调节机身高度
利用摆动腿的落脚点调节机器人的运动速度
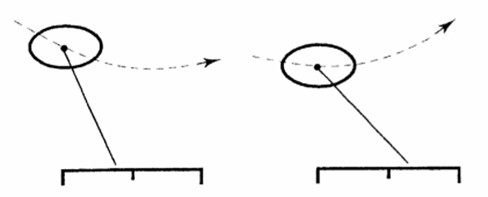
这个控制律人为地将机器人的六维位姿解耦分开,然后用类PID控制器进行控制,非常直观,是一种启发式方法。其中比较有意思的一点是通过落脚点调整机器人的运动速度,它利用了一个简单的原理:以稳定速度运行时,机器人着地和离地轨迹应该绕一个轴线对称,如果要加速脚应该踩在轴线的后方,反之应该前方,这个控制策略可以写成:
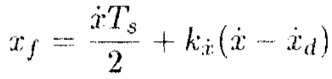
式中,xf是期望的足端相对机身的落足点,x'和xd'分别是当前速度和期望速度,Ts是着地时间,kx'是反馈系数。三分控制法的问题是没有利用模型信息,使用时需要大量繁琐的调参工作。除了前面提到的划分方法,还有利用着地腿的髋关节力矩控制运动速度,然后落脚点调节机身姿态等等其他划分方法,具体选择取决于应用场景。
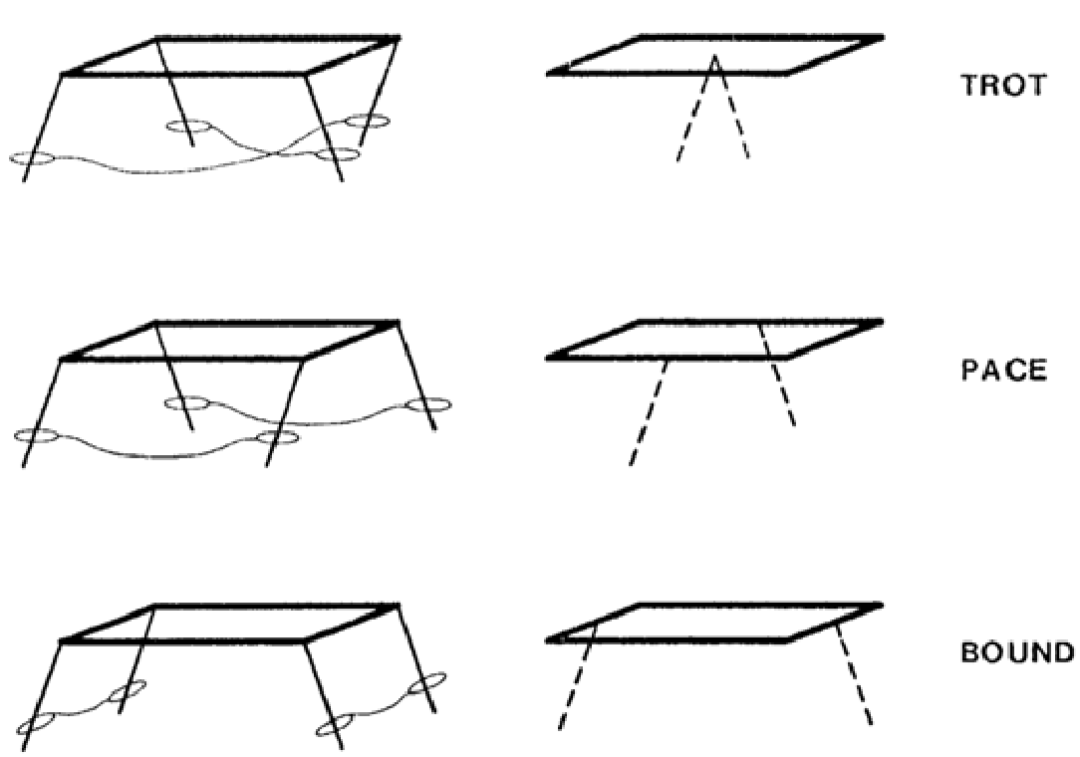
三分控制法可以直接应用在单腿和双足机器人上,在推广到四足及其他多足机器人时,经常会借用虚拟腿的概念,如下图。trot步态时将对角腿想象成一条过质心的虚拟腿,bound步态时将两条前腿或后腿想象成一条虚拟腿等等。
>>>>(2)虚拟模型控制
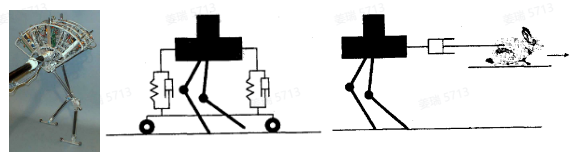
Mac. Raibert提出三分控制法的同时期,他在MIT的同事Jerry Pratt提出了基于雅克比矩阵的虚拟模型控制,成功实现了对一只类似鸵鸟的电机驱动的双足机器人的行走控制。虚拟模型控制的思路也非常直接朴素,首先将机器人的期望运动特性用一些物理概念来抽象代表以生成工作空间中期望的力和力矩,然后根据虚功原理将工作空间的力和力矩用雅克比矩阵映射成关节空间的力矩。这个方法和机械臂上广泛应用的阻抗控制有相近的地方,只是单纯用雅克比矩阵进行关节力矩映射忽略了惯量信息,在高速动态时可能跟踪不好影响运动性能。
>>>>(3)基于简化模型的零力矩点控制
90年代开始,本田公司在双足机器人上潜心研究,开发了一系列双足机器人,最终版的ASIMO广为认知,作为日本机器人外交的使者经常接待各国领导人,可爱的外形深受小朋友的喜爱。在ASIMO的背后是日本深厚的机器人文化和持续的研发投入,东京大学、东京工业大学、AIST等等在双足机器人领域都有深入的研究,也涌现了一批像Kajita(HRP机器人开发者)一样有影响力的机器人专家。他们常用的控制方法就是基于简化模型的零力矩点(ZMP)控制。
1972年,Vukobratovic和Stepanenko在一篇关于仿人机器人控制的论文中定义了ZMP的概念,它指的是足底所受合力在足底上的作用点。一个运动要是可实现的,得保证ZMP在支撑多边形内,这也就是足式机器人常用的稳定判据。
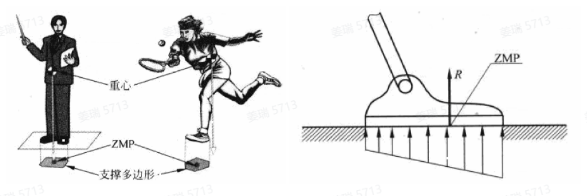
同时,机器人的整体运动可以通过一个单质点来表示,为简化计算,一般选用高度固定或有约束的线性倒立摆模型。
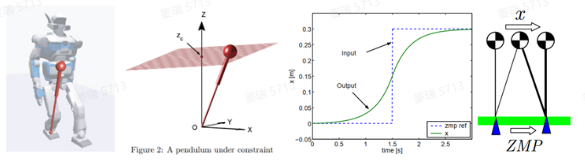
将线性倒立摆模型离散化,可以得到如下的系统方程:
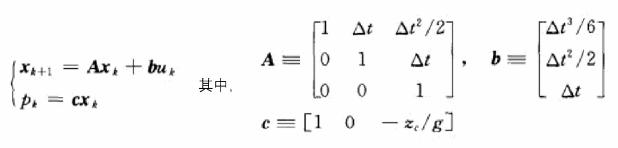
式中,状态量x是质心的位置、速度和加速度,输入量u是质心加速度的导数,跃度,输出量p是ZMP。通过选择合适的落脚点和在支撑多边形内调整ZMP点,我们可以根据ZMP稳定判据来计算最优的质心轨迹。假设,我们期望ZMP尽量靠近参照值,比如脚掌的中心,同时质心跃度输入尽量小,保证轨迹平滑,可设置目标函数(Q,R是目标权重系数)为:
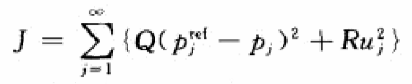
此时,我们可得到系统的最优输入解析解为:

其中矩阵P是下面Reccati方程的解:
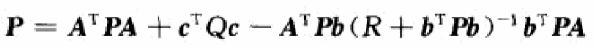
根据得到的质心轨迹和规划的摆动腿足端轨迹,通过逆运动学解算,我们可以得到各个关节的轨迹曲线,然后发送给关节驱动器进行跟踪伺服。由于模型误差和当时关节多采用高刚度位置伺服,踏步时地面冲击较大,为提高运动的稳定性,一般还需要步行稳定器,如通过踝关节力矩或质心加速度来实时调整ZMP位置等等。
>>>>(4)基于中枢模式发生器的运动控制
中枢模式发生器(CPG)是发现于无脊椎动物和脊椎动物中的一种神经网络,是实现许多节律行为的生物学基础。它能够在没有任何来自感觉反馈或更高控制中心的节奏输入的情况下,产生协调的节奏活动模式。不过,感官反馈虽然不是必需的,但它在运动受到环境扰动时保证动作协调稳定起着非常重要的作用。CPG可以产生发生周期性的振荡信号,用于控制机器人运动时,可以作为替代基于有限状态机、正弦发生器以及预设参考轨迹等方法的一种新方法。CPG中单个神经元的模型可以表示为:

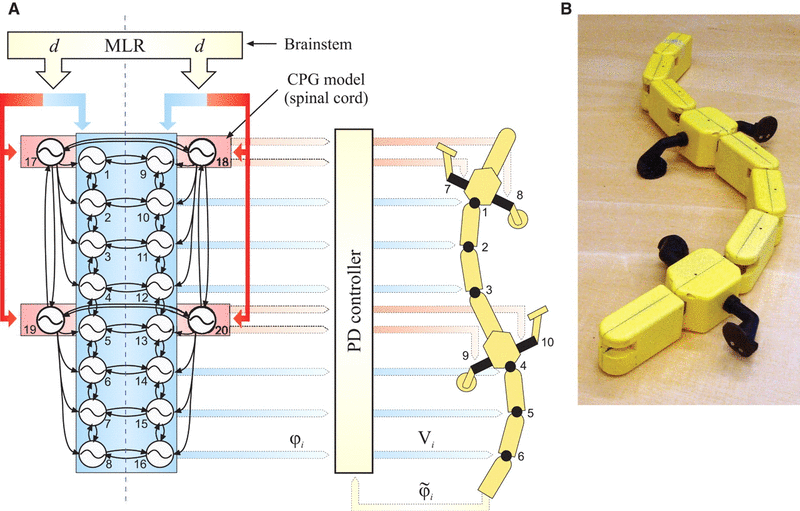
采用两个神经元的互抑模型可以组成如下面左图的关节振荡器,其中一个为伸肌神经元,另一个为屈肌神经元,两个神经元之间互相抑制,交替兴奋,其出状态合成为规律性振荡,可用于机器人关节运动控制。下面右图展示了一个四足机器人的四条腿髋关节 CPG 的网络图。
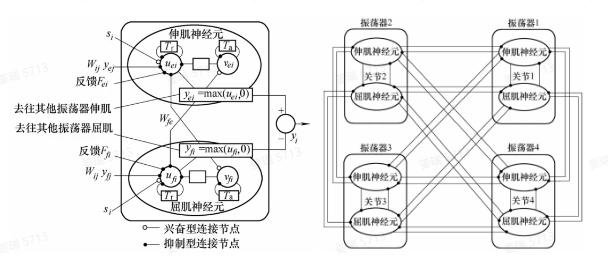
基于CPG的控制非常适合分布式实施,对像蛇形机器人之类的模块化机器人很有意义。同时,它降低了控制问题的维数,为学习和优化算法提供了良好的基础。
三、主流
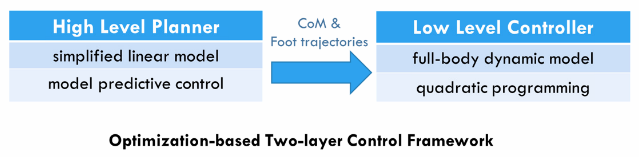
现在主流的足式机器人控制方法一般是双层结构,基于模型预观控制(MPC)的上层轨迹规划和基于动力学模型的下层全身关节力控(WBC)。它可以认为是经典的ZMP控制的升级版,计算机性能的提升让更复杂的优化问题的求解成为可能,同时高性能的力控关节也取代了ZMP时代的高刚度位控关节。这种控制架构得到了广泛的使用,并取得了很好的效果,像ETH的ANYMAL,MIT的mini-cheetah,DLR的TORO以及IHMC和CMU团队在Atlas上都采用了类似的架构。

在实际应用过程中,各个研究团队在模型的选择和具体优化目标约束的设置上各有不同,本文在这里只介绍一个最基础的方案。
和ZMP控制类似,机器人的运动可以抽象成一个单质点或单刚体来表示。下图中右上角的等式是考虑了机器人绕质心角动量的y-z平面单刚体模型。如果忽略角动量的影响并假设质心高度不变,机器人的运动可以简化成一个三维的单质点模型,如下图右下角等式。
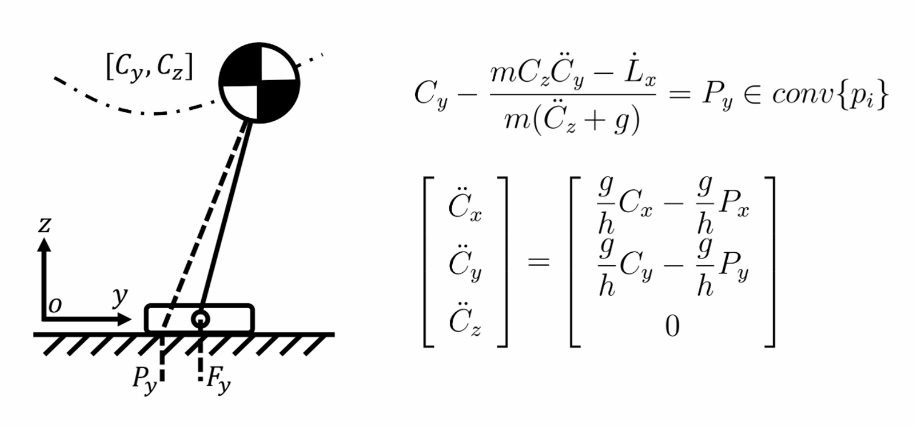
将简化模型离散化之后,我们可以将预观时间窗口内的运动构造成一个优化问题,以此来解算出最优的运动轨迹。如下图,我们期望质心跃度尽量小,保证生成的轨迹平滑,ZMP的偏离尽量小确保运动的稳定性,同时不要偏离期望速度太多。此外,生成的轨迹还需满足ZMP在支撑域内,落脚点在可达范围内等约束条件。

质心轨迹规划和ZMP控制非常类似,只是使用了优化工具,可以增加更复杂的目标和约束条件。现在的足式机器人相比十年前的稳定性能有了显著的提升,很重要的一个原因是使用了力控电机和下面要介绍的全身关节力控。相比于高刚度位控电机,力控电机通过借助模型计算的前馈力矩可以在保证轨迹跟踪精度的情况下使用小得多的反馈量,这对接触状态频繁切换,着地冲击影响显著的足式运动至关重要,大大提高了运动的稳定性和抗干扰能力。
而全身关节力控基于机器人完整的刚体动力学模型,将各个关节力矩的分配表达成一个优化问题:如下图,优化目标是减小质心和末端执行器轨迹的跟踪误差等用户需求,优化变量是关节的加速度和足底的接触力,约束包括符合动力学模型,满足关节力矩限制,符合支撑腿足底不动等物理假设,足底力满足摩擦锥要求以及ZMP在支撑域内保证脚掌不翻转等要求。优化得到的关节加速度和足底接触力再通过逆动力学就可以得到各个关节期望的前馈力矩。
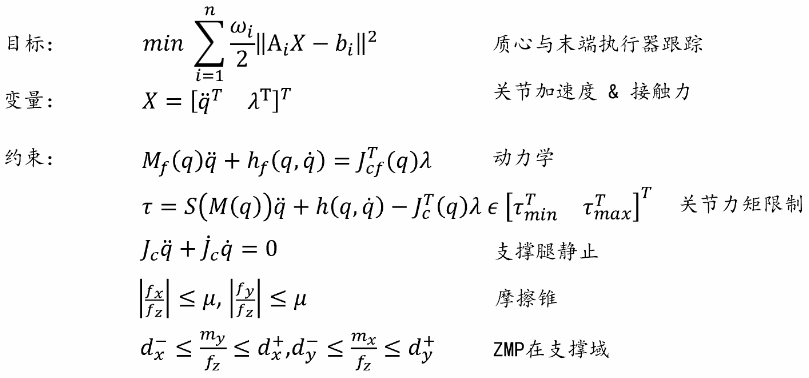
上面介绍的是一个基础方案,在实际应用中,各个研究团队会有不同的变种,比如MIT的mini-cheetah在MPC中采用考虑机身姿态的单刚体模型,同时WBC会考虑MPC中优化生成的足底力。在WBC优化变量的选取上,有的团队考虑到表达的简洁,方便加额外的优化目标和约束条件,会选择直接将关节力矩作为优化变量,或者关节加速度和关节力矩并存。
四、结语
虽然现有的足式机器人已经有很好的运动稳定性,能实现动物中常见的各种步态,但面对一些复杂的,超高机动性的动作时还是有点捉襟见肘。有研究者尝试通过非线性优化离线生成复杂的动作,然后利用全身力控来在线跟踪调整,已经取得了不少令人印象深刻的成果。如何实现非线性优化的实时在线解算,是很多研究工作者持续努力改进的方向。
最近,基于机器学习、特别是深度强化学习的控制方法在足式机器人的控制领域得到了广泛的关注,像ETH的ANYMAL团队已经在这个方向上多有建树。它所具有的学习泛化能力,让人们对将它应用于复杂动作的生成充满期待。运动控制算法的日趋完善,电机、IMU、处理器等核心器件规模化带来的低成本,催生了一批新兴的足式机器人公司,让这些以前只在实验室里的家伙频频出现在我们生活中,相信不久的将来,它们会成为新世纪的宠物,常伴我们左右。
参考文献
[1] https://www.animatornotebook.com/learn/quadrupeds-gaits
[2] Raibert M H. Legged robots that balance[M]. MIT press, 1986.
[3] Pratt J E. Virtual model control of a biped walking robot[J]. 1995.
[4] Kajita S, et al. Humanoid robotics[M]. Ohm-sha, 2005.
[5] Huang, Bo, Yufeng Yao, and Lining Sun. Quadruped robot gait control based on central pattern generator[J]. Journal of Mechanical Engineering, 2010.
[6] Ijspeert, Auke Jan, et al. From swimming to walking with a salamander robot driven by a spinal cord model[J], Science, 2007.
[7] Hutter, M., et al. Anymal-a highly mobile and dynamic quadrupedal robot[IROS], 2016.
[8] Englsberger, J., et al. Overview of the torque-controlled humanoid robot TORO[Humanoids], 2014.
[9] Koolen, T., et al. Design of a Momentum-Based Control Framework and Application to the Humanoid Robot Atlas[Humanoids], 2016.
[10] Kim, D.; Carlo, J. D.; Katz, B.; Bledt, G. & Kim, S. Highly Dynamic Quadruped Locomotion via Whole-Body Impulse Control and Model Predictive Control, 2019.
[11] Miki T, Lee J, Hwangbo J, et al. Learning robust perceptive locomotion for quadrupedal robots in the wild[J]. Science Robotics, 2022.
END


-
相关阅读:
腾讯mini项目-【指标监控服务重构】2023-08-23
Store:海量实用工具,让工作更加高效,更加轻松!
G1垃圾回收器学习笔记
面试 Python 基础八股文十问十答第七期
一文读懂苹果的差分隐私技术原理
金融领域:产业链知识图谱包括上市公司、行业和产品共3类实体,构建并形成了一个节点10w+,关系边16w的十万级别产业链图谱
c++视觉处理---图像重映射
10-Mysql内核查询成本计算实战-06
DiFi A Go-as-You-Pay Wi-Fi Access System 精读笔记(三)
【数据结构】链表
- 原文地址:https://blog.csdn.net/pengzhouzhou/article/details/125512654