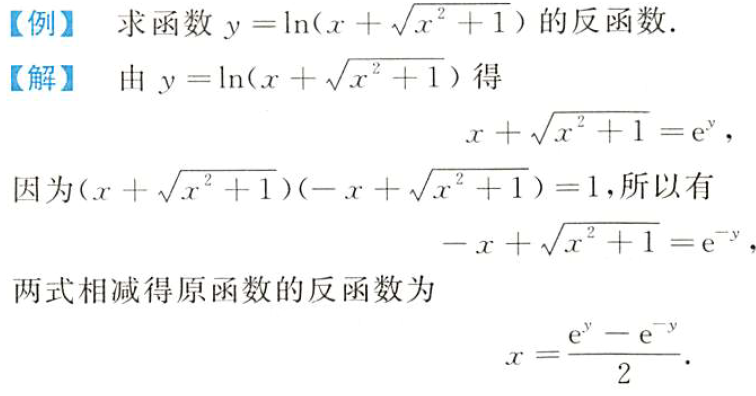-
math_数学表达式&等式方程的变形&组合操作技巧/手段积累
数学表达式&等式方程的变形&组合操作技巧/手段积累
分式
-
分子分母同时乘以&除以同一个表达式
- 分子有理化
- 分母有理化
-
分式拆分(因子重组)
方程(等式)
方程
数学中,方程(equation)可以简单的理解为含有未知数的等式,
- 即含有一个以上的未知数并结合等号的数学公式(formula)
等式
在数学的领域中,若两个数学对象在各个方面都相同,则称他们是相等的。这就定义了一个二元谓词等于,写作
x = y {\displaystyle x=y} x=y
当且仅当x和y相等。通常意义上,等于是通过两个元素间的等价关系来构造的。
将两个表达式用等于符号连起来,就构成了等式,
注意,有些时候
A = B {\displaystyle A=B} A=B
并不表示等式。例如,
T ( n ) = O ( n 2 ) {\displaystyle T(n)=O(n^{2})} T(n)=O(n2)
表示在数量级
n 2 {\displaystyle n^{2}} n2
因为这里的符号=不满足当且仅当的定义,所以它不等于等于符号;实际上,
O ( n 2 ) = T ( n ) {\displaystyle O(n^{2})=T(n)} O(n2)=T(n)
是没有意义的。请参见大O符号了解这部分内容。常见手法
-
错位相减
-
等式两边同时做相同的处理
- 1的代换(譬如
- 三角函数: 1 = s i n 2 x + c o s 2 x 1=sin^2x+cos^2x 1=sin2x+cos2x
- 幂: ( x + x 2 + 1 ) ( − x + x 2 + 1 ) = 1 (x+\sqrt{x^2+1})(-x+\sqrt{x^2+1})=1 (x+x2+1)(−x+x2+1)=1
- 同时乘方
- 同时加上某一个表达式
- 带入消元(减小变量个数)
- 等式组加减消元
- 譬如,函数的最值相关问题
- 1的代换(譬如
一般表达式处理
表达式(expression)此处是数学表达式(mathematical expression)的简称,
-
列项相消
-
譬如一部分的数列求和
-
∑
i
=
1
n
1
(
i
)
(
i
+
1
)
=
∑
i
=
1
n
1
(
i
)
−
1
(
i
+
1
)
=
∑
i
=
1
n
1
i
−
∑
i
=
1
n
1
i
+
1
=
(
1
1
+
∑
i
=
2
n
1
i
)
−
(
∑
i
=
2
n
1
i
+
1
n
+
1
)
=
1
−
1
1
+
n
令
:
{
f
(
i
)
=
1
i
;
则
g
(
i
)
=
f
(
i
+
1
)
‾
=
1
i
+
1
,
可
见
是
一
个
(
离
散
)
函
数
的
向
左
偏
移
1
\sum\limits_{i=1}^n{\frac{1}{(i)(i+1)}} =\sum\limits_{i=1}^n{\frac{1}{(i)}-\frac{1}{(i+1)}} =\sum\limits_{i=1}^n{\frac{1}{i}} -\sum\limits_{i=1}^{n}\frac{1}{i+1} \\=(\frac{1}{1}+\sum\limits_{i=2}^{n}{\frac{1}{i}}) -(\sum\limits_{i=2}^{n}\frac{1}{i}+\frac{1}{n+1}) \\=1-\frac{1}{1+n} \\ 令:i=1∑n(i)(i+1)1=i=1∑n(i)1−(i+1)1=i=1∑ni1−i=1∑ni+11=(11+i=2∑ni1)−(i=2∑ni1+n+11)=1−1+n1令:{f(i)=i1;则g(i)=f(i+1)=i+11,可见是一个(离散)函数的向左偏移1
-
∑
i
=
1
n
1
(
i
)
(
i
+
1
)
=
∑
i
=
1
n
1
(
i
)
−
1
(
i
+
1
)
=
∑
i
=
1
n
1
i
−
∑
i
=
1
n
1
i
+
1
=
(
1
1
+
∑
i
=
2
n
1
i
)
−
(
∑
i
=
2
n
1
i
+
1
n
+
1
)
=
1
−
1
1
+
n
令
:
{
f
(
i
)
=
1
i
;
则
g
(
i
)
=
f
(
i
+
1
)
‾
=
1
i
+
1
,
可
见
是
一
个
(
离
散
)
函
数
的
向
左
偏
移
1
\sum\limits_{i=1}^n{\frac{1}{(i)(i+1)}} =\sum\limits_{i=1}^n{\frac{1}{(i)}-\frac{1}{(i+1)}} =\sum\limits_{i=1}^n{\frac{1}{i}} -\sum\limits_{i=1}^{n}\frac{1}{i+1} \\=(\frac{1}{1}+\sum\limits_{i=2}^{n}{\frac{1}{i}}) -(\sum\limits_{i=2}^{n}\frac{1}{i}+\frac{1}{n+1}) \\=1-\frac{1}{1+n} \\ 令:
-
-
对数&指数的转化
-
换元法
-
配凑法
-
加上一个表达式再减去相同大小的表达式
-
例如,分离常数:(可以起到集中变量x的效果)
- f ( x ) = 2 x − 1 x + 1 = 2 x − 1 + 2 − 2 1 2 ( 2 x + 2 ) = 2 x + 2 − 3 x + 1 = 2 + − 3 x + 1 f(x)=\frac{2x-1}{x+1}=\frac{2x-1+2-2}{\frac{1}{2}(2x+2)} =\frac{2x+2-3}{x+1}=2+\frac{-3}{x+1} f(x)=x+12x−1=21(2x+2)2x−1+2−2=x+12x+2−3=2+x+1−3
-
再比如导函数求导法则种的乘法求导法则的推导/证明:
- f ( x ) = u ( x ) v ( x ) f ′ ( x ) = lim Δ x → 0 f ( x + Δ x ) − f ( x ) Δ x = lim Δ x → 0 u ( x + Δ x ) v ( x + Δ x ) − u ( x ) v ( x ) Δ x = lim Δ x → 0 u ( x + Δ x ) v ( x + Δ x ) − u ( x ) v ( x ) + u ( x ) v ( x + Δ x ) − u ( x ) v ( x + Δ x ) Δ x 配 凑 & 组 合 = lim Δ x → 0 [ ( u ( x + Δ x ) − u ( x ) ) v ( x + Δ x ) ] + [ u ( x ) ( v ( x + Δ x ) − v ( x ) ) ] Δ x = lim Δ x → 0 { ( u ( x + Δ x ) − u ( x ) ) Δ x ⋅ v ( x + Δ x ) + u ( x ) ⋅ ( v ( x + Δ x ) − v ( x ) ) Δ x } = lim Δ x → 0 ( u ( x + Δ x ) − u ( x ) ) Δ x ⋅ v ( x + Δ x ) + lim Δ x → 0 u ( x ) ⋅ ( v ( x + Δ x ) − v ( x ) ) Δ x = lim Δ x → 0 ( u ( x + Δ x ) − u ( x ) ) Δ x lim Δ x → 0 v ( x + Δ x ) + lim Δ x → 0 u ( x ) lim Δ x → 0 ( v ( x + Δ x ) − v ( x ) ) Δ x = u ′ ( x ) v ( x ) + u ( x ) v ′ ( x ) f(x)=u(x)v(x) \\ f'(x)=\lim_{\Delta x\rightarrow 0} {\frac{f(x+\Delta x)-f(x)}{\Delta x}} \\=\lim_{\Delta x\rightarrow 0} \frac{{u(x+\Delta x)v(x+\Delta x)-u(x)v(x)}}{\Delta x} \\=\lim_{\Delta x\rightarrow 0} \frac{{u(x+\Delta x)v(x+\Delta x)-u(x)v(x) +u(x)v(x+\Delta x)-u(x)v(x+\Delta x)}} {\Delta x} \\配凑\&组合 \\ =\lim_{\Delta x\rightarrow 0} \frac{[(u(x+\Delta x)-u(x))v(x+\Delta x)] +[u(x)(v(x+\Delta x)-v(x))]} {\Delta x} \\=\lim\limits{\Delta x\rightarrow 0} \left \{ {\frac{(u(x+\Delta x)-u(x))}{\Delta x}\cdot v(x+\Delta x) +u(x)\cdot \frac{(v(x+\Delta x)-v(x))}{\Delta x}} \right \} \\=\lim_{\Delta x\rightarrow0} {\frac{(u(x+\Delta x)-u(x))}{\Delta x}\cdot v(x+\Delta x)} +\lim_{\Delta x\rightarrow0}u(x)\cdot \frac{(v(x+\Delta x)-v(x))}{\Delta x} \\=\lim_{\Delta x\rightarrow0} {\frac{(u(x+\Delta x)-u(x))}{\Delta x}\lim_{\Delta x\rightarrow0} v(x+\Delta x)} \\ +\lim_{\Delta x\rightarrow0}u(x)\lim_{\Delta x\rightarrow0} \frac{(v(x+\Delta x)-v(x))}{\Delta x} \\=u'(x)v(x)+u(x)v'(x) f(x)=u(x)v(x)f′(x)=Δx→0limΔxf(x+Δx)−f(x)=Δx→0limΔxu(x+Δx)v(x+Δx)−u(x)v(x)=Δx→0limΔxu(x+Δx)v(x+Δx)−u(x)v(x)+u(x)v(x+Δx)−u(x)v(x+Δx)配凑&组合=Δx→0limΔx[(u(x+Δx)−u(x))v(x+Δx)]+[u(x)(v(x+Δx)−v(x))]=limΔx→0{Δx(u(x+Δx)−u(x))⋅v(x+Δx)+u(x)⋅Δx(v(x+Δx)−v(x))}=Δx→0limΔx(u(x+Δx)−u(x))⋅v(x+Δx)+Δx→0limu(x)⋅Δx(v(x+Δx)−v(x))=Δx→0limΔx(u(x+Δx)−u(x))Δx→0limv(x+Δx)+Δx→0limu(x)Δx→0limΔx(v(x+Δx)−v(x))=u′(x)v(x)+u(x)v′(x)
-
-
拆项相消
-
方程组成组处理(经常是相加/减)法
-
很多和1有关
-
直观的例子
- 这里的
元可能是指复杂的式子(作为整体)
-
-
相关阅读:
2024初三集训模拟测试1
优维低代码实践:图片和搜索
TCP三次握手四次挥手
2023牛客OI赛前集训营-提高组(第二场)B.出租
【排序算法】图解直接插入排序(图解堪比Debug显示每次循环结果)
北京筑龙:快消品行业如何迈入采购数字化快车道?
ES相关面试问题整理
部署基于docker和cri-dockerd的Kubernetes v1.25.3
SegNet & DeconvNet——论文阅读
通过leangoo建立你的清单管理系统
- 原文地址:https://blog.csdn.net/xuchaoxin1375/article/details/125514117