2022/6/28学习总结

 一、3. 无重复字符的最长子串 - 力扣（LeetCode）

 题目描述：

给定一个字符串 s ，请你找出其中不含有重复字符的 最长子串 的长度。

示例 1:

输入: s = "abcabcbb"
输出: 3 
解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。
示例 2:

输入: s = "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b"，所以其长度为 1。
示例 3:

输入: s = "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke"，所以其长度为 3。
     请注意，你的答案必须是 子串 的长度，"pwke" 是一个子序列，不是子串。
 

提示：

0 <= s.length <= 5 * 104
s 由英文字母、数字、符号和空格组成

 思路：

记录字符在遍历的字符串里面最后出现的位置，通过位置判断是否已经出现在该字符串中。后面的解题思路在代码中有详细解释。

代码实现：

class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        int start=0,l=0,max=0,a[128];
        for(int i=0;i<128;i++)//记录在遍历到的位置之前该字母最后出现的位置
        {
            a[i]=-1;//初始化，初始化的数字，只能是小于0的数字
        }
        for(int i=0;i<s.length();i++)
        {
            if(a[s[i]]>=start)//前面已经出现该字符
            {
                if(l>max)//更新最长不重复子串长度
                {
                    max=l;
                }
                l=i-a[s[i]];//更新新的子串的有效长度
                start=a[s[i]]+1;//更新新的子串在母串中的起始位置
                a[s[i]]=i;//该字母出现过，更新该字母在遍历到的位置之前最后出现的位置
            }
            else//未出现该字符
            {
                a[s[i]]=i;//该字母未出现过，记录该字母在遍历到的位置之前最后出现的位置
                l++;//长度加一
            }
        }
        if(l>max)//有可能遍历到了最后，最长不重复子串才出现，那么max没有更新，所以在这里进行更新
        {
            max=l;
        }
        return max;
    }
};

二、146. LRU 缓存 - 力扣（LeetCode）

题目描述：

 请你设计并实现一个满足  LRU (最近最少使用) 缓存 约束的数据结构。
实现 LRUCache 类：
LRUCache(int capacity) 以 正整数 作为容量 capacity 初始化 LRU 缓存
int get(int key) 如果关键字 key 存在于缓存中，则返回关键字的值，否则返回 -1 。
void put(int key, int value) 如果关键字 key 已经存在，则变更其数据值 value ；如果不存在，则向缓存中插入该组 key-value 。如果插入操作导致关键字数量超过 capacity ，则应该 逐出 最久未使用的关键字。
注意：函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。

示例：

输入
["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
输出
[null, null, null, 1, null, -1, null, -1, 3, 4]

解释
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // 缓存是 {1=1}
lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}
lRUCache.get(1);    // 返回 1
lRUCache.put(3, 3); // 该操作会使得关键字 2 作废，缓存是 {1=1, 3=3}
lRUCache.get(2);    // 返回 -1 (未找到)
lRUCache.put(4, 4); // 该操作会使得关键字 1 作废，缓存是 {4=4, 3=3}
lRUCache.get(1);    // 返回 -1 (未找到)
lRUCache.get(3);    // 返回 3
lRUCache.get(4);    // 返回 4
 

提示：

1 <= capacity <= 3000
0 <= key <= 10000
0 <= value <= 105
最多调用 2 * 105 次 get 和 put

思路：

双向链表+哈希表。因为有时候，要移动的结点位于链表的中间位置，移动的话，得进行删除结点和增加结点这两步，删除该结点的话，得同时找到该节点的前驱结点和后继结点，所以用双向链表方便。然后，get()函数和put()函数，都要去查看结点是否存在，同时时间复杂度要为O(1)，所以得用哈希表。

代码实现：

 class LRUCache {
    struct LinkNode {//结点结构
        int value;
        int key;
        LinkNode* prior;
        LinkNode* next;
    };
 
    LinkNode* head=new LinkNode;//头结点，方便结点的删除和增加
    LinkNode* tail=new LinkNode;//尾结点
    map<int,LinkNode*> mp;//map，方便查找key和value，使得函数 get 和 put 必须以 O(1) 的平均时间复杂度运行
    int c,sum=0;//缓存容量，已缓存的容量
 
public:
    LRUCache(int capacity) {
        c = capacity;//得到缓存容量
        head->next = tail;//空的双向链表
        tail->prior = head;
    }
    
    int get(int key) {
        if(mp.count(key))
        {
            remove(mp[key]);//刚刚使用过，所以把这个结点往前移动，先删除结点
            add(head,mp[key]);//再增加结点
            return mp[key]->value;//存在
        }
        return -1;//不存在
    }
    
    void put(int key, int value) {
        if(mp.count(key))//key值存在
        {
            remove(mp[key]);//刚刚使用过，所以把这个结点往前移动，先删除结点
            add(head,mp[key]);//增加结点
            mp[key]->value=value;//因为key值存在，但value值可能和已经存储的value值不同，所以以函数里面的为主
            return;
        }
        LinkNode* node=new LinkNode;//不存在，增加结点
        node->key=key;
        node->value=value;
        add(head,node);
        sum++;
        mp[key]=node;
        if(sum>c)
        {
            LinkNode* p=tail->prior;
            remove(tail->prior);//删除最后一个结点，也就是最久未使用的结点
            sum--;
            mp.erase(p->key);
        }
        return;
    }
 
    void remove(LinkNode* node)//删除结点node
    {
        node->next->prior=node->prior;
        node->prior->next=node->next;
    }
 
    void add(LinkNode* node,LinkNode* p)//在结点node后面添加结点p
    {
        p->next=node->next;
        p->prior=node;
        node->next->prior=p;
        node->next=p;
    }
};
 
/**
 * Your LRUCache object will be instantiated and called as such:
 * LRUCache* obj = new LRUCache(capacity);
 * int param_1 = obj->get(key);
 * obj->put(key,value);
 */

三、215. 数组中的第K个最大元素 - 力扣（LeetCode）

题目描述 

给定整数数组 nums 和整数 k，请返回数组中第 k 个最大的元素。

请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。

示例 1:

输入: [3,2,1,5,6,4] 和 k = 2
输出: 5
示例 2:

输入: [3,2,3,1,2,4,5,5,6] 和 k = 4
输出: 4
 

提示：

1 <= k <= nums.length <= 104
-104 <= nums[i] <= 104

思路：

用排序算法（这里采用的快排），然后拿取倒数第k个元素即可。

代码实现：

class Solution {
public:
    void quickSort(vector<int>& nums, int l, int r)
    {
        if(l>r)
        {
            return;
        }
        int left=l;
        int right=r;
        int sign=nums[left];
        while(left<right)
        {
            while(left<right&&nums[right]>=sign)
            {
                right--;
            }
            if(nums[right]<sign)
            {
                nums[left]=nums[right];
            }
            while(left<right&&nums[left]<=sign)
            {
                left++;
            }
            if(nums[left]>sign)
            {
                nums[right]=nums[left];
            }
            if(left>=right)
            {
                nums[right]=sign;
            }
        }
        quickSort(nums,l,right-1);
        quickSort(nums,left+1,r);
    }
    int findKthLargest(vector<int>& nums, int k) {
        quickSort(nums,0,nums.size()-1);
        return nums[nums.size()-k];
    }
};

四、P1044 [NOIP2003 普及组] 栈 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

题目背景

栈是计算机中经典的数据结构，简单的说，栈就是限制在一端进行插入删除操作的线性表。

栈有两种最重要的操作，即 pop（从栈顶弹出一个元素）和 push（将一个元素进栈）。

栈的重要性不言自明，任何一门数据结构的课程都会介绍栈。宁宁同学在复习栈的基本概念时，想到了一个书上没有讲过的问题，而他自己无法给出答案，所以需要你的帮忙。

题目描述

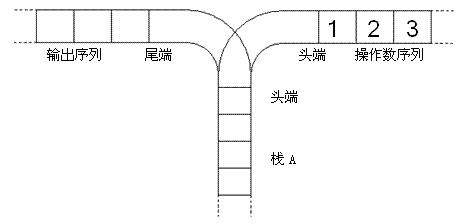
宁宁考虑的是这样一个问题：一个操作数序列，1,2,…,n（图示为 1 到 3 的情况），栈 A 的深度大于 n。

现在可以进行两种操作，

1. 将一个数，从操作数序列的头端移到栈的头端（对应数据结构栈的 push 操作）
2. 将一个数，从栈的头端移到输出序列的尾端（对应数据结构栈的 pop 操作）

使用这两种操作，由一个操作数序列就可以得到一系列的输出序列，下图所示为由 1 2 3 生成序列 2 3 1 的过程。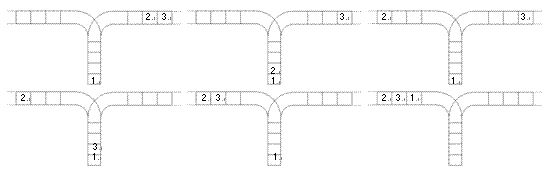

（原始状态如上图所示）

你的程序将对给定的 n，计算并输出由操作数序列 1,2,…,n 经过操作可能得到的输出序列的总数。

输入格式

输入文件只含一个整数 n（1≤n≤18）。

输出格式

输出文件只有一行，即可能输出序列的总数目。

输入输出样例

输入 #1复制

3

输出 #1复制

5

说明/提示

【题目来源】

NOIP 2003 普及组第三题

思路：递归法。

栈可以进行入栈和出栈的操作。后面思路在代码里面解释了。

代码实现：

#include<bits/stdc++.h>
using namespace std;
int main()
{
    int n;
    scanf("%d",&n);
    int a[20][20];//行数表示未进栈的数的个数，列数表示栈内的数的个数
    for(int i=0;i<20;i++)
    {
        a[0][i]=1;//如果元素全部进栈，那元素只有出栈，而且只有一种出栈序列
    }
    for(int i=1;i<20;i++)
    {
        for(int j=0;j<20;j++)
        {
            if(j==0)//栈内元素为0个时，可以进行的操作只有入栈
            {
                a[i][j]=a[i-1][j+1];
            }
            else
            {
                a[i][j]=a[i-1][j+1]+a[i][j-1];//栈内元素个数不为0时，可以进行入栈和出栈
            }
        }
    }
    printf("%d",a[n][0]);//出栈序列的种数，即未入栈元素个数为n，栈内元素为0个时
}

五、P1449 后缀表达式 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

题目描述

所谓后缀表达式是指这样的一个表达式：式中不再引用括号，运算符号放在两个运算对象之后，所有计算按运算符号出现的顺序，严格地由左而右新进行（不用考虑运算符的优先级）。

如：3*(5–2)+7对应的后缀表达式为：3．5．2．-*7．+@。’@’为表达式的结束符号。‘.’为操作数的结束符号。

输入格式

输入：后缀表达式

输出格式

输出：表达式的值

输入输出样例

输入 

3.5.2.-*7.+@

输出 

16

说明/提示

字符串长度，1000内。

 

思路：该题不需要考虑到'+' '-'为单目运算符的情况。

不需要考虑上面的那种情况后，这题就很简单了。

操作数的拿取要注意。每个操作数后面都有一个 '.'，这就方便了我们拿取操作数。我们拿取的操作数应该是遇到的第一个数字字符到 '.'之前的所以数字字符组成的整型数字，然后入栈。

然后对于操作符，该题没有考虑单目运算符的情况。所以每次拿取操作数都是两个，然后再将运算结果入栈，最后栈底的元素即为后缀表达式的运算结果。

代码实现：

#include<bits/stdc++.h>
using namespace std;
int main()
{
    char s[1001];//输入的字符串
    int c[1001];//存放操作数
    int i=0,j=0;
    while((s[i]=getchar())!='@')//输入字符串
    {
        i++;
    }
    s[i]='\0';
    for(i=0; i<strlen(s); i++)
    {
        if(s[i]>='0'&&s[i]<='9')//拿取操作数，入栈
        {
            int m=1,x;
            x=s[i]-'0';
            i++;
            while(s[i]!='.')//拿取遇到的第一个数字字符，到'.'之前的所有字符组成的数字
            {
                x=x*10+s[i]-'0';
                m++;
                i++;
            }
            c[j]=x;//入栈
            j++;
        }
        if(s[i]=='-')//都是双目运算符
        {
            int x=c[j-2]-c[j-1];
            j=j-2;
            c[j]=x;//将运算后的结果入栈
            j++;
        }
        if(s[i]=='+')
        {
            int x=c[j-2]+c[j-1];
            j=j-2;
            c[j]=x;
            j++;
        }
        if(s[i]=='*')
        {
            int x=c[j-2]*c[j-1];
            j=j-2;
            c[j]=x;
            j++;
        }
        if(s[i]=='/')
        {
            int x=c[j-2]/c[j-1];
            j=j-2;
            c[j]=x;
            j++;
        }
    }
    printf("%d",c[0]);//栈底元素即为后缀表达式的运算结果
    return 0;
}