LeetCode高频题300. 最长递增子序列

提示：本题是系列LeetCode的150道高频题，你未来遇到的互联网大厂的笔试和面试考题，基本都是从这上面改编而来的题目
互联网大厂们在公司养了一大批ACM竞赛的大佬们，吃完饭就是设计考题，然后去考应聘人员，你要做的就是学基础树结构与算法，然后打通任督二脉，以应对波云诡谲的大厂笔试面试题！
你要是不扎实学习数据结构与算法，好好动手手撕代码，锻炼解题能力，你可能会在笔试面试过程中，连题目都看不懂！比如华为，字节啥的，足够让你读不懂题

这是一个非常困难，但是又极其经典的动态规划，我最开始也没学懂，这是我第五次复习，终于看懂了
也想清楚了其中的原理，因此，我透彻地总结一下！

基础知识：
【1】二分法查找有序数组arr中，大于等于k的最左侧、最右侧的位置

---

文章目录

• LeetCode高频题300. 最长递增子序列
• • @[TOC](文章目录)
• 题目
• 一、审题
• 涉及子序列或者子数组，就是彻底的考虑以i开头或者i结尾的状况！
• 暴力解怎么搞？
• 前奏知识，我们说了多次：二分法寻找arr中>=k的最左的位置index
• 笔试面试最优解：额外空间换时间，利用ends来加速求解
• • 拿这个ends干嘛呢？？？
  • 再举例ends怎么填
• 总结

题目

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

子序列 是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。
例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/longest-increasing-subsequence
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

---

一、审题

示例 1：

输入：nums = [10,9,2,5,3,7,101,18]
输出：4
解释：最长递增子序列是 [2,3,7,101]，因此长度为 4 。
示例 2：

输入：nums = [0,1,0,3,2,3]
输出：4
0 1 2 3
示例 3：

输入：nums = [7,7,7,7,7,7,7]
输出：1
7
严格递增哦！

提示：

1 <= nums.length <= 2500
-104 <= nums[i] <= 104

---

涉及子序列或者子数组，就是彻底的考虑以i开头或者i结尾的状况！

讲了无数次了这个知识点！

本题，子序列，老样子，考虑必须以i结尾的子序列的最大长度是多少？将这个结果放入dp表格中存好。
dp[i]就是代表必须以i结尾的子序列的最大长度

结果就是看dp[i]哪个格子最大。

比如arr=3 1 4 2 3
显然

最终max=3

不过这个题和普通动态规划有点区别

这是一个非常困难，但是又极其经典的动态规划，我最开始也没学懂，这是我第五次复习，终于看懂了
也想清楚了其中的原理，因此，我透彻地总结一下！

最长递增子序列的经典应用：
俄罗斯套娃问题，信封嵌套问题，曲线上连续递增的点个数问题，都是源自本题的算法原型。

暴力解怎么搞？

来到i，往左看看，有多少元素是持续递减的，i就是严格递增子序列的结尾
统计这个长度，更新给max

最后max就是结果

相当于考虑每一个i做结尾情况下，哪个递增子序列最长

外围N个调度
内部每次需要N次对比，向左对比
总的复杂度o(n^2)

代码就不撸了，没趣

        public int lengthOfLIS(int[] nums) {
            if (nums == null || nums.length == 0) return 0;

            int N = nums.length;
            int[] dp = new int[N];
            dp[0] = 1;//一个元素没啥可说的

            int max = 1;
            for (int i = 1; i < N; i++) {
                dp[i] = 1;//最次也就1
                for (int j = 0; j < i; j++) {
                    if (nums[i] > nums[j]) dp[i] = Math.max(dp[i], dp[j] + 1);
                }
                //每个dp[i]取最值
                max = Math.max(max, dp[i]);
            }

            return max;
        }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

直接看下面最优解，非常经典，要想尽一切办法理解透，然后记住它！
据说这个算法原型，比bfprt出现在互联网大厂面试中的频率还高！

前奏知识，我们说了多次：二分法寻找arr中>=k的最左的位置index

【1】二分法查找有序数组arr中，大于等于k的最左侧、最右侧的位置

        //这里头很重要的是，有序数组，找到arr中大于等于target的最左的那个位置
        public static int leftest(int[] nums, int L, int R, int target){
            //从L--R中找
            while (L <= R){
                int mid = L + ((R - L) >> 1);
                if (target <= nums[mid]) R = mid - 1;//还得继续往左，逼近最左那个数——————这里就是重点
                else L = mid + 1;//target > nums[mid]，显然target太大，还得继续往右找
            }
            return L;//最后的L 就是最左的位置
        }
1
2
3
4
5
6
7
8
9
10

逼近最左那个数——————这里就是重点

---

笔试面试最优解：额外空间换时间，利用ends来加速求解

情况是这样的，我们希望通过一个数组来加速这个算法过程
挺难理解，也不难理解

这个额外数组叫ends，它干嘛的，ends[i]是啥意思呢？？？
ends[i]表示arr中严格递增子序列的长度为i+1的所有子序列中，最小的那个结尾
ends[i]表示arr中严格递增子序列的长度为i+1的所有子序列中，最小的那个结尾
ends[i]表示arr中严格递增子序列的长度为i+1的所有子序列中，最小的那个结尾

好好理解这句话

比如：arr=3 2 4 5 1 2 3 4
虽然，3、2、1都能独立成一个长度为1的严格递增子序列，但是最小的那个结尾，可是1，所以ends[0]=1

为什么要这么记录，就是为了有一个非常非常小的开头，然后我们在这个开头上，尽量添加间隔小的下一个数
比如ends[0]=1,你想整一个严格递增的子序列，我希望下一个来的的数是2，这间隔就很小，这样我能拉更长的子序列，懂不？
我更喜欢出现连续的间隔小的3 4 5 6 7，这样我能拉超级超级长，最长不会超过N个

因此ends长度最大也就是N，不会超过N

你看看长度为2的最小那个结尾应该是谁呢？【看下图粉色2个组合的子序列】

自然所有长度为2的递增子序列，最小的那个结尾是2,ends[1]=2

递增子序列为3呢？ends[2]=3

递增子序列长度为4的最小结尾呢？ends[3]=4

基本已经完结了，你看看ends实际上就4长度，没有到N

但是ends[i]记录的就是arr中长度为i+1的递增子序列最小的那个结尾。

拿这个ends干嘛呢？？？

我们来到arr的i位置，[i]是不是可能会成为ends某个位置的数呢？
比如上图中的1，应该去更新ends[0]
上图中4，应该去更新ends[3]
很有可能[i]会去更新ends某个位置的数，就看[i]会成为哪个子序列的结尾了

遇到[i]，比如上面的4，我**当然希望它直接跟在ends屁股，新增ends，这样长度变成了，我得到更大的max，**你说是吧？？

但巧了你遇到的是1，那就尴尬了，它只能成为ends[0]，也就是说你得确定你[i]应该去更新谁？
那你需要找到ends已有的所有结尾中，那个>=[i]的最左边那个位置index
你需要找到ends已有的所有结尾中，那个>=[i]的最左边那个位置index
你需要找到ends已有的所有结尾中，那个>=[i]的最左边那个位置index

这句话又要彻彻底底理解透，也很好理解的
为啥呢？
其实是这样的，我希望[i]直接接ends的屁股，扩展ends长度
但是我要看[i]有没有这个本事大于ends的末尾位置了，有可能[i]压根就小于ends后面的结尾，那你无法严格递增了呀对吧？

故，我需要找到ends已有的所有结尾中，那个>=[i]的最左边那个位置index
[i]恰好能替换ends[index]，

这样的话，既能保证[i]>ends[index-1]，做严格递增的那个，且替换ends[index]成为长度为i+1的那个子序列的最小结尾！！

比如：还是上面这个例子，我们i来到arr的6位置，[i]=4，我们已经有了ends[0–2]
我们要在ends中找那个index位置，ends[index]>=[i]的最左的那个位置

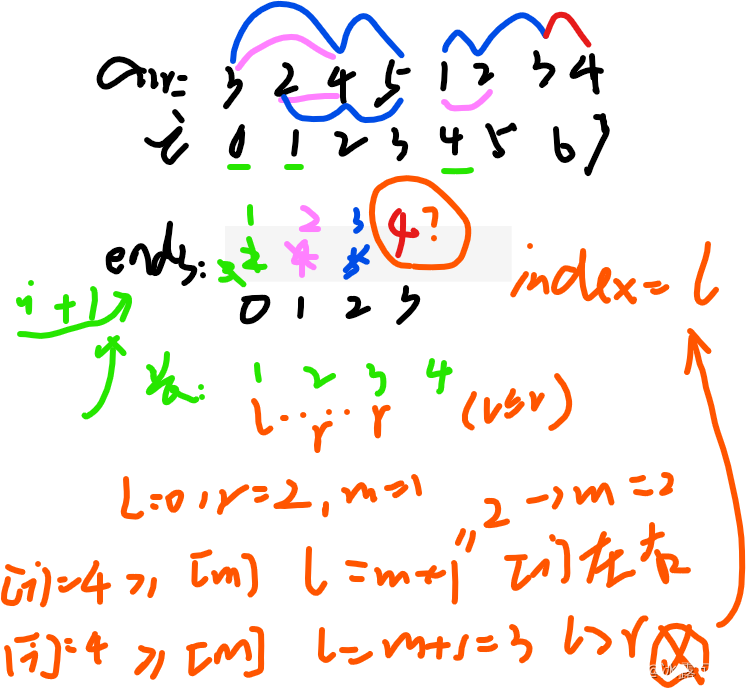
自然l=0，r=2，mid=1，去二分查找看看那个>=[i]的位置在哪？
这个知识我们见过很多遍了

俩条件
（1）如果ends[mid]<[i]，说明[i]在ends右边，下次l=mid+1=2
（2）如果ends[mid]>=[i]，说明[i]应该在ends左边，我们要找最左的位置，让下次r=mid-1，使劲往左逼近，找到那个ends[index]>=[i]的最左的index

不巧，走了（1）条件，下次l=2
mid=2
此时ends[mid]=3<[i]，因此还是走（1），下次l=mid+1=3，此刻l>r，停止寻找
此刻的l就是那个ends中>=[i]的最左的位置了，
因此ends[l]=ends[3]=[i]=4，将4放入ends
说明长度为i+1=4的子序列，以4作为最小结尾，被更新到ends中
记录此时dp[6]=l+1
更新max=dp[6]
这个寻找并更新ends[index]的复杂度，二分法，自然是o(log(n))

如果外围N个位置都这么找一遍，更新给ends，那不就是o(nlog(n))复杂度嘛？？

可不就是比暴力解好？暴力o(n^2)哦！

这就是为啥我们要用ends加速的原理！！

再举例ends怎么填

最开始来到arr的i=0位置，ends没有，直接就填ends[0]=3，更新dp[0]=1，更新max=1
来到arr的i=1位置，ends已经有1个数了，寻找ends中>=[i]=2的最左的位置，3>=2，所以ends中index=0位置的3要被[i]=2替换，2才是长度为1的递增子序列的最小的那个结尾，更新dp[1]=1，更新max=1
来到arr的i=2位置，ends已经有1个数了，寻找ends中>=[i]=4的最左的位置，没有，利用二分法找不到，最后l=1了都没有，所以ends[l]=[i]=4，长度为2的递增子序列最小结尾是4，放好ends，，更新dp[2]=2，更新max=2

来到arr的i=3位置，ends已经有2个数了，寻找ends中>=[i]=5的最左的位置，没有，利用二分法找不到，最后l=2了都没有，所以ends[l]=[i]=5，长度为3的递增子序列最小结尾是5，放好ends，，更新dp[3]=5，更新max=3
来到arr的i=4位置，ends已经有3个数了，寻找ends中>=[i]=1的最左的位置，
令l=0，r=2，二分查找，发现ends中的index=0位置的2其实是>=1的最左的位置，所以ends[l=0]=[i]=1，长度为1的递增子序列最小结尾是1，放好ends，更新dp[4]=1，更新max=3不变哦
来到arr的i=5位置，ends已经有3个数了，寻找ends中>=[i]=3的最左的位置，
令l=0，r=2，二分查找，发现ends中的index=1位置的4其实是>=3的最左的位置，所以ends[l=1]=[i]=3，长度为2的递增子序列最小结尾是3，放好ends，更新dp[5]=2，更新max=3不变哦

注意，中途r=right = Math.max(right, l);
因为每次二分查找，很可能l超过了上次的right，新增了个长度，l就是最大值，
就像最开始出现5那，l=2，实际上比上次r=1要大，下次r=right=2哦！

如何?
这个填写ends的过程，是不是很清晰？
中途更新dp[i]即可，把max更新好就是我们要的结果

其实ends干的就是将见过的子序列为固定长度的最小结尾更新好
方便下次后面来更大的元素，直接填ends屁股，这样递增子序列真的就变长了
而且我只需要log(n)速度就能找到index位置【ends中>=[i]的最左那个位置】
ends越小，越有利于我后续递增更多长度！

这个方法非常非常巧妙

因此，我们手撕一下上面这个求最长递增子序列的长度的代码把！！！
如果上面的过程没有理解，你一定要自己画画例子，然后结合我下面的代码，好生理解！反复思考，书读百遍其义自见，就是这意思！

        //复习：
        //前面几遍我是没搞懂的，今天终于透彻理解了
        public int lengthOfLISReview(int[] nums) {
            if (nums == null || nums.length == 0) return 0;
            if (nums.length == 1) return 1;

            int N = nums.length;

            //每个i位置填写ends，dp[i]，更新max
            //中途二分查找ends中>=[i]的最左那个位置，就是最小的结尾
            //dp[i]就是代表必须以i结尾的子序列的最大长度
            int[] dp= new int[N];//其实要不要dp[i]是无所谓的
            int[] ends = new int[N];//这个ends可能并不一定会到N长度，大概率不会的
            int max = 1;//最次都是1长度
            //注意，最开始ends[0]就是1长度，必然是arr[0]
            ends[0] = nums[0];//否则默认的这个0，就炸了

            int l = 0;
            int r = 0;//注意这个right可能会变大
            int right = 0;//待会用这个right记录真的ends的最大长度，lr可能都在二分法时变化，我们只要真的right
            int m = 0;
            for (int i = 0; i < N; i++) {//每个i来了，都要找ends中>=[i]的最左那个位置，就是最小的结尾
                l = 0;//每次二分查找都是0--r范围哦，别忘了
                r = right;//这个right是真的ends的右边界
                while (l <= r){
                    //俩条件
                    m = l + ((r - l) >> 1);//中点
                    //（1）如果nums[i] > ends[m]，说明[i]在ends右边，下次l=mid+1=2
                    if (nums[i] > ends[m]) l = m + 1;
                    //（2）如果[i]<=ends[mid]，说明[i]应该在ends左边，我们要找最左的位置，让下次r=mid-1，
                    // 使劲往左逼近，找到那个ends[index]>=[i]的最左的index
                    else r = m - 1;
                }
                //一旦l>r，说明此时l=index，找到了
                ends[l] = nums[i];//更新这个最小的结尾
                //l+1就是此时的递增子序列的长度
                dp[i] = l + 1;
                max = Math.max(max, dp[i]);//dp就一个变量也行的
                right = Math.max(right, l);//很可能l超过了上次的r，新增了个长度，l就是最大值
            }

            return max;
        }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

测试一把：

    public static void test(){
        int[] arr = {3,2,4,5,1,3};
        Solution solution = new Solution();
        System.out.println(solution.lengthOfLIS(arr));
        System.out.println(solution.longestUpSubSequenceLen2(arr));
        System.out.println(solution.lengthOfLISReview(arr));
    }

    public static void main(String[] args) {
        test();
    }
1
2
3
4
5
6
7
8
9
10
11

暴力解也测试了，问题不大

3
3
3
1
2
3

优化解也OK

LeetCode测试:


厉害吧？
这个end是的强大，就是最牛的
right标记了right的真实最右边界
每次l=0，r=right，从ends中找>=[i]的最左那个位置，更新长度为l+1的ends[l]作为最小结尾
每次i搞完，我们就知道必须以i结尾的子序列长度是多少？更新给max

懂？
如何使用到俄罗斯套娃上，咱们下文继续说

---

总结

提示：重要经验：

1）最长递增子序列问题，非常非常有用，解决最长递增子序列的最大长度这个问题，以i结尾的子序列，长度是多少呢？用ends数组加速
2）ends数组记录长度是l+1的递增子序列最小结尾是谁？我们希望放小点的结尾，这样后续来稍微大点的数，能接ends屁股作为递增子序列。
3）笔试求AC，可以不考虑空间复杂度，但是面试既要考虑时间复杂度最优，也要考虑空间复杂度最优。