解答算法题的时候，我们经常要借助一些数据结构（哈希表，栈等）或者java.util.*包中的 API （数组排序等）来完成算法题的逻辑。当然，不是所有的时候都能想到某种题型应该使用哪种数据结构，所以在这里总结一下经常能用到的数据结构，以及比较典型的题型。

当然，总结的规模肯定是和刷过的题成正比的，所以本文会尽可能的归类整理这些数据结构和API的使用场景。

1、数组排序

一般对于数组结构的算法题，很多题目需要对数组重新排序之后，才能更好的完成解答逻辑。这时就需要使用Arrays.sort方法快速完成数组排序，再进行后续的逻辑。

当然，如果在考察排序算法时（快排、归并排序等），咱肯定是没法用 JDK 中自带的 API 啦。

使用方式

• Arrays.sort(int[] a)：对数组 a 进行排序，使用的是快排算法，时间复杂度为O(n log(n))。当然，除了int型数组以外，其他的数据类型也支持默认的排序。

• Arrays.sort(T[] a, Comparator<? super T> c)：根据传入的比较大小逻辑Comparator对数组 a 进行排序。这种方法更灵活，而且可以支持自定义的对象数组排序。

比如，我要对一个二维数组排序，排序规则是根据第一维度的大小来排序。那么代码如下：

int[][] intervals;
Arrays.sort(intervals, Comparator.comparingInt(a -> a[0]));
1
2

典型题目

• 15. 三数之和：是两数之和的升级版，但是给定的数组并不是升序数组。因此需要将数组进行排序，从最左侧开始将小于 0 的数字的绝对值作为 target，按照两数之和的方式去找另外两个数字。

• 49. 字母异位词分组：用相同的一组字母，按照不同的顺序拼成的多个单词，就是字母异位词。所以，将单词的字符进行排序，来生成新的字符串。字符串相同的单词，就是字母异位词。

• 56. 合并区间：对于这道题，需要从左到右的去将区间依次合并。所以，首先要将数组按照左边界递增的顺序排序，然后再遍历排序后的数组，如果有两两重复的部分，则合并。

• 40. 组合总和 II：这是一道使用回溯法解决的问题。当然，前提也是要先对数组进行排序，然后从小到大遍历数组加和，进行回溯。

2、哈希表

哈希表的使用过于广泛。一般会在解答算法题的过程中，借用哈希表来达成以下目的：

1. 缓存之前计算过的结果，在重复利用时可以提高效率

2. 判断某个数字/字符是否出现过，并统计数量

使用方式

对于简单的场景，如果知道键的取值范围，我们可以使用数组来实现哈希表。下标为 key，数组的值为 value。

例如：

• 在统计小写字母出现次数时，可以用int[] array = new int[26]来初始化一个数组作为哈希表。但是要注意的是，当你取下标时，需要用字符-'a'来计算出正确的下标，否则会出现下标越界的情况。

对于复杂的场景，HashMap更方便易用。HashMap是个太基础常用的数据结构了，这里简单记录一下做题时会用到的比较好用的方法。

• getOrDefault(Object key, V defaultValue)：在取值的时候不需要判空的操作，如果key 不存在，可以指定返回默认值。

• containsKey(Object key)：判断 key 是否存在。

基本就没有其他的特殊的用法了。

典型题目

• 242. 有效的字母异位词：使用哈希表保存两个字符串中每个字符的个数，之后比较即可。

• 49. 字母异位词分组：对每个字符串的字符进行排序，排序后相同的字符串，则互为字母异位词。用一个 value 为List的HashMap保存排序后的字符串与对应的字母异位词的映射关系。

• 146. LRU 缓存：键值对格式的数据结构，需要使用哈希表。本题的底层结构是一个 key 为Integer类型，value 为链表的HashMap结构。

3、栈

栈也是非常常用的数据结构，后进先出的特性，在深度优先遍历二叉树、倒序打印链表等场景时非常实用。

JDK 的 util 包中提供了Stack这个数据结构，但也已经成为历史了。Java 官方更推荐使用Deque来实现栈的功能。Deque是一个双端队列的接口，既可以实现栈的功能，也可以实现队列的功能。

使用方式

当然，无论是使用Stack还是Deque，入栈和出栈的方法名，都是 push、pop、peek。

• push(E e)：将一个元素压入栈顶

• pop()：将元素从栈顶移除，并返回该元素

• peek()：查询并返回栈顶元素，但是不移除

• isEmpty()：使用pop或者peek方法之前，最好是先判空，避免空栈抛异常

典型题目

二叉树前序遍历（中-左-右）

1. 不断的将栈顶节点的左子节点压入栈。入栈之前记录该节点（遍历）

2. 当左子节点为空时，将栈顶节点弹出栈，再将该节点的右子节点压入栈

3. 继续将栈顶节点（刚才压入的右子节点）的左子节点压入栈

二叉树中序遍历（左-中-右）

1. 不断的将栈顶节点的左子节点压入栈。

2. 当左子节点为空时，将栈顶节点弹出栈。记录该节点（遍历），再将该节点的右子节点压入栈

3. 继续将栈顶节点（刚才压入的右子节点）的左子节点压入栈

二叉树后序遍历（左-右-中）

1. 不断的将栈顶节点的左子节点压入栈。

2. 当左子节点为空时，查看栈顶元素，判断是否有右节点。

   1. 存在右子节点，且右子节点没有被记录过，则将该节点的右子节点压入栈，继续重复第一步。
   2. 不存在右节点，记录该节点（遍历），将栈顶节点弹出栈，继续重复第二步。

其他典型题目

栈很适合处理存在对称性的问题，比如成对出现的括号，四则运算等。

• 20. 有效的括号：判断括号合法性的问题，是很经典的栈问题。将字符压入栈，当遇到右括号时，弹出栈顶元素，判断是否可以配成一对即可。

• 150. 逆波兰表达式求值：四则运算是很经典的栈问题，将字符压入栈，遇到运算符号时，将栈顶的两个元素出栈进行计算，再将结果压入栈。

• 224. 基本计算器：这道题对栈的使用，和常规理解的不一样。并不是像波兰表达式那样去将每个字符都入栈。而是用栈来维护每一层的括号前的正负号。当前层括号中的计算，都要根据栈顶的正负来参与加减的结果。

单调栈在处理一些需要比较大小的问题时，比较好用。所谓的单调栈，实际上只是人为的让栈保持单调递增或递减。当入栈的元素破坏单调性时，就需要弹出栈顶元素进行逻辑处理，从而解决问题。

• 739. 每日温度：使用单调栈来保存日期。遍历数组，比较今天的温度是否比栈顶日期对应的温度值高。温度高则出栈处理，这样就可以记录出栈日期到今天的日期差。继续比较直到栈空或者今天温度小于栈顶日期对应的温度值时，将当前日期入栈。

• 84. 柱状图中最大的矩形：将数组下标依次入栈，且使用单调递增栈，即：需要保证栈顶元素下标对应的柱高，一直都是最大的。当遍历到比栈顶下标对应的柱子矮的柱子时，便以栈顶下标作为左边界，以当前下标作为右边界，以栈顶下标对应的柱高作为高，计算矩形面积。继续比较直到栈空或者栈顶下标对应的柱高小于当前柱高时，将当前下标入栈，并继续遍历。

• 42. 接雨水：与第 84 题类似，也可以用单调栈来解答。只不过本题是要维护一个单调递减栈。

4、队列

队列的特性是先进先出。这个特性非常适合二叉树的广度优先搜索、滑动窗口等场景。相比于栈，队列的花样好像并没有很多。

使用方式

队列由Queue接口定义，对于接口的定义而言，入队出队查询方法都有抛异常和不抛异常两种方法：

• 元素入队：add(E e)或者offer(E e)，前者会存在抛异常的情况

• 元素出队：remove()或者poll()，前者会存在抛异常的情况

• 返回队头元素：element()或者peek()，前者会存在抛异常的情况

当然，对于解决算法题的场景，我们其实并不是很在意是否会抛异常，只需要在使用队列时先判空即可。

Queue接口有多个实现，我们常用的队列实现可以使用LinkedList或者ArrayDeque。

典型题目

• 933. 最近的请求次数：使用一个固定长度的队列来处理请求。当新的请求加入队尾时，长度超过了规定的时间范围，则需要将队头的请求出队即可。

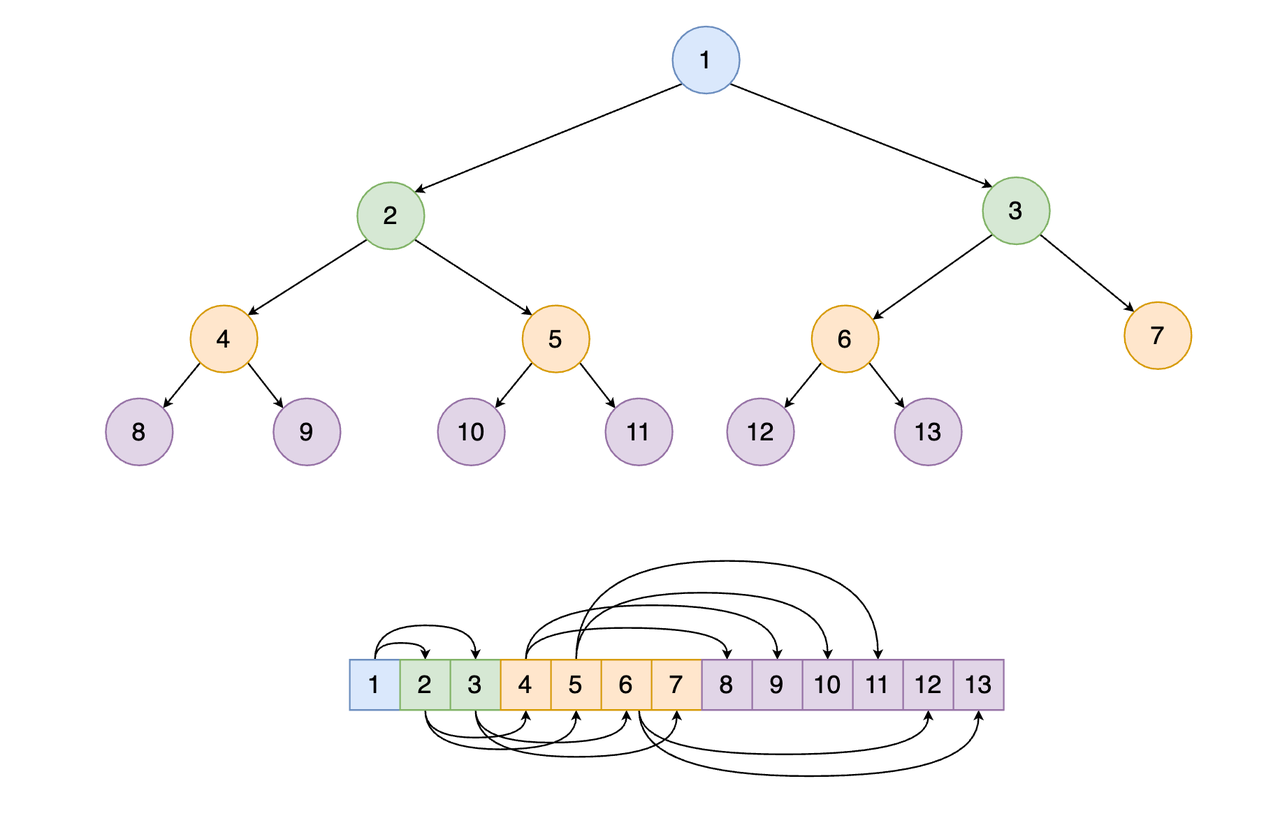
• 102. 二叉树的层序遍历：即考察二叉树的广度优先搜索。实现逻辑：从根节点开始，将节点压入队列。之后不断的出队列，将节点的子节点压入队列，如此往复，直到队列为空。以下题目都是和广度优先搜索相关的题目：513. 找树左下角的值、515. 在每个树行中找最大值、919. 完全二叉树插入器、199. 二叉树的右视图

5、优先队列

优先队列PriorityQueue虽然叫做队列，但是底层是由堆实现。PriorityQueue默认情况下是一个最小堆（小顶堆）。当然，在初始化的时候，也是可以传入自定义的Comparator来实现一个最大堆（大顶堆），或者实现较为复杂的排序逻辑。

因为堆的特性可以对元素进行动态的排序，因此，优先队列常用于需要动态排序的问题中，比如第 K 大、第 K 小、前 K 个这类问题。

使用方式

因为PriorityQueue也是实现了Queue接口，因此 API 和普通队列基本一致。

• PriorityQueue<Integer> priorityQueue = new PriorityQueue<>((o1, o2) -> o2 - o1)：实现一个最大堆

• PriorityQueue<ListNode> pq = new PriorityQueue<>(Comparator.comparingInt(a -> a.val))：实现自定义对象的排序规则

• 加入新的元素：add(E e)或者offer(E e)，add方法实际上是直接调用了offer方法

• 移除堆顶元素并返回：remove()或者poll()，remove方法实际上调用了poll方法，但是如果返回的元素为空时会抛异常

• 查询堆顶元素：element()或者peek()，element方法实际上调用了peek方法，但是如果返回的元素为空时会抛异常

典型题目

• 703. 数据流中的第 K 大元素：所谓第 K 大，实际上就是倒数第 K 小。维护一个最小堆的优先队列，保证队列的长度不大于 K 。不断的加入元素，如果长度大于 K，则移除栈顶元素。此时可以保证栈顶元素即为第 K 大元素。

• 347. 前 K 个高频元素：先计算每个数字出现的频率，然后用优先队列去排序。

• 23. 合并K个升序链表：合并两个升序链表时，可以交替的比较两个头结点的大小。遇到 K 个升序链表时，我们就需要将这 K 个链表的头结点放入到优先队列中，辅助我们找到 K 个节点中最大的值。

总结

再用几句话简单总结一下：

• 需要对数组进行排序时，直接用 API，不用想着一定要自己实现。

• 哈希表常用于记录出现过的元素，以及作为缓存提高效率。简单的哈希表用数组实现即可。

• 栈是非常常用的数据结构，常见于深度优先搜索、处理括号、四则运算等和「层」有关的问题。单调栈也是一个非常常用的解题技巧，常用于在一个图表上框选面积，或者按照顺序比较大小的场景。

• 队列常用于二叉树的广度优先搜索和滑动窗口问题。

• 优先队列方便我们解决动态的，多个数据源的排序问题，随时将前 K 大（或小）的元素掌握在手心。