【优化选址】基于matlab遗传算法求解物流配送中心选址【含Matlab源码 1917期】

一、物流选址简介

1 引言
配送中心是物流系统网络中的关键节点和重要的基础设施，在整个物流系统网络规划中起着枢纽性的作用[1]。快递物流配送中心选址是指在具有若干个发件网点或者若干个收件网点的物流配送区域内，综合考虑物流运输成本、配送中心建设成本等成本因素，采用定性与定量分析方法，选取最符合经济社会情况的单个或者多个位置设置配送中心的物流系统网络规划过程。在整个快递物流供应链环节中，快递配送中心，对上承接来自发件网点包裹的集运任务，对下承接收件网点的配送运输任务，其选址结果将会对配送路径的规划、运营成本、配送效率等产生直接的影响。

2 研究综述
基于配送中心对国家流通经济发展的重要作用，国内学者们针对各种类型的配送中心的选址问题，分别采用不同的算法模型，对其进行了深入研究：如李茂林认为物流配送中心选址难以优化以至于会影响整个物流系统的配送效率，针对这一问题他提出一系列的猴群优化算法求解策略，对模型进行求解，通过对线性函数表达式中多个影响因子的非线性调节，改进了猴群算法的爬行过程，提高了算法模型的求解精度和求解能力，最终更加精确地求解出物流配送中心优化选址位置；张于贤等通过构建带有物流收益(输出)和物流成本(输入)之差的数据包络评估模型(data envelopment evaluation analysis，DEA)，对现有配送中心的各项指标进行评估，根据评估的结果得到配送中心的再选址方案，但其基于DEA选址方法所构建的线性函数选址评价模型与通常利用CCR模型、BCC模型等具有矩阵性质的评价模型方法不同，该选址评价研究方法的可行性有待进一步实证；崔杨等针对第三方物流配送过程中产生的如延误、爆仓等配送异常问题，综合运用层次分析法中的定性分析方法和定量分析方法，对第三方物流配送中心选址问题进行了评价研究，通过构造层次分析模型、判断矩阵，求解出最优位置作为第三方物流配送中心的选址位置；于蕾综合采用定性与定量分析法对安徽省农产品的供给与需求状况进行了分析，构建了基于重心法的农产品配送中心选址模型，并采用R语言编程对具有迭代性质的选址模型进行求解，但存在绝对假设条件限制、去市场化、需求量计算过于简单等局限性；生力军[6]指出，经典粒子群选址模型在求解过程中存在局部最优和过早收敛等问题，为了克服此缺点，将量子进化算法与粒子群算法相结合，构建了基于量子粒子群算法的物流配送中心选址模型，并通过粒子编码和量子交换、变异等操作，有效避免了模型在选址求解中存在局部最优和过早收敛等问题。

基于遗传算法选址国内学者们针对不同类型的选址问题进行了大量创新性的研究：如赵斌等指出，传统单一的遗传算法难以快速有效求解出系统复杂的医疗器械物流园区选址问题的最优化问题，通过将遗传算法和免疫算法相结合，建立了免疫遗传算法的选址模型，针对医疗器械物流园区选址的特点，构建了包含多种成本要素的医疗器械物流园区选址问题的目标函数模型，并且对选址模型的求解方法进行了设计，从而求解出最优的物流园区选址方案；郭静文等为了优化消防站网络规划布局结构、降低消防站选址的系统选址成本，以及提升消防站空间资源利用率，对传统的遗传算法进行了改进，使其具有自适应性质，可自行求解出优化后的消防站规划建设个数和选址位置，有效克服了在已有选址规划方案中选择消防站建设个数和选址位置等的缺陷，但在实证研究中，并未给出具体的求解方法或求解过程；周思育等为了解决湖北省内烟草资源物流配送不均衡和配送成本高昂等的问题，构建了综合考虑多种选址成本要素的遗传算法选址模型，并且通过Matlab数据分析软件，对配送中心选址模型进行求解，选取最佳的位置设置配送中心，提高了烟草资源物流配送的效率，并降低了配送中心系统选址的成本；张钰川等为兼顾物流园的配送运输、货物集散、仓储分拨、管理服务等的作用和功能，基于物流成本的基础上，构建了带有双层规划的遗传算法物流园选址模型：上层模型由影响物流园选址要素的各种成本函数所构成，下层模型由影响决策者和客户利益诉求的成本函数所构成，并通过遗传算法对双层规划模型进行求解，最后通过实例验证了遗传算法模型对物流园选址成本问题具有一定的优化作用。

本文选择利用遗传算法模型对快递物流配送中心的选址问题进行研究，针对配送中心选址的特点，构建了包含固定成本、分拣成本等多个成本要素的线性目标函数，建立了基于遗传算法的选址模型。遗传算法选址问题属于NP难题，利用传统的算法求解方法容易产生局部最优等问题，为了克服遗传算法模型在选址问题求解过程中所产生的局部收敛和早熟收敛等局限性，本文提出了一系列经过改进后的遗传算法求解策略，具体包括编码方法、自适应交叉概率函数、自适应变异概率函数等求解方法，这在很大层度上提高了遗传算法模型在选址问题中的求解精度和求解效率。

3 遗传算法的配送中心选址模型
3.1 模型假设
为了便于构建快递物流配送中心遗传算法选址模型，简化算法模型计算复杂性和使其具有很好的适用性，现对模型做如下假设：

1)在一定备选范围内进行配送中心的选取；

2)发件网点或收件网点数目多于配送中心数目；

3)一个网点仅由一个配送中心提供配送服务，但一个配送中心可覆盖多个网点；

4)配送中心容量可满足各配送网点的总需求量；

5)各网点配送需求一次性运输完成，且假设匀速行驶；

6)物流系统中包含两个层次的运输，即从发件网点到配送中心的运输和从配送中心到收件网点的运输，且均采用公路运输；

7)系统总费用不考虑包裹在分拣中心的装卸搬运成本和暂存成本，只考虑配送中心建设成本、运输费用和变动成本。

3.2 变量设置
假设发件网点数量有m个，配送中心数量有n个，收件网点数量有l个。其他参数符号及变量设置如表1所示。

表1 变量设置

3.3 模型构建

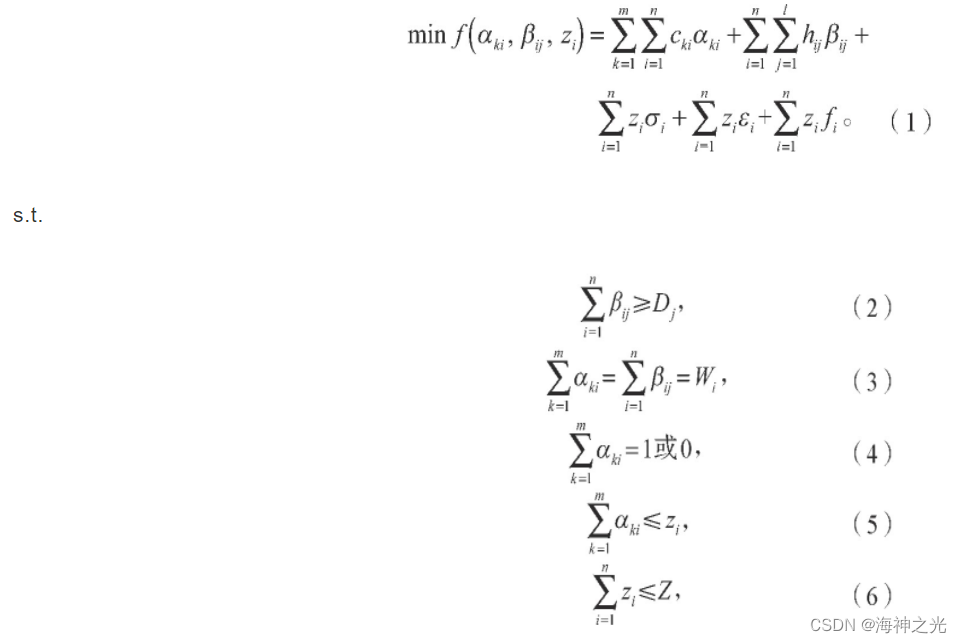
zi=1或0，(7)
αki,βij≥0，(8)
式中：i=1,2,…,n；
k=1,2,…,m；
j=1,2,…,l。

在上述各式中，式(1)表示目标函数，等号右边第1项为从发件网点到配送中心的运输成本，第2项为从配送中心到收件网点的运输费用，第3项为建设配送中心的固定投资成本，第4项和第5项为配送中心的变动成本(分别为管理成本和分拣成本)；式(2)表示配送中心可以满足所有收件网点的配送需求；式(3)表示从收件网点到配送中心的集运量恒等于从配送中心到收件网点的配送量；式(4)表示所有发件网点被配送中心所覆盖；式(5)表示从发件网点到配送中心的运输量小于等于配送中心的最大容量限制即流量限制；式(6)表示配送中心的建设数量不大于其最大建设数量；式(7)(8)为决策变量的约束。

4 基于遗传算法模型的求解
遗传算法(gentic algorithm，GA)这一术语于20世纪50年代由美国学者J.Holland所提出，是基于模拟自然选择和遗传机制的典型启发式算法模型，具有操作简单、鲁棒性强等优点。

在使用遗传算法对快递物流配送中心选址问题的求解过程中，容易产生过早收敛和局部最优等问题。为了提高算法模型的全局搜索能力以及保证种群的多样性，防止遗传算法在求解的过程中出现过早收敛和局部最优问题，需要对传统的遗传算法求解进行改进。因此本文提出了一系列的遗传算法选址模型的改进求解策略，从对染色体的编码策略的选择到自适应变异概率的计算，这些求解策略有效解决了传统遗传算法出现的过早收敛和局部最优问题，使GA空间搜索能力明显增强，提高了算法模型的求解能力和求解效率。

4.1 遗传算法模型求解策略
1)染色体编码
将所需要解决的问题采用编码的方式是遗传算法的重要操作，即将求解的问题映射为编码问题，遗传算法中常见的编码方法有二进制编码、格雷编码、排列编码和浮点数编码等。对编码的性质进行评价的指标主要有完备性、健全性和非冗余性。

对于决策变量zi，课题组采用二进制编码[12]方法，利用{0,1}自然数，将配送中心zi通过二进制编码成为由{0,1}所构成的染色体或个体，编码串即染色体的长度L和数量K是由所要求解的精确度来确定的。二进制编码方式具有操作方便、计算简单等优点，但也存在求解精度低、易造成算法搜索空间过大等缺点，且不适应于连续函数问题的编码。

单一的编码方式无法将所有优化问题的决策变量约束表示出来，对于决策变量αki、βij，由于其对应的变量个数比较多，且编码串的长度由决策变量中的变量个数所决定，所以对其采用浮点编码的方法，使得编码后染色体的长度L不至于太长，增强了算法模型的空间搜索能力，有利于算法解码。浮点编码适用于对于求解要求精度较高、具有较大的搜索空间、需要处理复杂的决策变量及约束等特点的编码方法，它降低了遗传算法编码后计算的复杂性，提高了遗传算法的求解效率。

2)适应度函数
为了保证染色体中具有优良性质的个体基因遗传到下一代，通过模拟遗传进化过程中适者生存原理，建立唯一具有评价群体生存选择机会大小的适应度函数，适应度函数值越大，则种群中优良基因作为父代基因遗传到下一代的可能性越大；否则可能性越小。根据这种优化原理，建立如下与目标函数之间存在映射关系的适应度函数：

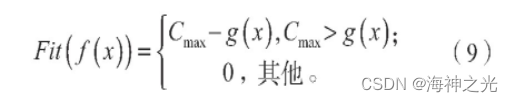
式中：Fit(f(x))为适应度函数；

Cmax表示截止当前进化进度(代数)所产生的g(x)的最大值，此时Cmax会随着进化进度(代数)的变化而变化；

g(x)为目标函数的期望值。

3)选择算子
选择算子操作，通过所构建的适应度函数，可以对群体中染色体遗传性质的优劣进行判断和评价，选择或复制那些群体中适应度值高的个体作为父代基因遗传到下一代，而适应度值低的个体则被淘汰，这种操作有效提高了算法的收敛性和计算效果。本文采用轮盘赌的方法进行选择算子操作[13]，建立如下与适应度函数之间存在映射关系的选择概率：

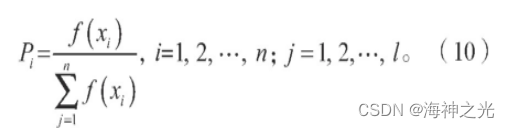
式中：Pi表示个体i被选择的概率；

f(xi)表示各染色体个体的适应度函数值；

xi表示种群中的个体。

4)自适应交叉算子操作
交叉算子模仿自然进化过程中的遗传规律，将具有优良基因的两个父代染色中的部分基因通过交叉算子操作的方式进行基因重组，从而产生新的更适应于适应度函数值的子代个体，交叉算子操作是遗传算法中的核心操作步骤。交叉操作具有随机性和多样性等特点，其类型主要包括单点交叉、多点交叉、部分匹配交叉、顺序交叉等。

交叉算子操作中的交叉概率是影响遗传算法性能的关键所在，对算法的收敛性产生直接的影响。交叉概率越大，染色体产生交叉的速度越快，则其产生新的个体的速度也越快。当交叉概率过大时，在迭代初期会增强算法的搜索能力使其快速收敛，但在迭代后期对具有较高适应度函数值的个体基因的结构破坏性会增大，不利于算法最优解的产生；交叉概率过小时，算法的搜索能力即交叉操作能力过于缓慢，同样不利于寻求算法的最优解。基于这种优化问题，本文引入了自适应交叉概率，计算过程中交叉概率会随着适应度函数值的不同而自动调整，具体的计算公式如下：

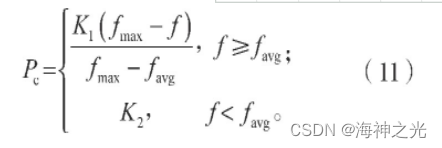
式中：Pc为自适应交叉概率；
fmax为群体中个体为最大的适应度函数值；
favg为每代群体的平均适应度函数值；
f为产生交叉的两个个体其中一个个体为较大的适应度函数值；
K1、K2为区间为(0,1)的常数。

5)自适应变异算子操作
变异算子操作是模仿自然基因在遗传过程中发生基因突变现象，即某条染色体中的一个或者多个基因发生变异的现象，但一般发生变异的概率比较小(通常在为0.01～0.10)。当变异概率太小时，不利于染色体新个体结构的产生；当变异概率太大时，染色体结构遭到破坏的可能性会增大，遗传算法搜索的有效性随之降低。针对变异算子操作中的寻优问题，本文采用自适应变异概率：

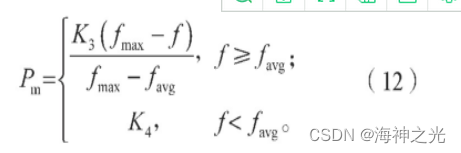
式中：Pm为自适应变异概率；
K3、K4为区间(0,1)的常数。

4.2 遗传算法求解步骤
STEP 1 染色体编码。随机产生K条染色体，并通过二进制的方法进行编码，每条染色体即代表一种可行解。
STEP 2 群体初始化。建立适当规模的由染色体或个体所构成的初始化群体。
STEP 3 适应度函数。适应度函数值是判断个体生存机率大小的唯一标准，对群体进化进度和形势具有直接的影响，可利用式(9)计算出适应度函数值f(xi)。
STEP 4 选择算子。对于种群中适应度高的个体进行操作选择，可直接作为父代染色体进行繁殖，其他的染色体则采用轮盘赌的方式操作选择。
STEP 5 交叉算子。对于被选中的染色体，通过交叉算子操作，将具有优良性质的两个染色体中的部分基因通过交叉位移的方式产生新的个体，并利用式(11)计算出不同个体的自适应交叉概率Pc。
STEP 6 变异算子。对不同的个体采取自适应调整策略，利用式(12)计算出自适应变异概率Pm。
STEP 7 判断适应度函数值。完成STEP 6后跳转至STEP 3，重新计算适应度函数值并作出判断，然后继续进行循环求解。
STEP 8 终止条件：根据预先设定的最大迭代次数Tmax，当达到所规定的迭代规模后则终止算法运行。

二、部分源代码

%% 遗传算法 优化函数
clc;close all;clear all;%清除变量
rand('seed', 100);

global XY p nodenumber maxlink;
filename='需求点分布.xlsx';
[adata,bdata,cdata]=xlsread(filename);
XY=adata(2:end,:)';
nodenumber=size(XY,1);
p=4;% 配送中心个数
maxlink=5;% 最大连接数

N=p*2;%优化问题
lb=[min(XY(:,1))*ones(1,p),min(XY(:,2))*ones(1,p)];
ub=[max(XY(:,1))*ones(1,p),max(XY(:,2))*ones(1,p)];


% 遗传算法参数
popsize=200;%遗传算法种群数
ga_max=500;%遗传算法迭代次数
PM=0.05;%变异概率
PC=0.8;%交叉概率

%% 遗传算法主程序
%性能跟踪
tracemat=zeros(ga_max,2);
gen=0;
tic;
Chrom=genChrome(popsize,N,lb,ub);% 建立种群
Value=decodingFun(Chrom,popsize);%解码染色体
%% 遗传算法优化的主循环
%进度条
wait_hand = waitbar(0,'run……', 'tag', 'TMWWaitbar');
while gen<ga_max
    %% 遗传算法选择
    FitnV=ranking(Value);%分配适应度值
    Chrom=select('rws',Chrom,FitnV,1);%选择
    Chrom=mutationGA(Chrom,popsize,PM,N,lb,ub);% 种群变异,单点变异
    Chrom=crossGA(Chrom,popsize,PC,N);% 种群交叉,单点交叉
    Value= decodingFun(Chrom,popsize);%解码染色体
    %% 计算最优
    [v1,index1]=min(Value);
    gen=gen+1;
    tracemat(gen,2)=mean(Value);
    %% 记录最优
    if gen==1
        bestChrom1=Chrom(index1,:);%记录最优染色体
        bestValue1=v1;%记录的最优值
    end
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

三、运行结果

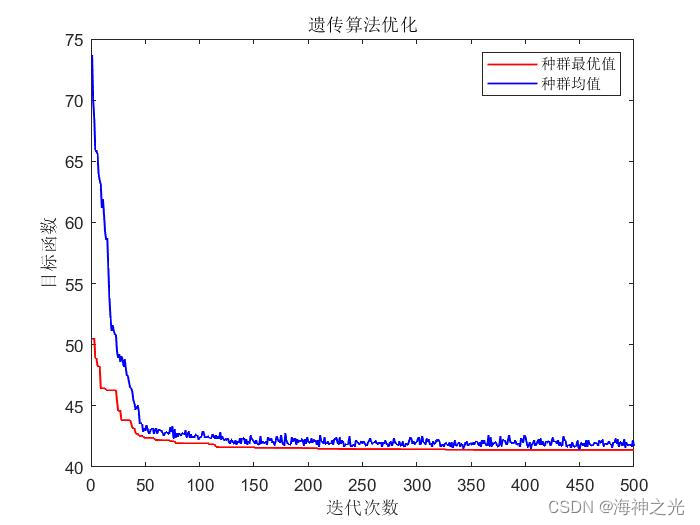
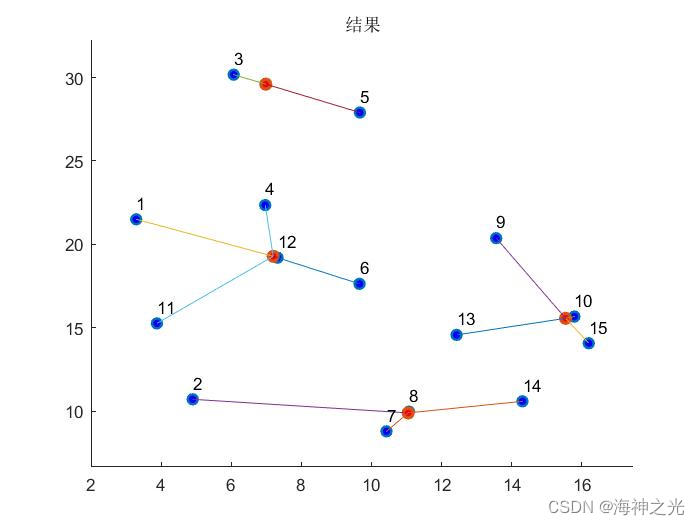
四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.
[3]刘善球,樊兵鹏.基于遗传算法的快递物流配送中心选址[J].湖南工业大学学报. 2021,35(05)

3 备注
简介此部分摘自互联网，仅供参考，若侵权，联系删除