547. 省份数量 - 力扣（LeetCode）

一、题目

有 n 个城市，其中一些彼此相连，另一些没有相连。如果城市 a 与城市 b 直接相连，且城市 b 与城市 c 直接相连，那么城市 a 与城市 c 间接相连。

省份 是一组直接或间接相连的城市，组内不含其他没有相连的城市。

给你一个 n x n 的矩阵 isConnected ，其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连，而 isConnected[i][j] = 0 表示二者不直接相连。

返回矩阵中 省份 的数量。

示例 1：
 

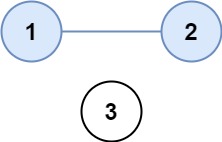
输入：isConnected = [[1,1,0],[1,1,0],[0,0,1]]
输出：2

示例 2：

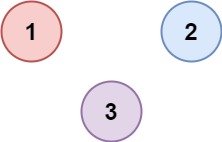
输入：isConnected = [[1,0,0],[0,1,0],[0,0,1]]
输出：3

提示：

• 1 <= n <= 200
• n == isConnected.length
• n == isConnected[i].length
• isConnected[i][j] 为 1 或 0
• isConnected[i][i] == 1
• isConnected[i][j] == isConnected[j][i]

二、代码

class Solution {
    public int findCircleNum(int[][] isConnected) {
        // 判空
        if (isConnected == null) {
            return 0;
        }
 
        // 获取二维数组有多少行，也就是有多少个城市
        int n = isConnected.length;
        // 创建并查集，并查集大小为n
        UnionFind unionFind = new UnionFind(n);
        // 遍历二维数组的上半部分，因为城市a和城市b联通，那么b一定也和a联通，所以只需要遍历二维数组的一半就够了，二维数组是关于对角线对称的
        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n; j++) {
                // 如果i和j两个城市联通，则使用并查集将他们两个合并到一个集合中
                if (isConnected[i][j] == 1) {
                    unionFind.union(i, j);
                }
            }
        }
        // 返回并查集当下的集合数
        return unionFind.count();
    }
 
    // 并查集
    public static class UnionFind {
        // 记录每个结点的父节点，经过路径压缩之后，就变成了记录每个集合的代表节点  parents[i] = k  表示i的代表节点是k，如果parents[i] = parents[j],就说明i和j在同一个集合中
        private int[] parents;
        // 记录每一个集合中有多少个元素。 size[i] = k ： 只有当i是代表节点时，size[i]才有意义，否则无意义
        private int[] size;
        // 栈，用来做路径压缩
        private int[] stack;
        // 记录当前并查集中有多少个集合
        private int cnt;
 
        // 初始化并查集
        public UnionFind(int n) {
            parents = new int[n];
            size = new int[n];
            stack = new int[n];
            // 最开始将每一个点都看作是独立的集合，有n个点则并查集集合数就有n个
            cnt = n;
 
            // 最开始将每一个点都看作是一个独立的集合，在后续并查集合并操作的过程中再将他们进行合并
            // {0} {1} {2} {N-1}
            for (int i = 0; i < n; i++) {
                // 每个人的父节点就是自己
                parents[i] = i;
                // 每个集合的元素数为1
                size[i] = 1;
            }
        }
 
        // 找到i的代表节点，并进行路径压缩
        public int find(int i) {
            int index = 0;
            // 先将途径的所有节点加入到栈中
            stack[index++] = i;
            // 沿着父节点路径进行遍历，直到遍历到最末尾，也就是节点的父节点等于其本身时
            while (parents[i] != i) {
                i = parents[i];
                // 这个过程中将路过的所有节点都加入到栈中
                stack[index++] = i;
            }
            // 上述循环结束后，i即为最后找到的代表节点
 
            // 进行路径压缩，将经过的所有节点的父节点直接设置为他们的代表节点
            while(index > 0) {
                parents[stack[--index]] = i;
            }
 
            // 返回代表节点
            return i;
        }
 
        // 进行合并
        public void union(int i, int j) {
            // 找到两个点的代表节点
            int iparent = find(i);
            int jparent = find(j);
 
            // 得到两个点所在集合的元素数
            int isize = size[iparent];
            int jsize = size[jparent];
 
            // 如果两个点的代表节点不同，则说明连个点现在不在同一个集合中，所以需要对他们进行合并操作
            if (iparent != jparent) {
                // 将小集合挂在大集合上，这样也能有效地减少父节点路径长度，提高效率
                if (isize > jsize) {
                    parents[jparent] = iparent;
                    // 更新集合的元素个数
                    size[iparent] += size[jparent];
                } else {
                    parents[iparent] = jparent;
                    size[jparent] += size[iparent];
                }
                // 合并之后就将并查集中集合的数量减1
                cnt--;
            }
        }
 
        // 返回并查集中集合的数量
        public int count() {
            return cnt;
        }
    }
}

三、解题思路 

这种求连通性的题目，一般都是用并查集取求解。就是创建并查集，然后对两个节点进行合并操作，有相同代表节点的点则说明是相互连通的，所以最后并查集中在同一个集合中的点都是相互连通的。