-
矩阵分析与应用
向量的相似度
考虑M个类型的模式,它们分别被记作
 。假定通过已知类型属性的观测样本,抽取出M个模式向量
。假定通过已知类型属性的观测样本,抽取出M个模式向量 ,给定一任意的未知模式向量x,希望判断它归属于哪一类模式,这个问题就被称为模式分类,是模式识别的基本问题之一。
,给定一任意的未知模式向量x,希望判断它归属于哪一类模式,这个问题就被称为模式分类,是模式识别的基本问题之一。模式分类的基本思想是将未知的模式向量x同M个样本模式向量进行比对,看x与哪一个样本模式向量最相似,并据此作出模式分类的判断。
假定
 分别作为未知模式向量x与已知样本模式向量
分别作为未知模式向量x与已知样本模式向量 之间的相似关系的符号。以x与
之间的相似关系的符号。以x与 的相似关系为例,若
的相似关系为例,若
则称未知模式向量x与样本模式向量
 更相似,为了建立这种相似关系,需要定义相似度或者相异度。
更相似,为了建立这种相似关系,需要定义相似度或者相异度。接下来介绍五种相似度。
Euclidean距离
最简单的且最直观的相似度是两个向量之间的Euclidean距离,未知模式向量x与第i个模式向量
 之间的Euclidean距离记作
之间的Euclidean距离记作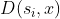 ,定义为:
,定义为:
若

则
 是到x的近邻(即最近的邻居)
是到x的近邻(即最近的邻居)
近邻分类法作为一种广泛使用的分类法,它将未知类型的模式向量x归为它的近邻所属的模式类型。Mahalanobis距离
除了Euclidean距离外,还有一个距离函数是Mahalanobis距离。令:

代表N个样本模式向量的均值向量,并使用

表示N个样本模式向量的协方差矩阵。
从未知模式向量x到均值向量m之间的Mahalanobis距离定义为:

类似地,从第i个样本模式向量
 到均值向量m的Mahalanobis距离定义为:
到均值向量m的Mahalanobis距离定义为:
根据近邻分类法,将未知模式变量x归为满足

的近邻
 所属的模式类型。
所属的模式类型。夹角余弦
两个向量之间的相似度的测度不一定局限于距离函数。两个向量的夹角的余弦函数:
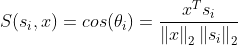
这也是相似度的一种有效测度,若
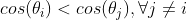 成立,则认为未知模式向量x与样本模式向量
成立,则认为未知模式向量x与样本模式向量 最相似。
最相似。Tanimoto测度
Tanimoto测度:

Tanimoto测度广泛应用于信息恢复,疾病分类,动植物分类等领域。
目标-概念距离
待分类的信号称为目标信号,分类通常是根据某种物理或者几何概念进行的。令X为目标信号,
 代表第i类目标的分类概念,于是有以下关系:
代表第i类目标的分类概念,于是有以下关系:
这类有效关系一般用目标-概念距离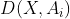 来描述,因此若目标-概念距离
来描述,因此若目标-概念距离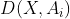 最小,则将X归为第i类目标
最小,则将X归为第i类目标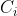 。
。 -
相关阅读:
JVM 高级面试题及答案整理,最新面试题
【JVM】并发可达性分析-三色标记算法
板带纠偏控制系统伺服比例阀放大器
JSP 购物商城系统eclipse定制开发mysql数据库BS模式java编程servlet
【仿牛客网笔记】Spring Boot实践,开发社区登录模块-显示登录信息
为什么客户端和服务器不支持SSL协议
【Java 进阶篇】Session 使用详解
shopee平台现在好做吗
MySQL数据库的简介及select语句的执行流程
golang中出于性能考虑的那些实用代码片段 |字符串篇
- 原文地址:https://blog.csdn.net/weixin_46007132/article/details/125507983