-
卷积神经网络——inception网络及python实现
1、简介
Inception 网络是卷积神经网络发展史上一个重要的里程碑。在 Inception 网络出现之前,大部分流行卷积神经网络都是把卷积层堆叠得越来越多,使网络越来越深,来对特征进行多次处理,以此希望能够得到更好的性能。Inception网络对输入图像进行并行采集特征,并将所有输出结果拼接为一个非常深的特征图,由于并行提取特征时卷积核大小不一样,这也就在一定程度上丰富了特征,使特征多样化。
2、inception网络结构

类似上述这种并行采集信号特征的方式,输入一张图片进来,会有1*1、3*3、5*5等不同大小的卷积核进行特征提取。这样,网络中每一层都能学习到“稀疏”(3x3、5x5)或“不稀疏”(1x1)的特征,既增加了网络的宽度,也增加了网络对尺度的适应性。使用1x1的卷积核实现降维操作,以此来减小网络的参数量。
网络结构CBAPD如下:

可以看出卷积都是使用全零填充,而激活函数都是 relu,基本都是CPA的结构,没有池化层和丢失层。
3、python实现
采用的数据集还是fashion数据集,可以自己去深刻了解。
主要结构:
- class ConvBNRelu(Model):
- def __init__(self, ch, kernelsz=3, strides=1, padding='same'):
- super(ConvBNRelu, self).__init__()
- self.model = tf.keras.models.Sequential([
- Conv2D(ch, kernelsz, strides=strides, padding=padding),
- BatchNormalization(),
- Activation('relu')
- ])
- def call(self, x):
- x = self.model(x, training=False)
- return x
- class InceptionBlk(Model):
- def __init__(self, ch, strides=1):
- super(InceptionBlk, self).__init__()
- self.ch = ch
- self.strides = strides
- self.c1 = ConvBNRelu(ch, kernelsz=1, strides=strides)
- self.c2_1 = ConvBNRelu(ch, kernelsz=1, strides=strides)
- self.c2_2 = ConvBNRelu(ch, kernelsz=3, strides=1)
- self.c3_1 = ConvBNRelu(ch, kernelsz=1, strides=strides)
- self.c3_2 = ConvBNRelu(ch, kernelsz=5, strides=1)
- self.p4_1 = MaxPool2D(3, strides=1, padding='same')
- self.c4_2 = ConvBNRelu(ch, kernelsz=1, strides=strides)
- def call(self, x):
- x1 = self.c1(x)
- x2_1 = self.c2_1(x)
- x2_2 = self.c2_2(x2_1)
- x3_1 = self.c3_1(x)
- x3_2 = self.c3_2(x3_1)
- x4_1 = self.p4_1(x)
- x4_2 = self.c4_2(x4_1)
- # concat along axis=channel
- x = tf.concat([x1, x2_2, x3_2, x4_2], axis=3)
- return x
- class Inception(Model):
- def __init__(self, num_blocks, num_classes, init_ch=16, **kwargs):
- super(Inception, self).__init__(**kwargs)
- self.in_channels = init_ch
- self.out_channels = init_ch
- self.num_blocks = num_blocks
- self.init_ch = init_ch
- self.c1 = ConvBNRelu(init_ch)
- self.blocks = tf.keras.models.Sequential()
- for block_id in range(num_blocks):
- for layer_id in range(2):
- if layer_id == 0:
- block = InceptionBlk(self.out_channels, strides=2)
- else:
- block = InceptionBlk(self.out_channels, strides=1)
- self.blocks.add(block)
- # enlarger out_channels per block
- self.out_channels *= 2
- self.p1 = GlobalAveragePooling2D()
- self.f1 = Dense(num_classes, activation='softmax')
- def call(self, x):
- x = self.c1(x)
- x = self.blocks(x)
- x = self.p1(x)
- y = self.f1(x)
- return y
- model = Inception(num_blocks=2, num_classes=10)
添加库和读取数据集 :
- import tensorflow as tf
- import os
- import numpy as np
- from matplotlib import pyplot as plt
- from tensorflow.keras.layers import Conv2D, BatchNormalization, Activation, MaxPool2D, Dropout, Flatten, Dense, \
- GlobalAveragePooling2D
- from tensorflow.keras import Model
- np.set_printoptions(threshold=np.inf)
- fashion = tf.keras.datasets.fashion_mnist
- (x_train, y_train), (x_test, y_test) = fashion.load_data()
- x_train, x_test = x_train / 255.0, x_test / 255.0
- x_train = x_train.reshape(x_train.shape[0], 28, 28, 1)
- x_test = x_test.reshape(x_test.shape[0], 28, 28, 1)
迭代求解并绘图:
- model.compile(optimizer='adam',
- loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=False),
- metrics=['sparse_categorical_accuracy'])
- cp_callback = tf.keras.callbacks.ModelCheckpoint(filepath=checkpoint_save_path,
- save_weights_only=True,
- save_best_only=True)
- history = model.fit(x_train, y_train, batch_size=128, epochs=20, validation_data=(x_test, y_test), validation_freq=1,
- callbacks=[cp_callback])
- model.summary()
- acc = history.history['sparse_categorical_accuracy']
- val_acc = history.history['val_sparse_categorical_accuracy']
- loss = history.history['loss']
- val_loss = history.history['val_loss']
- plt.subplot(1, 2, 1)
- plt.plot(acc, label='Training Accuracy')
- plt.plot(val_acc, label='Validation Accuracy')
- plt.title('Training and Validation Accuracy')
- plt.legend()
- plt.subplot(1, 2, 2)
- plt.plot(loss, label='Training Loss')
- plt.plot(val_loss, label='Validation Loss')
- plt.title('Training and Validation Loss')
- plt.legend()
- plt.show()
结果如下图:
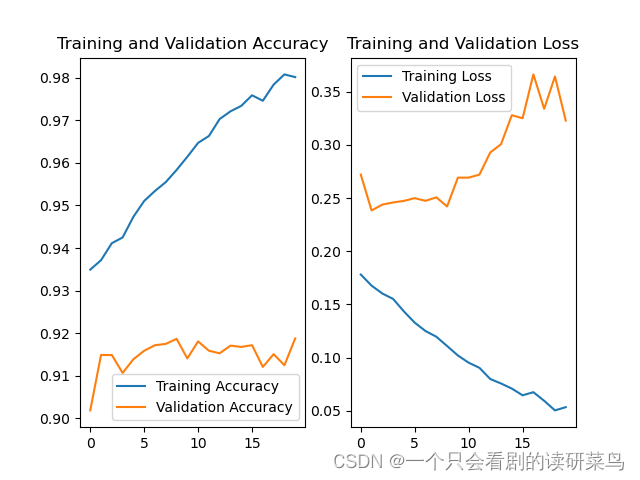
-
相关阅读:
【LeetCode】701.二叉搜索树中的插入操作
看的是SpringBoot连接mysql数据,写入数据
MySQL 多种查询方法
MacOS 控制固态磁盘写入量,设置定时任务监控
人工智能数学基础之线性代数(三)
字符串匹配之Sunday算法
GDB调试C/C++程序
极智开发 | 阿里云ECS本地开发环境搭建
k8s-权限管理
微软Azure配置中心 App Configuration (二):Feature Flag 功能开关特性
- 原文地址:https://blog.csdn.net/abc1234abcdefg/article/details/125504377
