前言

关于各种集成模型，已经有很多文章做了详细的原理介绍。本文不再赘述stacking的原理，直接通过一个案例，使用stacking集成模型预测回归问题。
本文通过学习一篇stacking继承学习预测分类问题，对其代码进行了调整，以解决回归问题。

代码与解析

导包

使用KFold进行交叉验证
stacking基模型包含4种（GBDT、ET、RF、ADA）
元模型为LinearRegression
回归模型评价指标为r2_score

from sklearn.model_selection import KFold
from sklearn.model_selection import train_test_split
from sklearn.ensemble import GradientBoostingRegressor as GBDT
from sklearn.ensemble import ExtraTreesRegressor as ET
from sklearn.ensemble import RandomForestRegressor as RF
from sklearn.ensemble import AdaBoostRegressor as ADA
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
import numpy as np
import pandas as pd
1
2
3
4
5
6
7
8
9
10

关于为何使用KFold，这篇文章提到：
KFlod 适用于用户回归类型数据划分
stratifiedKFlod 适用于分类数据划分
并且在实验中也发现，stratifiedKFlod.split(X_train,y_train)的y_train不可为连续数据，因此无法使用，只能用KFold

数据载入

读取文件并用train_test_split划分数据集。划分后的数据类型为Dataframe，而由于后续使用array方便一点，所以划分之后需要进行数据转换。同时需要记录下Dataframe的列名，后续还会用到。

df = pd.read_csv("500.csv")
X = df.iloc[:, :6]
y = df.iloc[:, -1]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
X_cols = X_train.columns
X_train = X_train.values
y_train = y_train.values
X_test = X_test.values
1
2
3
4
5
6
7
8

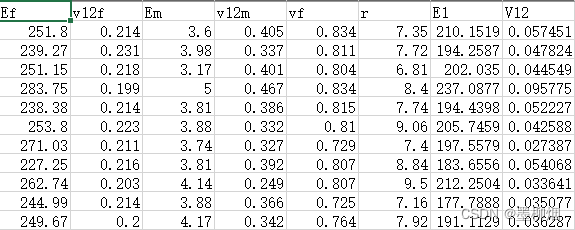
原数据（500.csv）如下图，有500个样本，前六个参数为特征，最后两个为输出。为简便起见，本案例只研究通过前六个特征预测最后一列输出。X_train为（400，6）

第一层模型

models = [GBDT(n_estimators=100),
          RF(n_estimators=100),
          ET(n_estimators=100),
          ADA(n_estimators=100)]

X_train_stack = np.zeros((X_train.shape[0], len(models)))
X_test_stack = np.zeros((X_test.shape[0], len(models)))
1
2
3
4
5
6
7

这里，新建了两个ndarray，可见其大小为（400,4）和（100,4）。
结合stacking的原理来理解：
对每个模型的X_train进行了交叉验证，结束后会得到（400,1）大小的预测值。4个模型则为（400,4），作为第二层模型训练数据的输入。
交叉验证的同时每一折也会得到对X_test的预测，最后求平均得到（100,1）大小的预测值，4个模型则为（100,4），作为第二层模型test数据的输入。

第一层训练并且得到第二层所需数据

# 10折stacking
n_folds = 10
kf = KFold(n_splits=n_folds)

for i, model in enumerate(models):
    X_stack_test_n = np.zeros((X_test.shape[0], n_folds))

    for j, (train_index, test_index) in enumerate(kf.split(X_train)):
        tr_x = X_train[train_index]
        tr_y = y_train[train_index]
        model.fit(tr_x, tr_y)
        
        # 生成stacking训练数据集
        X_train_stack[test_index, i] = model.predict(X_train[test_index])
        X_stack_test_n[:, j] = model.predict(X_test)

    # 生成stacking测试数据集
    X_test_stack[:, i] = X_stack_test_n.mean(axis=1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

首先是第一层i循环，是对4个模型循环。
这里新定义了X_stack_test_n用于存储10折交叉验证中，每折对X_test（100,6）的预测，得到（100,1）的结果。存储10次后大小为（100,10）。可以看到最后一行代码对该10列数据求了平均数，得到（100,1）的数据。最终4个模型得到（100,4），作为第二层模型test数据的输入。

然后再看第二层j循环，是在进行10折交叉验证。
train_index, test_index分别记录了每折验证时的训练与测试编号。如果没有设置shuffle=True，则为0-399个数据依次而不是随机取40个作为测试集划分。由于我原本的数据就比较随机分布，所以这里洗不洗牌无所谓。
由于之前转换了X_train数据类型为array，所以这里可以直接tr_x = X_train[train_index]将对应位置的数据取出。
通过train_index取出的数据进行模型训练，通过test_index取出的数据进行模型预测。
倒数二三行的代码将预测的结果分别给到了之前新建的array里。

第二层模型训练

model_second = LinearRegression()
model_second.fit(X_train_stack,y_train)
pred = model_second.predict(X_test_stack)
print("R2:", r2_score(y_test, pred))
1
2
3
4

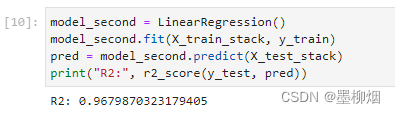
到这里就很清晰了，第二层训练很简单。
训练的输入使用X_train_stack（400,4）,y_train（400,1）
训练好的模型测试一下X_test_stack（100,4）得到结果pred（100,1）
然后获得评估指标r2_score即可

基模型指标

# GBDT
model_1 = models[0]
model_1.fit(X_train,y_train)
pred_1 = model_1.predict(X_test)
print("R2:", r2_score(y_test, pred_1))

# RF
model_2 = models[1]
model_2.fit(X_train, y_train)
pred_2 = model_2.predict(X_test)
print("R2:", r2_score(y_test, pred_2))

# ET
model_3 = models[2]
model_3.fit(X_train, y_train)
pred_3 = model_1.predict(X_test)
print("R2:", r2_score(y_test, pred_3))

# ADA
model_4 = models[3]
model_4.fit(X_train, y_train)
pred_4 = model_4.predict(X_test)
print("R2:", r2_score(y_test, pred_4))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

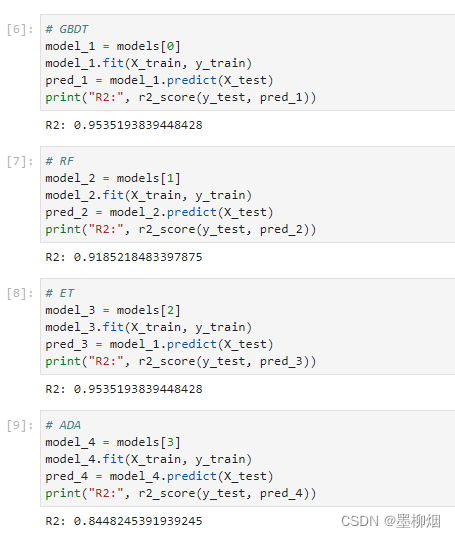
结论

最后得到的集成模型的学习结果显然要优于4个基模型。