人工智能知识全面讲解：线性支持向量机

经常喝咖啡的朋友知道，咖啡豆的产地不同，冲出来的咖啡口味也不相
同。阿拉比卡的咖啡具有均衡的风味、口感与香气，而罗布斯塔的咖啡带有强
烈的酸味，口感比较浓郁。挑选咖啡豆是一件非常有讲究的事情，如何区分两
种不同的咖啡豆呢？
假设我们现在要训练一个模型，借助计算机将两种不同产地的咖啡豆区分
开来。经过前面章节的学习，我们很自然会想到使用感知机算法。使用感知机
算法，只需要从已有咖啡豆的“豆体”和“颜色”这两个特征数据不断调整模
型，就能学习得到一个超平面将两类咖啡豆分开。我们也知道在感知机算法
中，赋予的初始值和参数不同，这个划分超平面的位置也不同，如图8-1所
示。图中两种颜色的数据点代表两种不同类别的咖啡豆，可以看到三个图中的
直线都能够将两个产地的咖啡豆分开，但是哪种分类效果最好呢？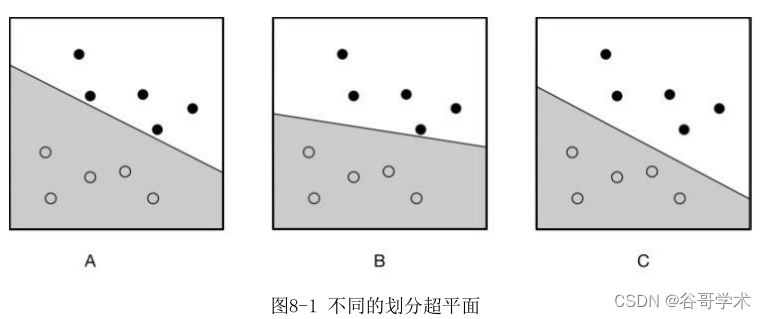

 分类效果最好的划分直线，一定对新来的咖啡豆能够准确划分。从图像上
看，新样本点距离哪边的样本点更接近，那么它属于那个类别的概率就会更
高。因此可以从距离的角度出发，定?分类效果最好的划分直线。如图8-2所
示，在决策面不变的情况?，我们添加一个新的咖啡豆。这时可以看到，分类
器 C 依然能有很好的分类结果，而分类器B则出现了分类错误。

也就是说，我们应该去找位于两类训练样本数据点“正中间”的划分直
线，因为这个划分直线对新数据的包容性最好。新的数据在平面内的分布是随
机的，因此总会出现比训练数据点更接近分界线的情况，这就导致许多划分直
线出现错误分类，而位于“正中间”的划分直线受影响最小，所以我们认为这
个划分直线的效果最好。用专业术语讲，我们说这个划分直线的“鲁棒性”最
好。鲁棒是 Robust 的音译，也就是健壮、强壮的意思。所谓鲁棒性我们可以
理解为稳定性，是指系统在一定参数调整的变化?，维持其他性能的特性。
8.1.2 支持向量来帮忙
为了描述这个“正中间”，我们引入“支持向量”（Support Vector）的
概念来表示这个间隔。在两个类别的分界面处总是可以找到各自的一些样本
点，以这些样本点的中垂线划分，可以使类别中的点都离分界面足够远，这个
分隔线所在的划分面就是最理想的分割超平面，如图8-3所示。而支持向量
机，其实就是找到这个超平面的方法。

 

支持向量机（Support Vector Machine，SVM）是丹麦科学家科琳娜
（Corinna Cortes）教授与俄罗斯统计学家万普尼克（Vladimir Naumovich
Vapnik）教授等于1995年提出的一种适用于二分类的机器学习算法。它的核心
思想是对于给定的数据集，在样本空间中找到一条划分直线，从而将两个不同
类别的样本分开，并且这条直线距离最接近的训练数据点最远。
虽然SVM的推导过程涉及公式较多，比较复杂，但这里仍然希望产品经理
能够理解推导的思路及关键步骤，这对深入理解分类算法有很大的帮助。本章
比较特殊，我们会花一些时间在公式的推导上，重点讲解SVM的推导过程。
8.2 线性支持向量机推导过程
8.2.1 SVM的数学定义
我们知道，SVM算法的目的是找到距离两类数据间隔最大的超平面 ，实
际上就是求解得到一个超平面：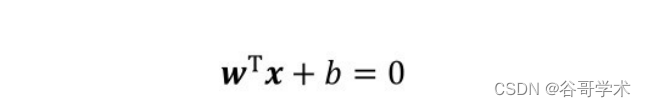

 

式中，w  T x 表示法向量，其决定了超平面的方向；b表示位移项，决定
了超平面与原点之间的距离。显而易见，求解SVM就是求解式中的参数w 和b，
确定了这两个参数就能确定这个超平面的位置。如何求解w 和b？怎么判断训
练后的参数w 、 b构成的平面已经足够好呢？
解决这个问题的唯一方法是将它转换成数学问题，从而明确求解的目标以
及约束条件。如果转化成数学问题，我们需要构建对应的函数来表达划分超平
面。要构建函数，我们很自然能想到从距离入手，通过距离计算哪个是间隔最
大的超平面 。因此我们要定?距离，根据点到平面的距离公式和超平面公
式， 推导得到几何间隔为

 

 

式中，y i =+1表示样本为正样本，y i =−1表示样本为负样本。这里设置大
于等于1以及小于等于-1 只是为了计算方便，原则上可以取任意常数。但无论
正负样本取值如何，都可以通过对w的变换使其转化为1和-1，此时将上式?右
都乘以y i ，得到

 

 

至此，我们求出了样本点到划分平面之间的间隔的表达式为 

式中，m为样本点的总个数。上述公式描述的是一个典型的在不等式约束
条件?的二次型函数优化问题，同时也是支持向量机的基本数学模型。
至此，我们的第一个任务完成了。第一环节我们所做的事情是将寻找最优
的分割超平面的问题转换为带有一系列不等式约束的优化问题，这个优化问题
被称作原问题。直接对原问题进行求解比较复杂，我们需要找到一个更高效的
方法来求解，目前常用的方法为拉格朗日乘子法。
8.2.2 拉格朗日乘子法
我们的目的是求解支持向量机的最小间隔，也就是求解原问题的最小值。
但是我们目前遇到的问题是原问题有约束的优化问题，不容易求解。所以最直
观的解决方法是构造一个函数，使得该函数在可行解区域内与原目标函数完全
一致，而若在可行解区域外的数值非常大，甚至是无穷大，那么这个没有约束
条件的新目标函数的优化问题就与原来有约束条件的原始目标函数的优化问题
是等价的问题。这就是使用拉格朗日方程的目的，它将约束条件放到目标函数
中，从而将有约束的优化问题转换为无约束的优化问题。
具体来说，就是对原问题的每条约束条件添加拉格朗日乘子α i ≥0，则
该问题的拉格朗日函数可写为 

转换的初衷是为了建立一个在可行解区域内与原目标函数相同，在可行解
区域外函数值趋近于无穷大的新函数。现在，我们的问题变成了求新目标函数
的最小值，即：

 

我们需要先求新目标函数的最大值，再求最小值。这样一来，首先需要求
解带有参数w 和b的方程，而α i 又是不等式约束，所以不容易求解。因此需
要将问题再进行一次转换，以便更容易求解。在这里，我们采用一个数学技
巧：拉格朗日对偶。通过拉格朗日对偶将求解某一类最优化（如最小化）问题
转换为求解另一种最优化（如最大化）问题，这样做的好处是使得问题的求解
更容易。所以，我们需要使用拉格朗日函数的对偶性，将最小和最大的位置交
换一?，上面的式子变为：

 

转换以后得到的新式子是原始问题的对偶问题，这个新问题的最优值用d ∗
来表示。而且新式子与原式子的关系是d ∗ ≤P * 。在这个式子中，我们关心的
是在什么情况?d=p，这才是我们需要的最终解。要让d=p，必须满足两个条
件：
（1）这个优化问题必须是凸优化问题。
（2）这个问题需要满足KKT条件。
接?来我们简单介绍一?这两个条件。
1. 凸函数
我们先解释什么是凸函数。要理解凸函数，我们需要理解凸集这个概念。
凸集（convex set）是在凸组合?闭合的放射空间的子集。如图8-5所示，A、
B都是一个集合。如果集合中任意2个元素连线上的点也在集合中，那么这个集
合就是凸集。从图中可以看出来，图8.5的?图是一个凸集，右图是一个非凸
集。

 

凸函数的定?也是如此，其几何意?为，函数任意两点连线上的值大于对
应自变量处的函数值。从数学定?上讲，对区间[a，b]上定?的函数 ?，若它
对区间中任意两点均满足：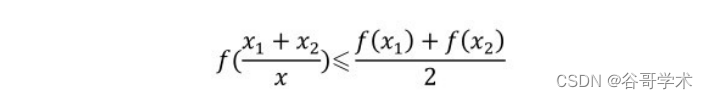

 

则该函数为凸函数。根据这个定?，我们的目标函数显然是一个凸函数。
2. 不等式约束的最优化问题
实际上，求解最优化问题就是求解函数的最大值或最小值。很多读者对求
解最优问题并不陌生，因为在高中数学课上我们已经学习过如何求解一个函数
的最大值或最小值。举个简单的例子，已知函数y=x 2 ，求y的最小值。一般的
做法是先对函数求导，然后令导数为 0，就可以得到极小值点对应的x值，代
入原函数后得到对应的极小值y，此处的极小值就是最小值。所以求解函数最
小值的方式是求导，令原函数导数为0。现在我们需要求解的最优化问题，因
为带有不等式约束条件，也就是说需要在满足不等式的条件?，求解最大或最
小值，这比没有约束条件时更复杂。
解决这类带有不等式约束的最优化问题，通常使用“KKT条件”。该方法
是将原函数所有的约束条件与原函数 ?(x)统一列为拉格朗日函数。以拉格朗
日乘子为系数，通过特定的条件，得到求出最优值的必要条件。这个条件称为
KKT条件。
8.2.3 对偶问题求解
显然，我们的待求解问题是凸函数，并且在数学上可证明待求解问题也满
足KKT条件（在此我们省略了原问题满足KKT条件的推导）。符合以上两个条件
后，我们可以将原问题转换为“对偶问题”。

 

 

8.2.4 SMO算法
1996年，约翰·普拉特（John Platt）教授发现了一个使用“最小序列优
化”法训练SVM的算法，称为SMO（Sequential Minimal Optimizaion）算法。
SMO算法的核心思想与动态规划相似，是一种启发式算法。它将一个大优化问
题分解为多个小优化问题来求解，这些小优化问题通常很容易求解，并且对它
们进行顺序求解的结果与将它们作为整体求解的结果完全一致。使用SMO算法
的好处在于求解时间较短。
SMO算法的工作原理是：在每次循环中选择两个α进行优化处理，一旦找
到了一对合适的α，那么就增大其中一个同时减小另一个。这里所谓的“合
适”就是指两个 α 必须符合以?两个条件：其一是两个 α 必须在间隔边界
之外；其二是这两个 α还没有被进行过区间化处理或者不在边界上。
SMO算法的求解步骤为：
（1）选择一对需要更新的变量α i 、α j 。
（2）固定除了这两个变量外的其他所有变量（即看作常量），将问题简
化。
（3）求解简化后的问题，并更新α i 、α j 。
（4）重复前三个步骤，直到收敛。
在此我们省略了SMO算法求解极小化问题的过程，直接得到w 、b的取值为

 

至此，我们求出了SVM的终极表达式。在实际应用时，根据KKT条件中的对
偶问题互补条件，如果 α i >0，则原式=1，表示样本点在支持向量上；如果
α i =0，则原式≥1，表示样本点在支持向量上或者已经被正确分类。
总结SVM求解的全过程，可分为以?几个步骤：
（1）通过“支持向量”求出超平面的表达式。
（2）构造约束优化条件。
（3）将有约束的原始目标函数转换为无约束的新构造的拉格朗日目标函
数。
（4）利用拉格朗日对偶性，将不易求解的优化问题转化为易求解的优化
问题。
（5）利用SMO方法求解。
至此，我们完整地学习了SVM的数学推导步骤。推导过程并不难理解，主
要是涉及的数学概念较多，转换过程以及证明过程比较烦琐，导致很多读者望
而生畏。同时，体会这个推导过程也能让我们感受到数学对于人工智能发展的
重要性。将一个实际问题形式化，建立数学模型求解，从数学上找到解决问题
的途径，从而解决更多的业务问题。