-
C++实现排序 - 02 归并排序、快速排序和堆排序
写在前面:
今天我们继续来整理平均时间复杂度为 O(nlogn) 的三个排序算法,即归并排序、堆排序和快速排序。排序算法 平均时间复杂度 最好情况 最坏情况 空间复杂度 稳定性 归并排序 O(nlogn) O(nlogn) O(nlogn) O(n) 稳定 快速排序 O(nlogn) O(nlogn) O(n2) O(nlogn) 不稳定 堆排序 O(nlogn) O(nlogn) O(nlogn) O(1) 不稳定 归并排序
归并排序采用了分治法的思想,不断将两个有序的序列进行合并从而最终得到整个有序的序列,算法步骤如下:
- 把当前长度为 n 的序列分为两个长度为 n / 2 的子序列,对子序列进行操作。
- 同样对两个子序列进行划分,再分别对其子序列进行划分操作,直至子序列中只有一个元素为止就不再进行划分,而是进行回溯。
- 通过回溯的子序列进行排序操作,我们额外创建一个数组出来,将回溯的两个子序列进行合并操作。
- 一直往上回溯,这样每次得到的两个回溯的子序列都是有序的,可以方便我们进行合并操作,合并的序列也会是有序的。
直接上图:
我们先对序列进行划分操作:
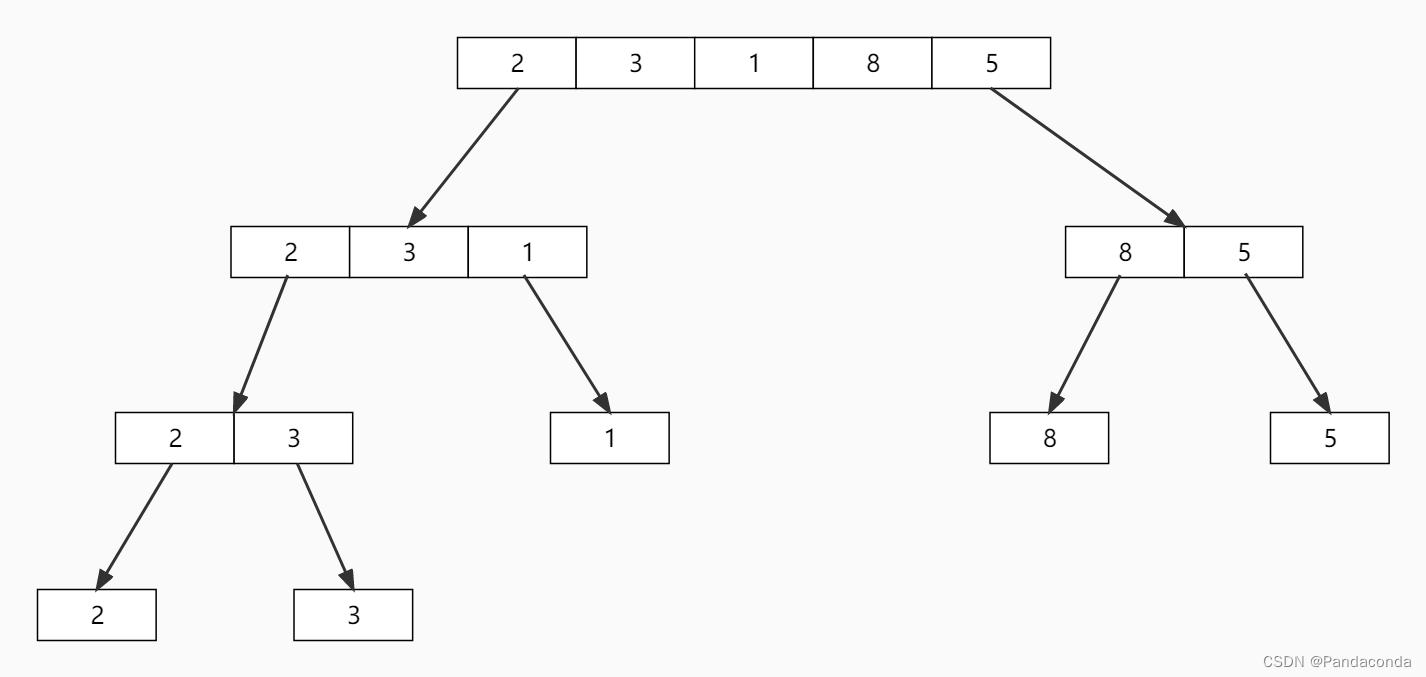
然后对各个子序列进行回溯:
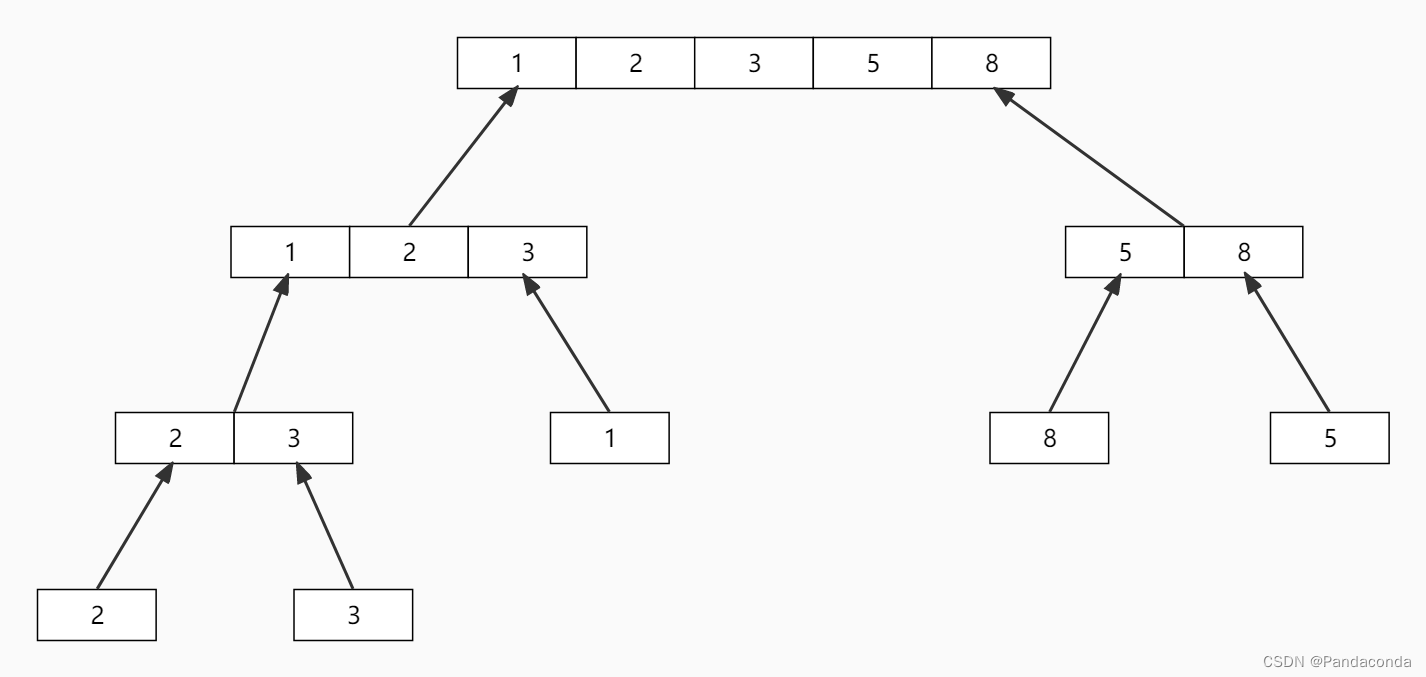
通过合并操作,得到最终的子序列。
#include <bits/stdc++.h> using namespace std; int n, q[100010], temp[100010]; void merge_sort(int q[], int l, int r) { //如果当前序列只有一个元素,则不用排序直接返回 if (l >= r) return; //对序列进行划分,然后对其子序列进行递归操作 int mid = l + r >> 1; merge_sort(q, l, mid), merge_sort(q, mid + 1, r); //合并操作 int k = 0, i = l, j = mid + 1; while (i <= mid && j <= r) { //遍历两个子序列,将更小的元素取出放入临时数组temp if (q[i] <= q[j]) temp[k++] = q[i++]; else temp[k++] = q[j++]; } //如果还有元素没有取出,将剩余元素放入临时数组temp while (i <= mid) temp[k++] = q[i++]; while (j <= r) temp[k++] = q[j++]; //将原数组进行更新,更新上面合并的区间 for (int i = l, j = 0; i <= r; i++, j++) q[i] = temp[j]; } int main() { /* 5 2 3 1 8 5 */ scanf("%d", &n); for (int i = 0; i < n; i++) { scanf("%d", &q[i]); } merge_sort(q, 0, n - 1); for (int i = 0; i < n; i++) { printf("%d ", q[i]); } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
快速排序
快速排序也是利用了递归思想,算法步骤如下:
- 选取第一个的数作为基准数。
- 将小于基准数的元素换到前面,将大于基准数的元素换到后面。
- 重复上述操作,直到区间只有一个数为止。
直接上图:
第一步:选取第一个数作为基准数。
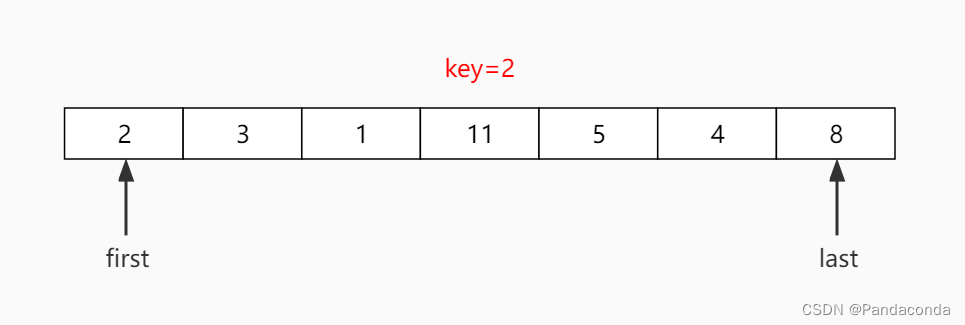
第二步:从后往前找一个比基准数小的数放到前面。
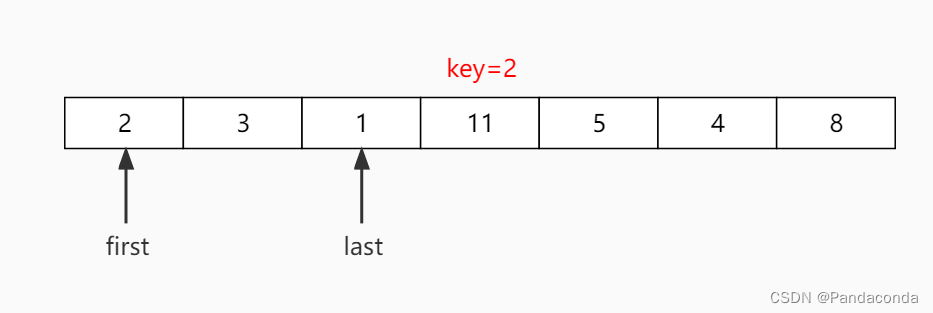
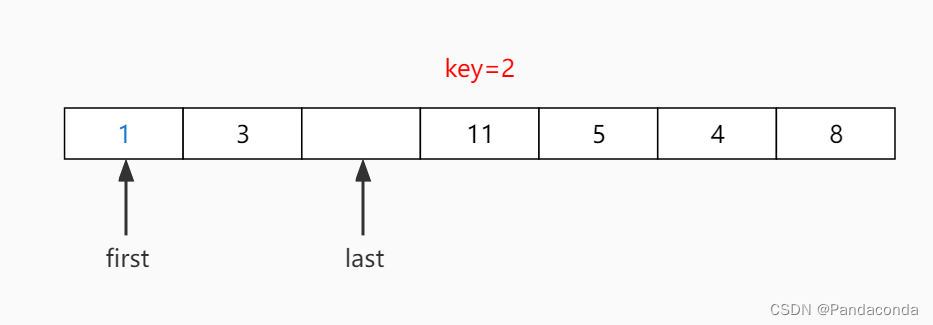
第三步:从前往后找到一个比基准数大的树放到后面。
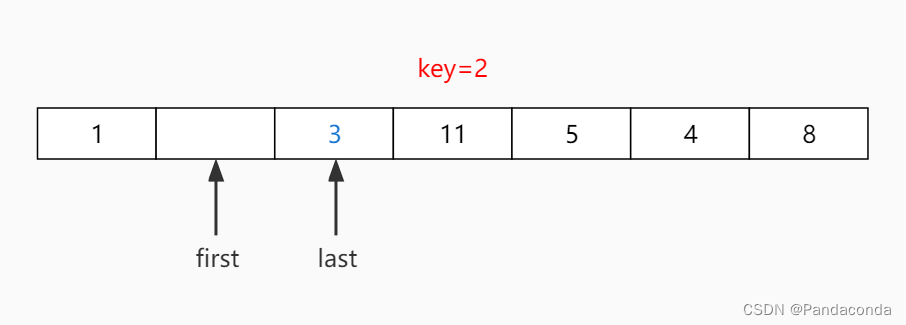
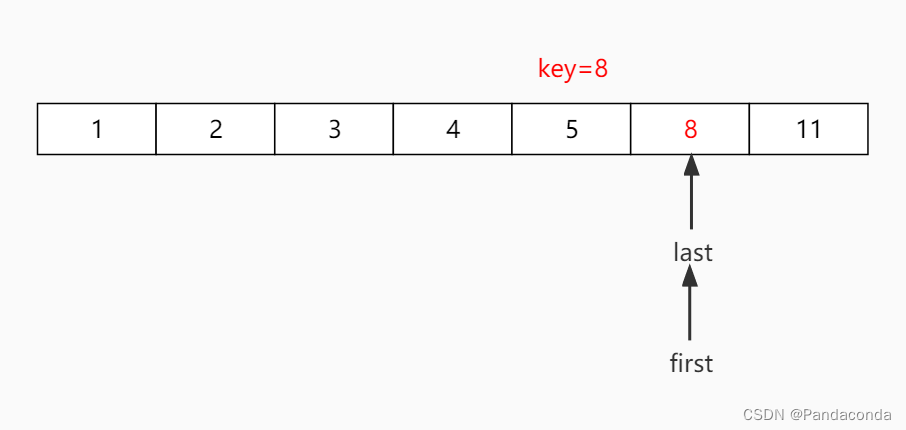
第四步:继续从后往前查找,发现 first 和 last 重合,本次遍历结束,并将基准数放到指针所指地方。
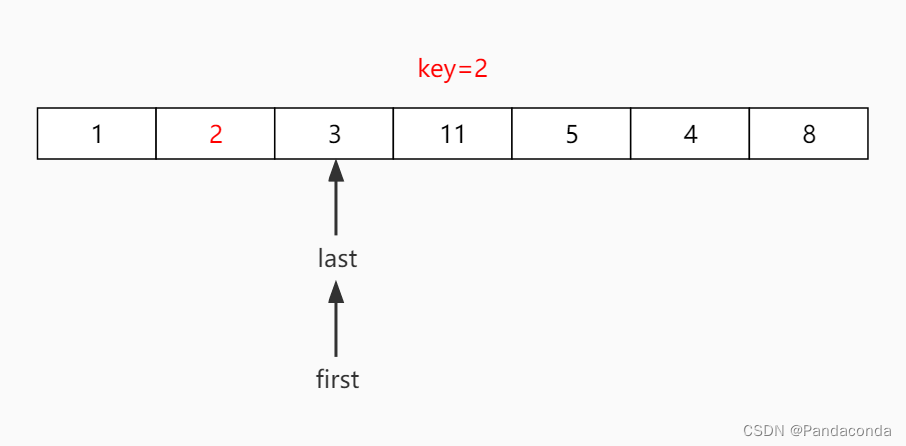
第五步:将该序列分成两半,左半部分是该序列左边界至 first -1 ,右半部分是 first +1 至右边界。
第六步:对左半部分即下标为 0 ~ 1 区间进行递归排序,由于已经是有序我们就直接跳过这里。
第七步:对右半部分即下标为 3 ~ 6 区间进行递归排序。
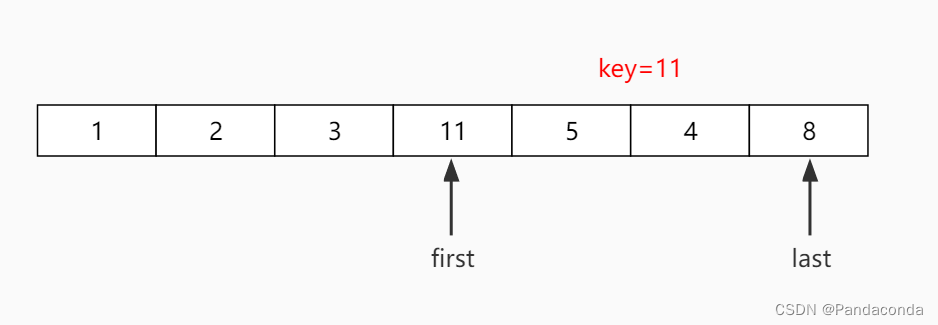
第八步:从后往前找到一个比基准数小的数放到前面。
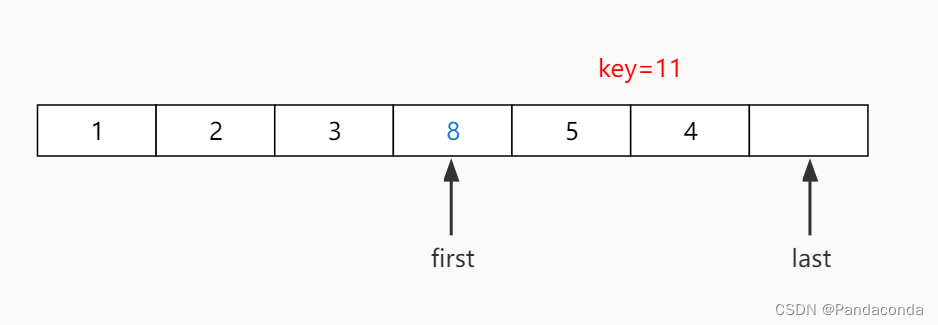
第九步:从前往后找一个比基准数大的数放到后面,但是发现指针最终重合,故此次遍历结束,将基准数放到指针所指位置。
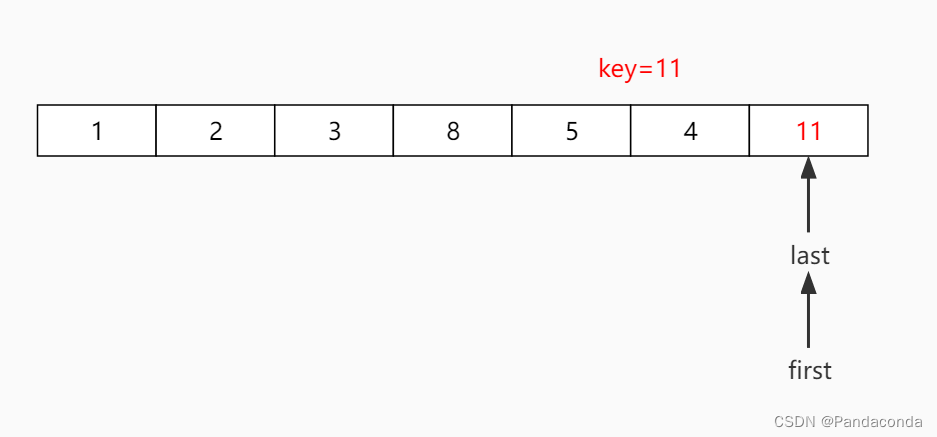
第十步:与上面相同,对该序列进行左右区间划分,再分别遍历。由于右半部分已经没有元素了,我们直接对左半部分即下标为 3 ~ 5 区间进行递归排序。
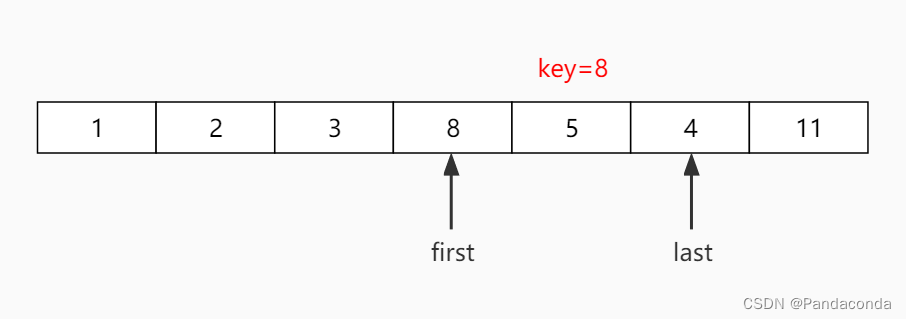
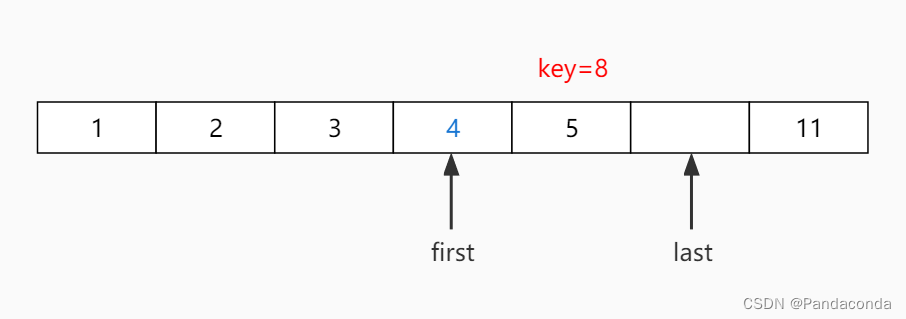
由于该序列已经有序,后续递归操作我们就不再展示了,直接来看代码。
#include <bits/stdc++.h> using namespace std; int q[1000010]; void quick_sort(int q[], int l, int r) { if (l >= r) return; int first = l, last = r, key = q[first]; while (first < last) { //将比第一个小的移到前面 while (first < last && q[last] >= key) last--; if (first < last) q[first++] = q[last]; //将比第一个大的数移到后面 while (first < last && q[first] <= key) first++; if (first < last) q[last--] = q[first]; } q[first] = key; quick_sort(q, l, first - 1), quick_sort(q, first + 1, r); } int main() { /* 7 2 3 1 8 5 11 4 */ int size = 0; scanf("%d", &size); for (int i = 0; i < size; i++) { scanf("%d", &q[i]); } quick_sort(q, 0, size - 1); for (int i = 0; i < size; i++) { printf("%d ", q[i]); } return 0; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
堆排序
在了解堆排序之前,我们先来看看什么是堆。
堆就是一个类似于完全二叉树的结构,同时它分为大顶堆和小顶堆,它们的性质分别是每个结点的值都大于(或小于)它的孩子结点。
下面就是一个大顶堆:
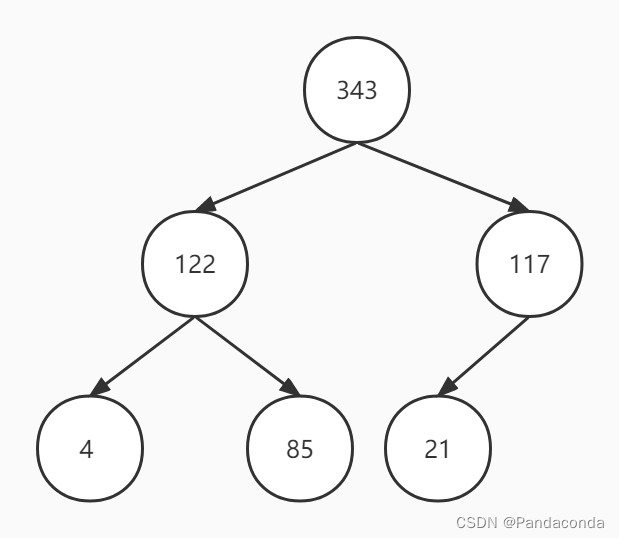
下面就是一个小顶堆:
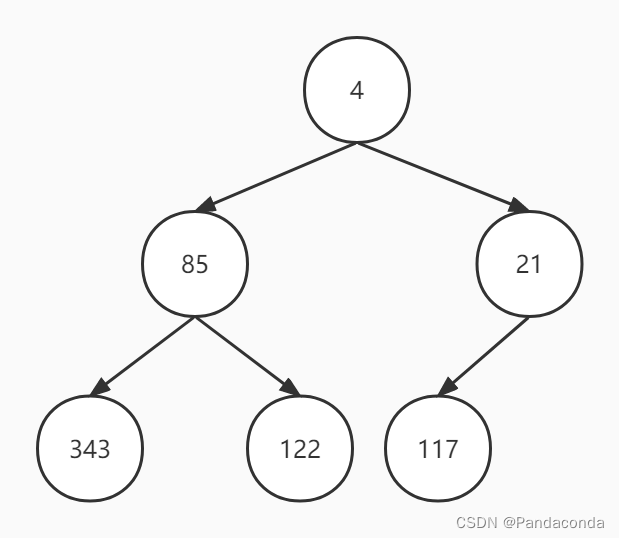
那么我们如何利用堆的性质进行排序呢,算法步骤如下(这里讲解升序操作):
- 先将初始化的数组序列构建成大顶堆。
- 将堆顶元素和最后一个元素进行交换,此时最后一个元素的位置就是该序列的最大值了。然后再对其前面的所有元素进行堆更新,即从堆顶元素往下进行堆操作,但是这里已经排好序的最后一个元素不参与对操作。
- 重复上述步骤,每次都从堆顶取剩余元素的最大值放到堆即剩余元素的最后一个,然后从堆顶往下进行对操作,直至所有元素都已经操作完。
可能会有小伙伴比较有疑惑,我们该如何确定已经排好序和没有排好序的元素呢。这就需要用到完全二叉树的性质:
在下标从 0 开始存储元素的顺序存储的数组当中,结点的左孩子下标等于该结点下标乘以 2 加 1 ,结点的右孩子下标等于该结点下标乘以 2 加 2 。
这样我们可以通过数组下标进行操作,先对前 n 个元素构建大顶堆。然后交换堆顶和最后一个元素,确定数组中第 n 个元素的序列,再对前 n - 1 个元素进行堆操作。
直接上图:
先来看看如何构建出大顶堆,我们要从第一个非叶子结点开始往上构建。因为如果从第一个结点开始往下构建的话,可能无法将最大的元素放到堆顶。
假设我们初始的序列为 { 21 , 343 , 122 , 84 , 5 , 117 , 4 } ,从第一个非叶子结点开始往上构建。
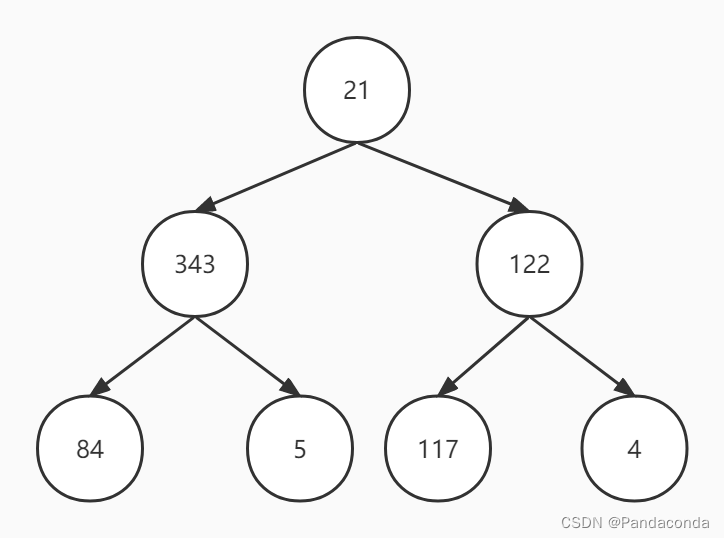
第一步:第一个非叶子结点为 122 ,每次都去找到该结点与其孩子结点中的最大值并进行交换,发现自身印记是最大值了,故找到上一个非叶子结点。
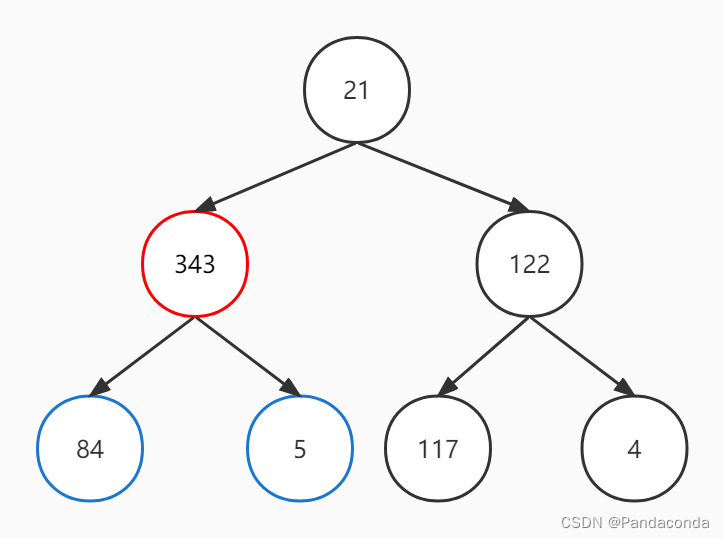
第二步:非叶子结点 122 已经是其和其孩子结点中的最大值,故不用交换。
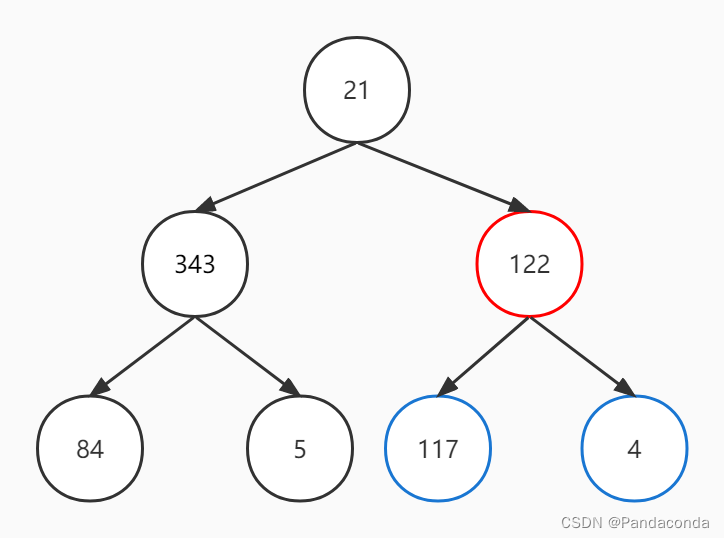
第三步:非叶子结点 21 与其孩子结点进行比较,发现其孩子结点 343 更大,故进行交换。
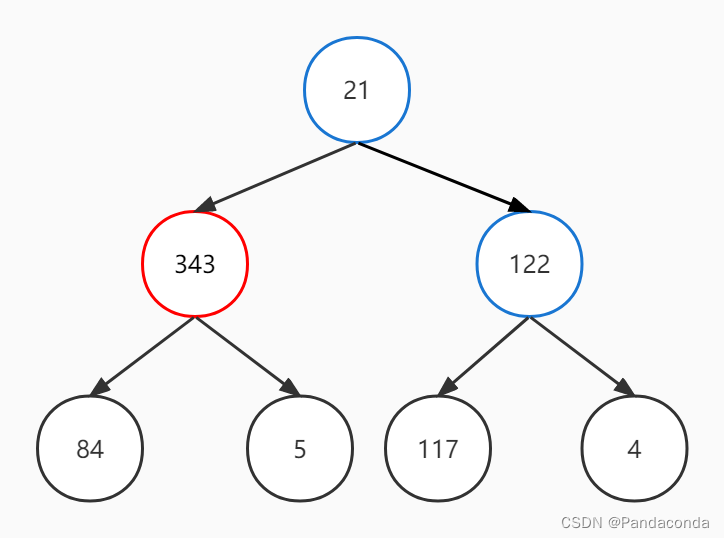
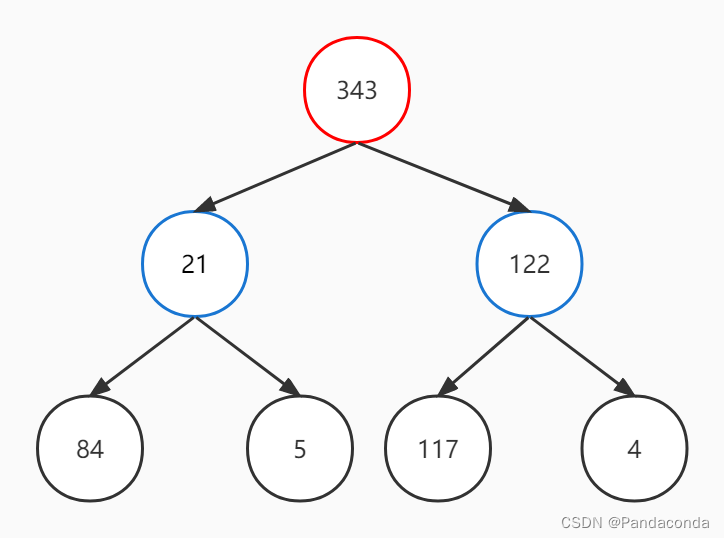
第四步:交换后的结点不是叶子结点,故继续向下找到最大值。
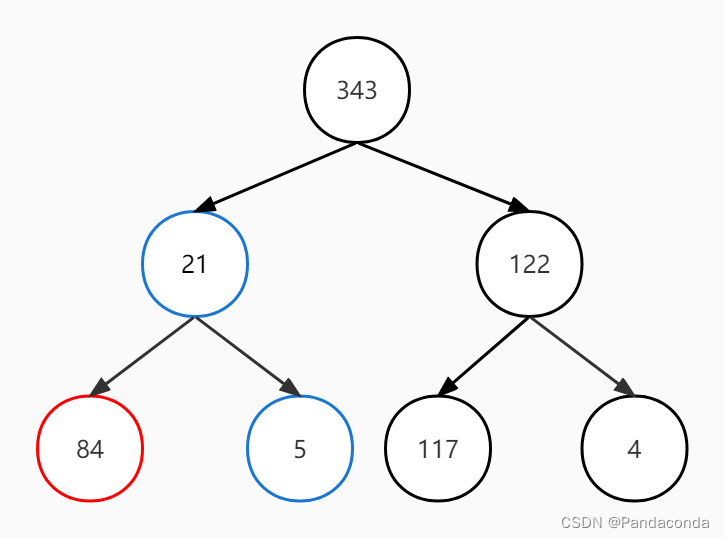
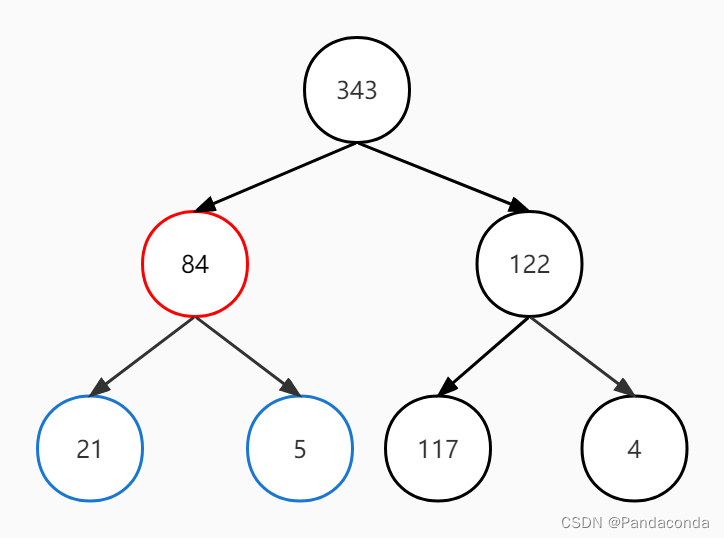
至此,大顶堆已经构建完成,现在进行排序操作。
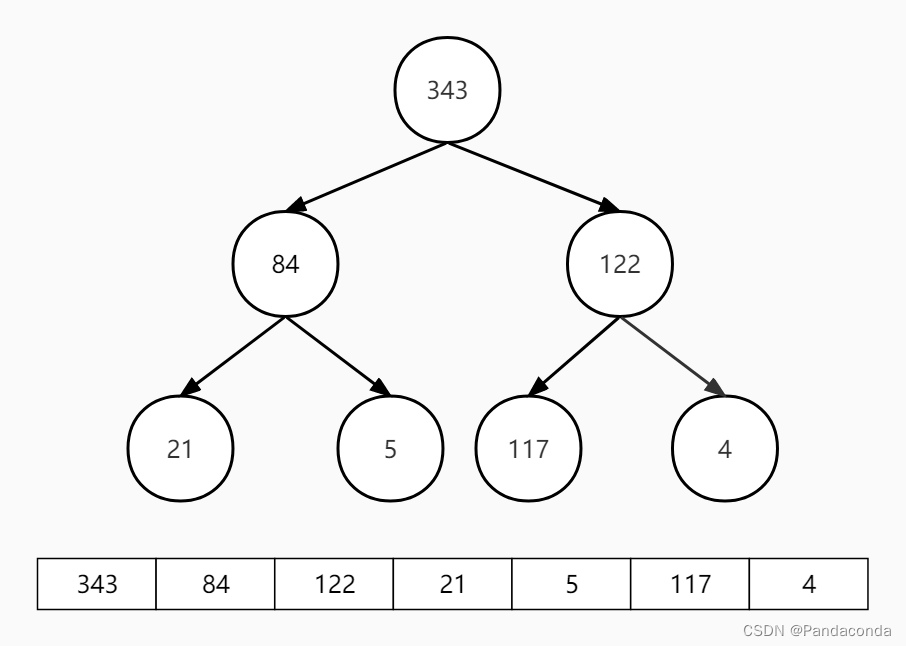
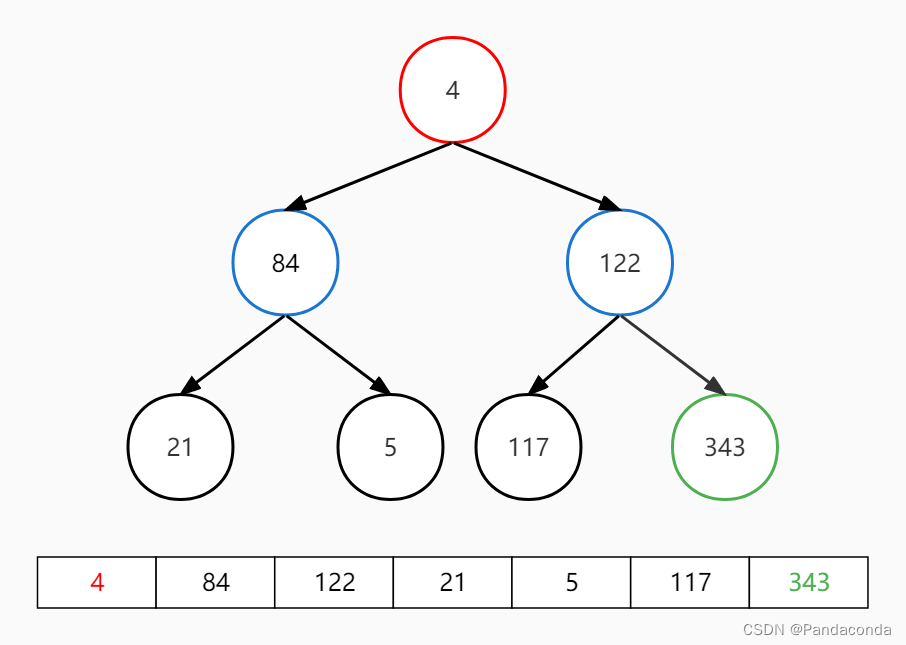
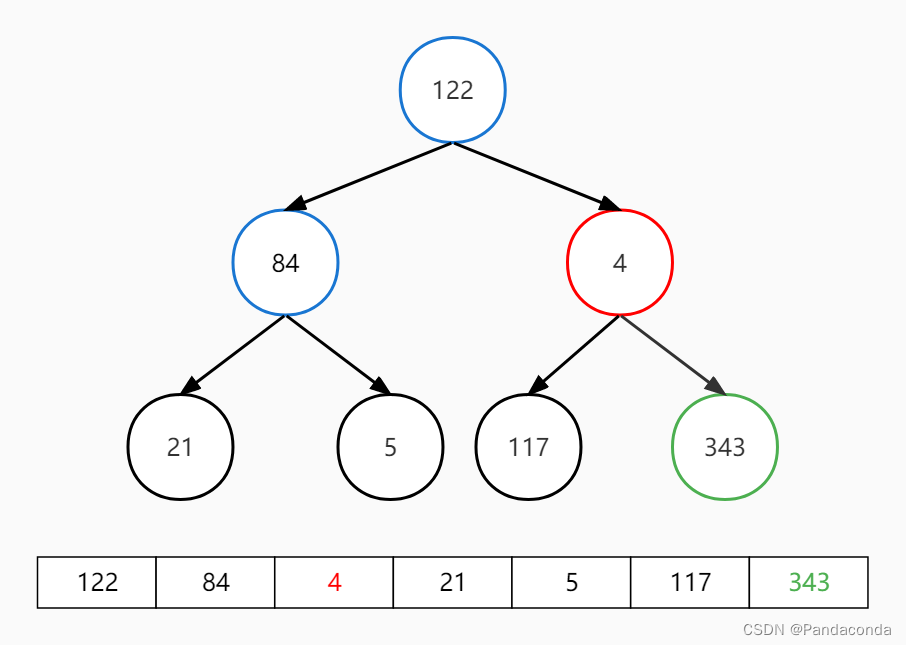
第一步:交换堆顶和最后一个元素。
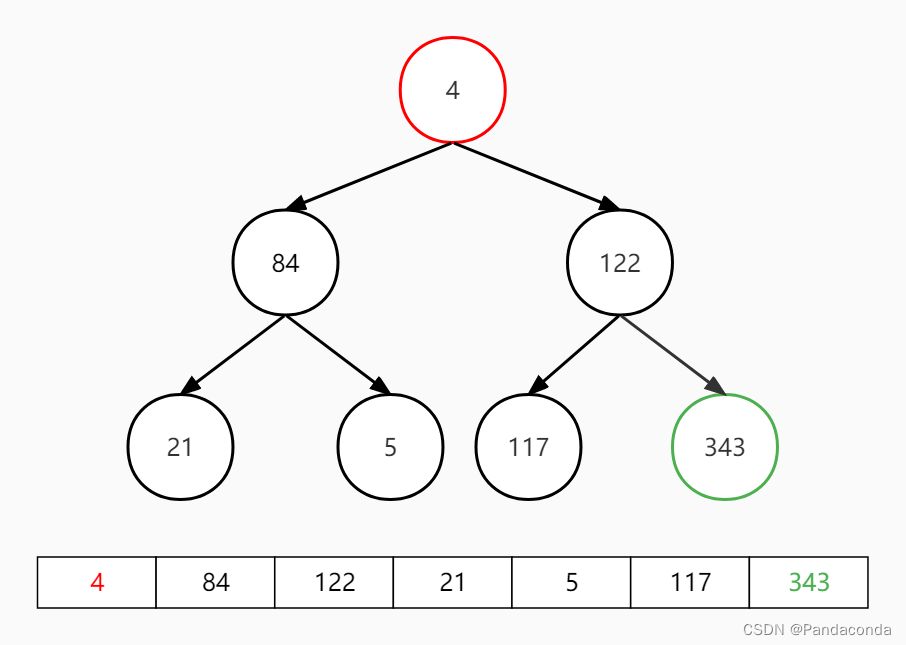
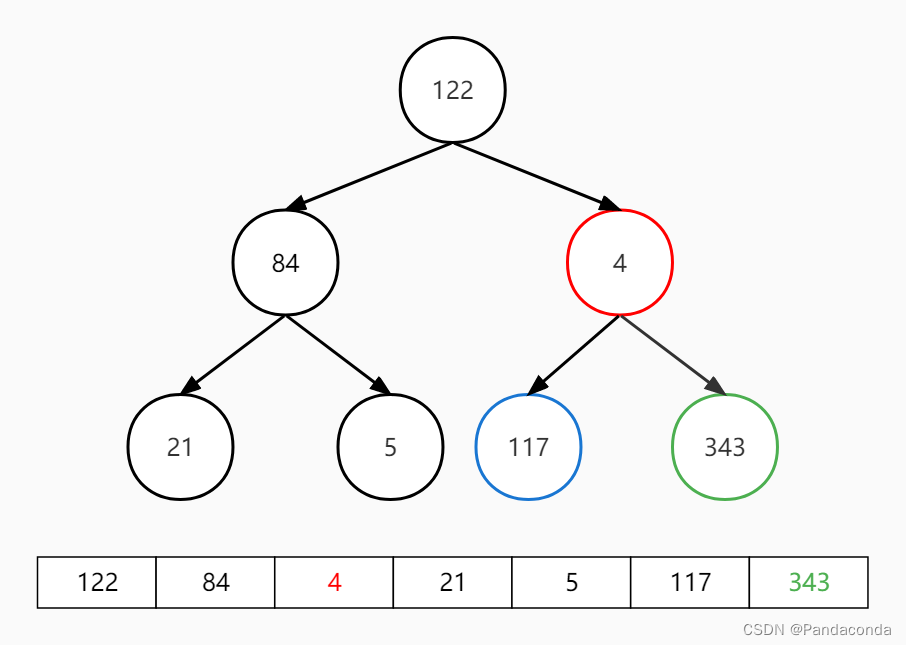
第二步:对堆顶元素向下进行对操作,注意已经排好序的 343 不再参与到对操作之中。
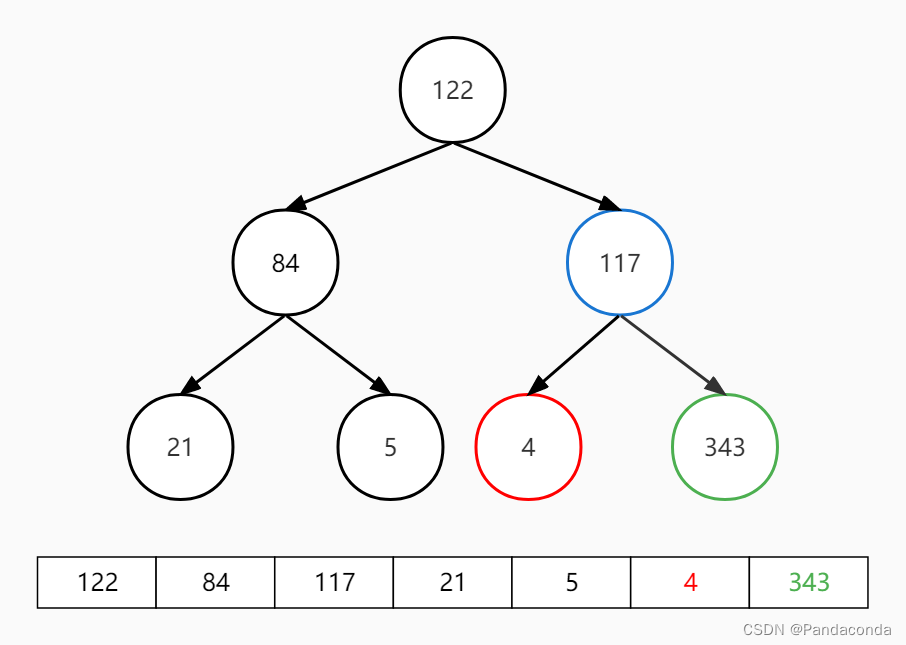
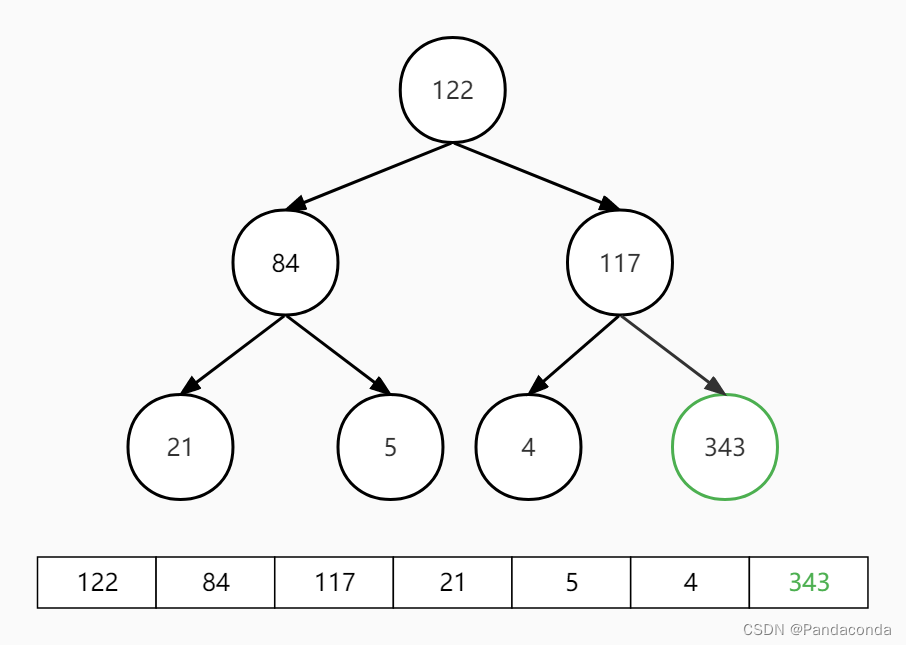
第三步:交换堆顶和最后一个元素,并对堆顶元素向下进行堆操作。
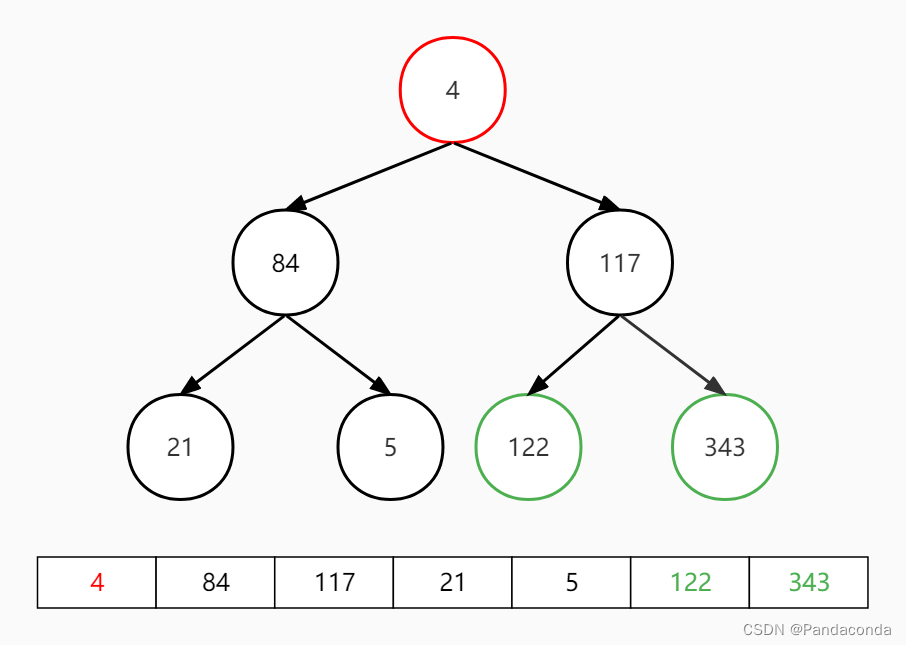
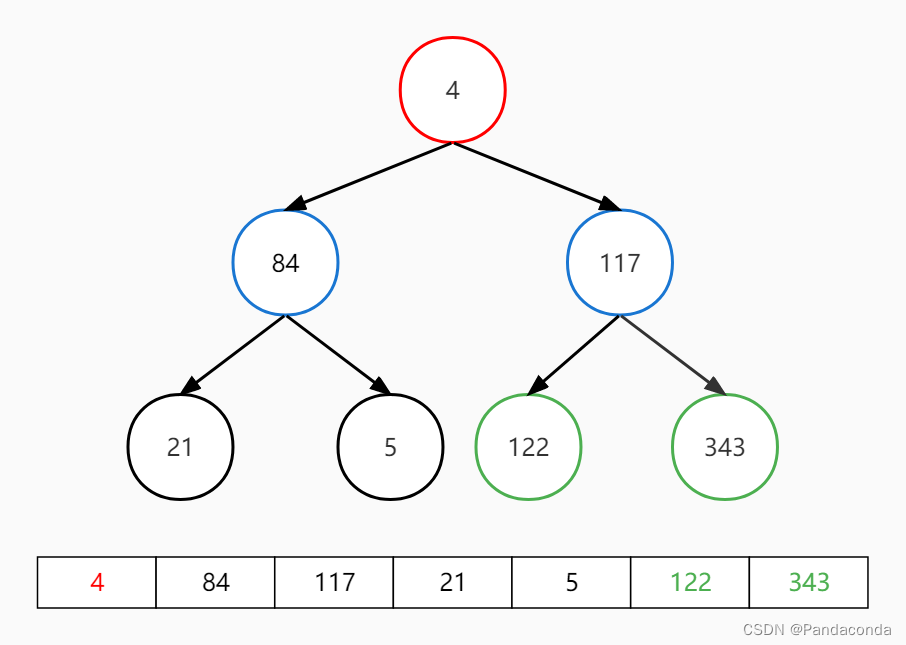
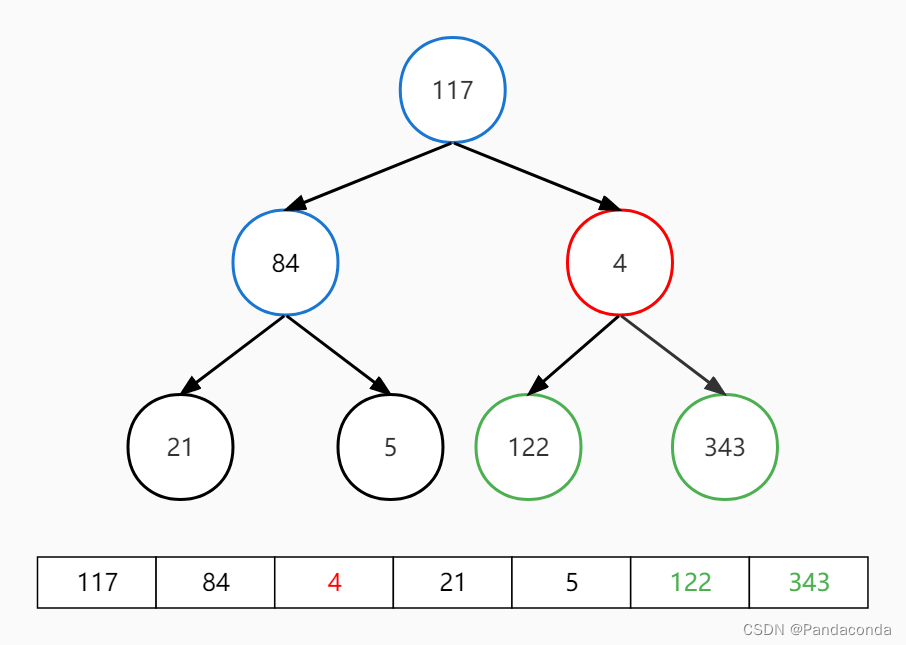
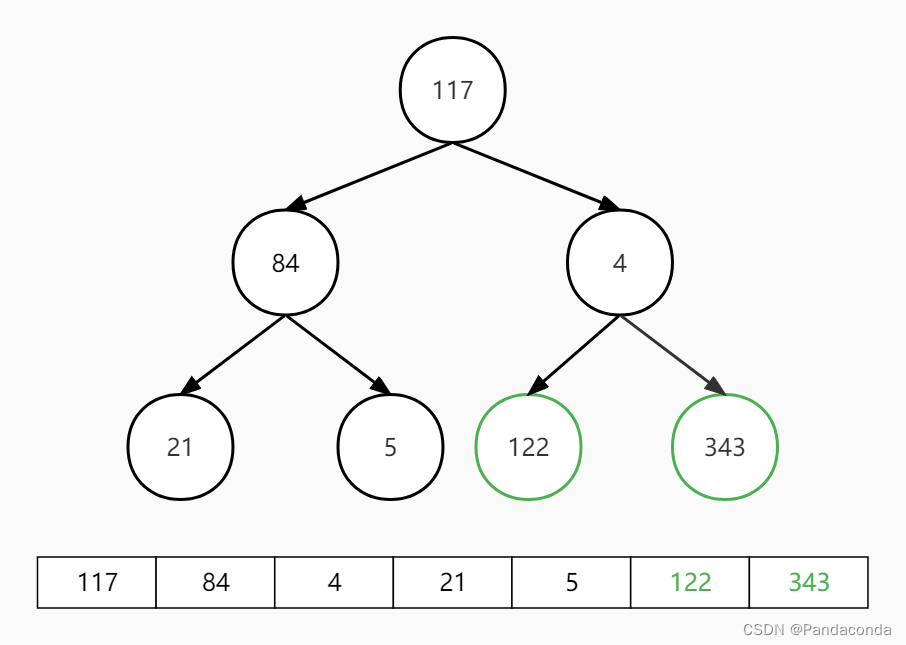
第四步:交换堆顶和最后一个元素,并对堆顶元素向下进行堆操作。
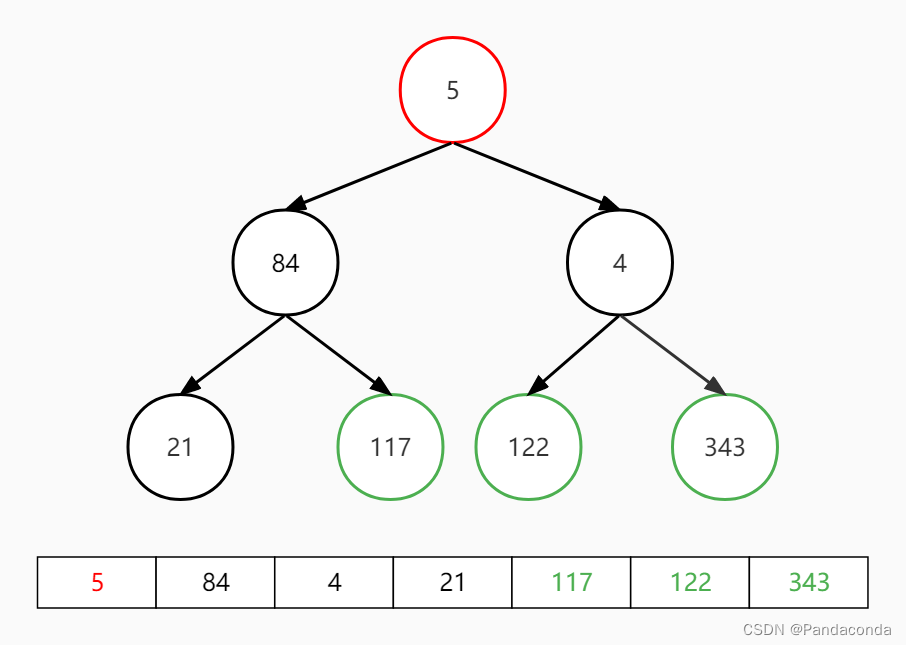
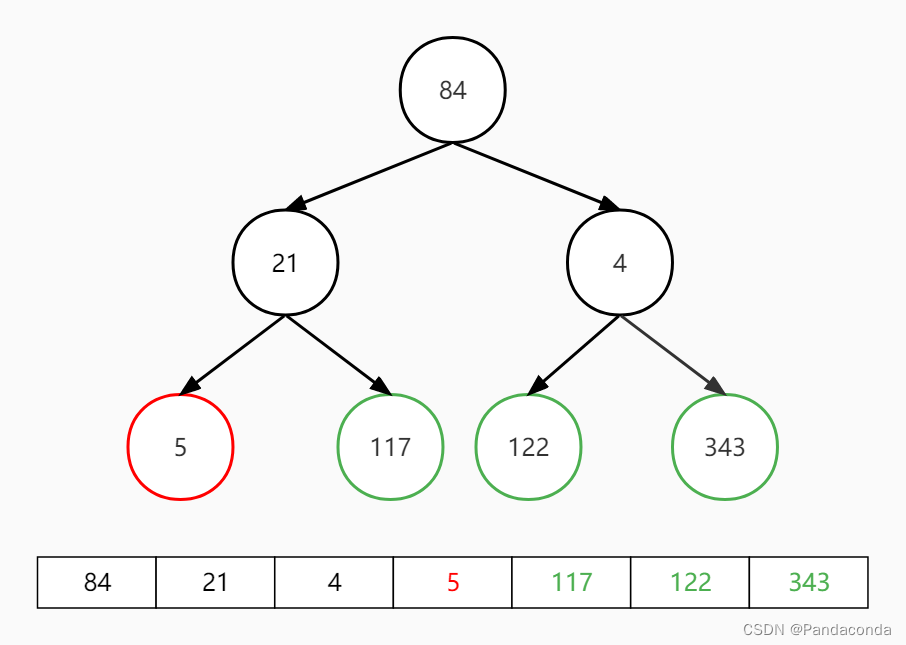
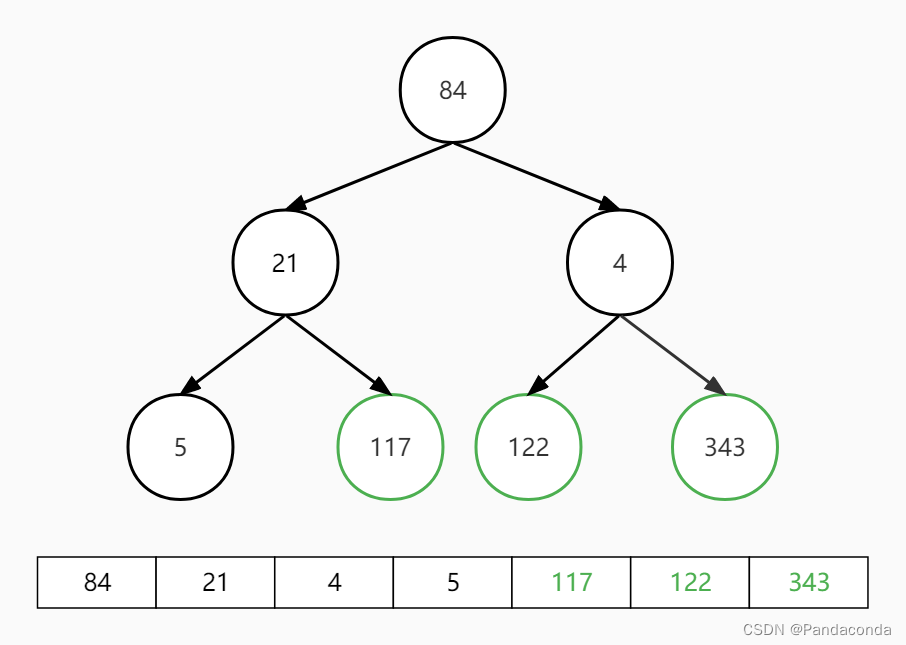
第五步:交换堆顶和最后一个元素,并对堆顶元素向下进行堆操作。
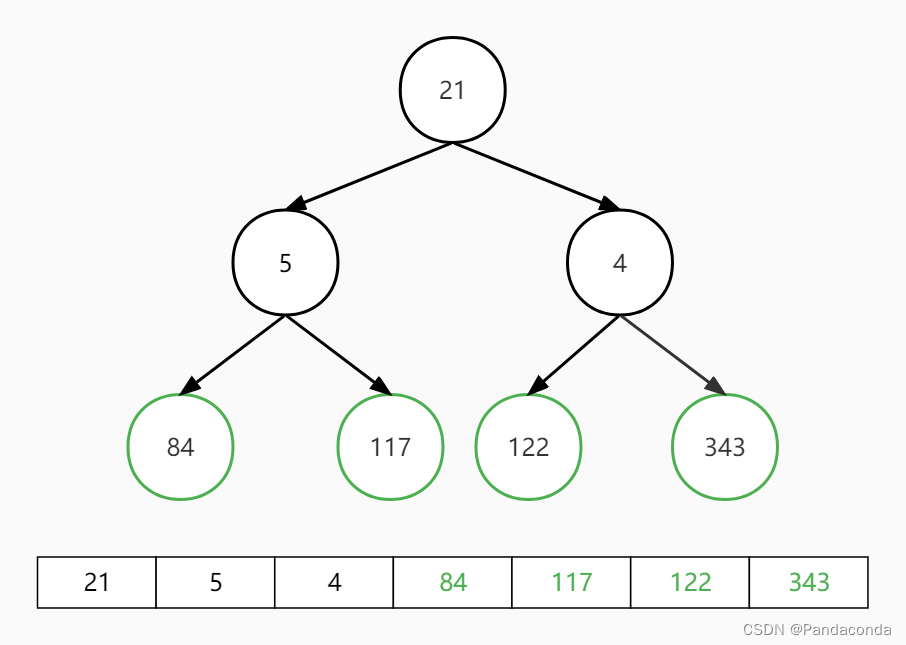
第六步:交换堆顶和最后一个元素,并对堆顶元素向下进行堆操作。
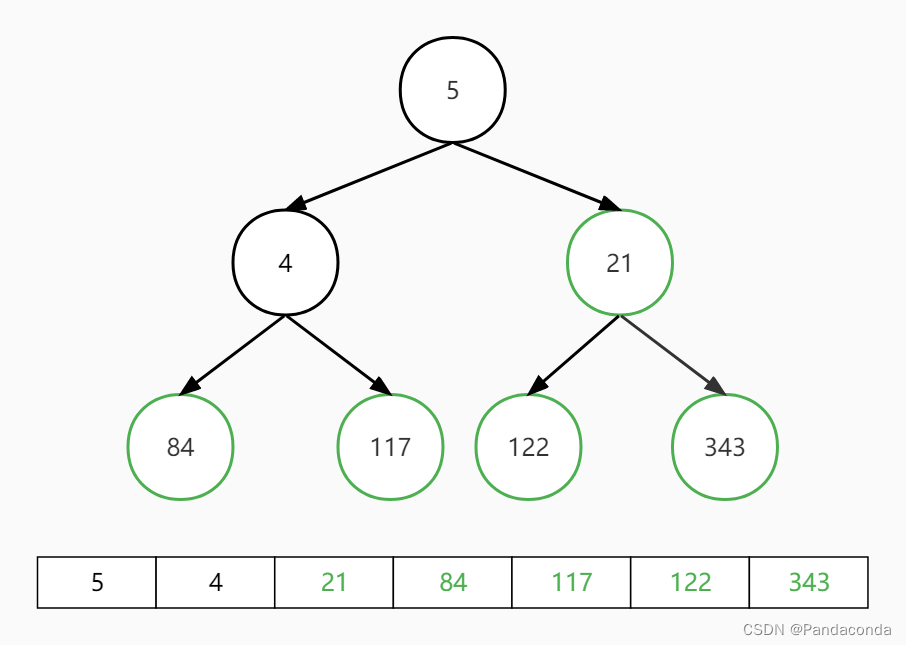
第七步:交换堆顶和最后一个元素,并对堆顶元素向下进行堆操作。
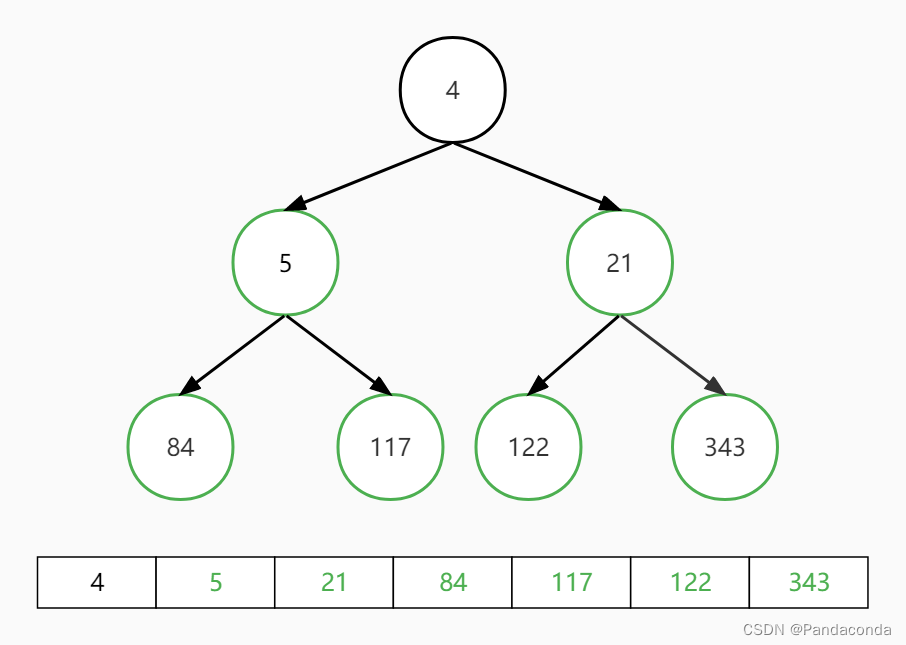
第八步:交换堆顶和最后一个元素,并对堆顶元素向下进行堆操作。
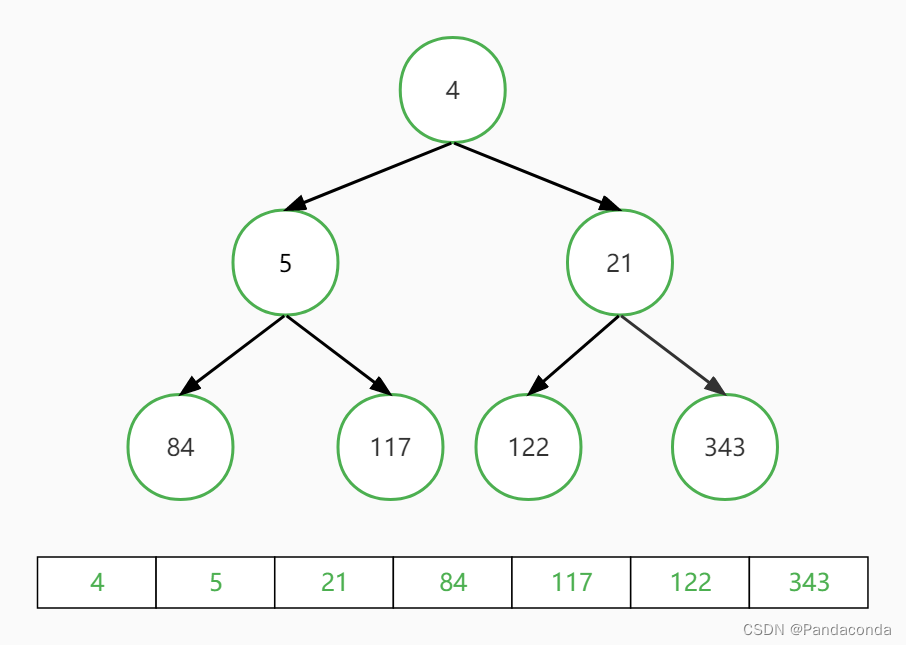
至此,所有元素都排好序了,直接输出即可。
#include <bits/stdc++.h> using namespace std; //用递归方式来调整为大顶堆 void adjust(int a[], int len, int index) { int right = index * 2 + 1; //index的右结点 int left = index * 2 + 2; //index的左结点 //找到三个结点中最大的一个,使其在index位置上 int maxIdx = index; if (right < len && a[right] > a[maxIdx]) maxIdx = right; if (left < len && a[left] > a[maxIdx]) maxIdx = left; if (maxIdx != index) { swap(a[maxIdx], a[index]); adjust(a, len, maxIdx); //变换结点后如果还有子结点,则继续进行排序 } } //堆排序 void heapSort(int a[], int size) { //从最后一个非叶子结点开始构建大顶推 for (int i = size / 2 - 1; i >= 0; i--) { adjust(a, size, i); } for (int i = size - 1; i > 0; i--) { swap(a[i], a[0]); //将大顶堆的根结点与最后一个结点交换,就得到了最大值 adjust(a, i, 0); //交换完后,继续对除交换到最后的元素之外的前面所有元素进行堆排序 } } int main() { int a[10] = { 21, 343, 122, 84, 5, 117, 4, 35, 90, 666 }; int size = 10; heapSort(a, size); for (int i = 0; i < size; i++) { cout << a[i] << " "; } return 0; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
如果大家有什么问题的话,欢迎在下方评论区进行讨论哦~
-
相关阅读:
Win7纯净版系统镜像64位介绍
C++求解一元一次方程——LeetCode 640
搭建自己的pypi服务器
SDUT PTA 栈和队列
图书目录管理系统(C++)
查找算法——二分查找法
哈夫曼树及其应用
四非到保研厦大,我们还有多少路要走----技术人的保研之路
三十八篇:架构大师之路:探索软件设计的无限可能
Amazon Linux 2022 来袭,AWS 承诺后续每两年更新一次
- 原文地址:https://blog.csdn.net/Newin2020/article/details/125497952
