机器学习笔记 - 时间序列使用机器学习进行预测

一、概述

        在最基本的情况下，我们将预测视为一个简单的回归问题，所有特征都来自单个输入，即时间索引。 只需生成想要的趋势和季节性特征，我们就可以轻松地创建未来任何时间的预测。

        然后，当我们添加滞后功能时，问题的性质发生了变化。 滞后特征要求在预测时已知滞后目标值。 滞后 1 功能将时间序列向前移动 1 步，这意味着您可以预测未来 1 步，但不能预测 2 步。接下来我们只是假设我们总是可以产生延迟到我们想要预测的时期（换句话说，每个预测都只是向前迈出一步）。现实世界的预测通常需要更多的东西，需要进一步了解如何针对各种情况进行预测。

二、定义预测任务

        在设计预测模型之前，需要确定两件事：

        （1）做出预测时可获得哪些信息（特征）。

        （2）以及您需要预测值（目标）的时间段。

        实际上，预测原点是您在预测期间拥有训练数据的最后一次。直到起点的所有东西都可以用来创建特征。

        预测范围是您进行预测的时间。我们经常通过其范围内的时间步数来描述预测：例如，“1-step”预测或“5-step”预测。预测范围描述了目标。

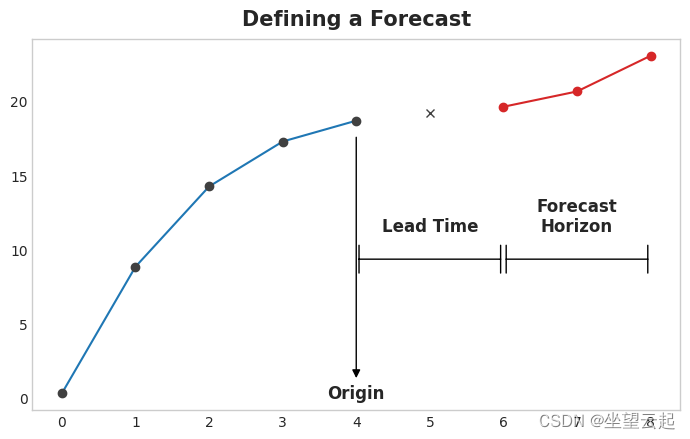
         起点和预测范围之间的时间是预测的提前时间（或有时是延迟）。预测的提前期由从起点到地平线的步数来描述：例如“提前 1 步”或“提前 3 步”预测。 在实践中，由于数据采集或处理的延迟，预测可能需要提前多个步骤开始。

三、为预测准备数据

        为了使用机器学习算法预测时间序列，我们需要将序列转换为可以与这些算法一起使用的数据帧。

        我们创建了一个滞后的特征集。我们如何做到这一点取决于预测任务。

        数据框中的每一行代表一个预测。 该行的时间索引是预测范围内的第一次，但我们将整个范围的值安排在同一行中。 对于多步预测，这意味着我们需要一个模型来产生多个输出，每个输出一个。

import numpy as np
import pandas as pd
 
N = 20
ts = pd.Series(
    np.arange(N),
    index=pd.period_range(start='2010', freq='A', periods=N, name='Year'),
    dtype=pd.Int8Dtype,
)
 
# Lag features
X = pd.DataFrame({
    'y_lag_2': ts.shift(2),
    'y_lag_3': ts.shift(3),
    'y_lag_4': ts.shift(4),
    'y_lag_5': ts.shift(5),
    'y_lag_6': ts.shift(6),    
})
 
# Multistep targets
y = pd.DataFrame({
    'y_step_3': ts.shift(-2),
    'y_step_2': ts.shift(-1),
    'y_step_1': ts,
})
 
data = pd.concat({'Targets': y, 'Features': X}, axis=1)
 
data.head(10).style.set_properties(['Targets'], **{'background-color': 'LavenderBlush'}) \
                   .set_properties(['Features'], **{'background-color': 'Lavender'})

        上面说明了如何准备数据集，类似于定义预测图：使用五个滞后特征的两步提前期的三步预测任务。 原始时间序列是 y_step_1。 我们可以填写或删除缺失值。

四、多步预测策略

        有许多策略可以生成预测所需的多个目标步骤。 我们将概述四种常见的策略，每种策略都有优点和缺点。

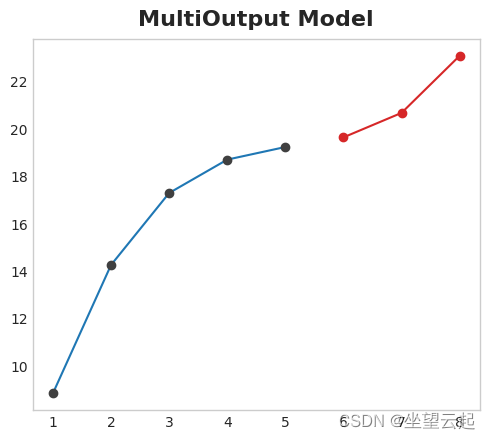
1、Multioutput model

        使用自然产生多个输出的模型。 线性回归和神经网络都可以产生多个输出。 这种策略简单而有效，但不可能适用于您可能想要使用的每种算法。 例如，XGBoost 无法做到这一点。

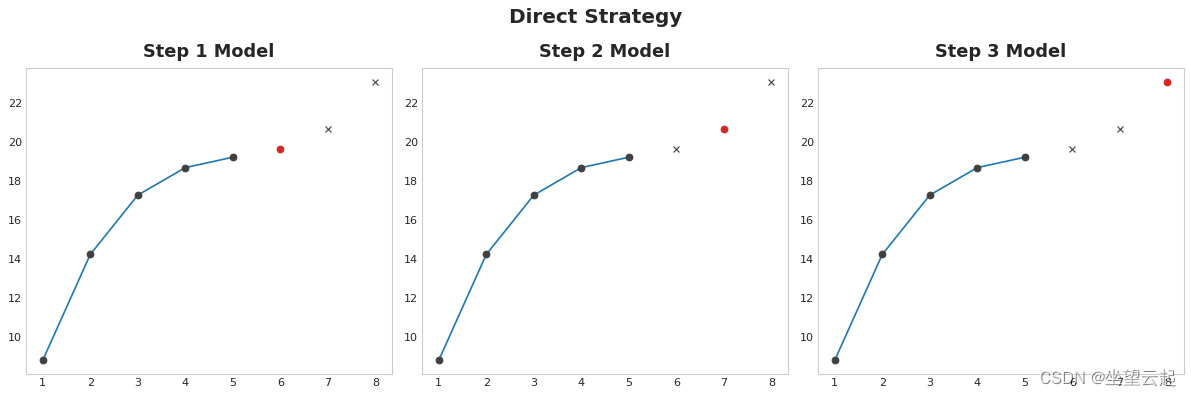
 2、Direct strategy

        为视野中的每一步训练一个单独的模型：一个模型预测提前 1 步，另一个预测提前 2 步，依此类推。 提前 1 步预测与提前 2 步（等等）是不同的问题，因此它可以帮助让不同的模型对每一步进行预测。 缺点是训练大量模型的计算成本可能很高。

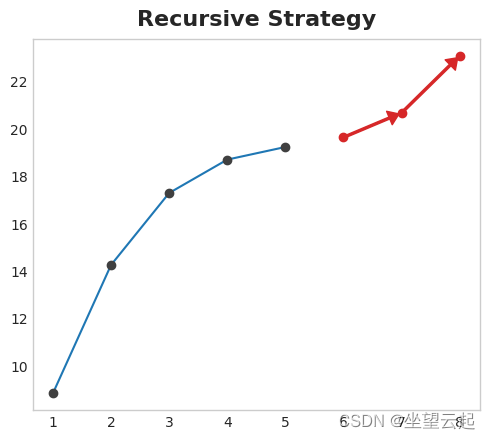
3、Recursive strategy 

        训练一个单步模型并使用其预测来更新下一步的滞后特征。使用递归方法，我们将模型的 1 步预测反馈回同一模型，以用作下一个预测步骤的滞后特征。我们只需要训练一个模型，但由于错误会一步一步地传播，因此长期预测可能不准确。

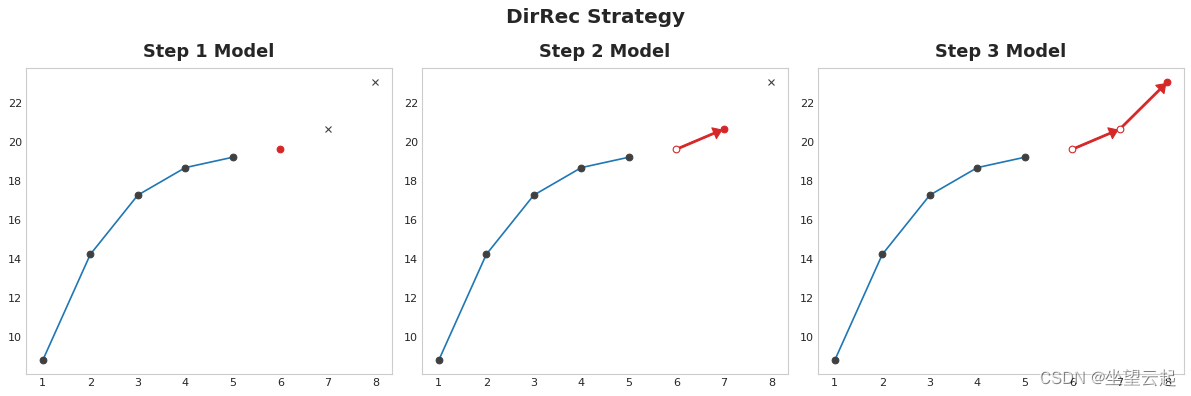
 4、DirRec strategy

        直接策略和递归策略的组合：为每个步骤训练一个模型，并使用来自先前步骤的预测作为新的滞后特征。 逐步地，每个模型都会获得一个额外的滞后输入。 由于每个模型总是有一组最新的滞后特征，DirRec 策略可以比 Direct 更好地捕获串行依赖，但它也可能遭受像 Recursive 这样的错误传播。

五、示例 - 流感趋势 

        在此示例中，我们将对流感趋势数据应用 MultiOutput 和 Direct 策略，这一次对训练期之后的多个星期进行真实预测。

        我们将我们的预测任务定义为 8 周的时间范围和 1 周的提前期。 换句话说，我们将从下周开始预测八周的流感病例。

        隐藏单元设置示例并定义辅助函数 plot_multistep。

from pathlib import Path
from warnings import simplefilter
 
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
from xgboost import XGBRegressor
 
simplefilter("ignore")
 
# Set Matplotlib defaults
plt.style.use("seaborn-whitegrid")
plt.rc("figure", autolayout=True, figsize=(11, 4))
plt.rc(
    "axes",
    labelweight="bold",
    labelsize="large",
    titleweight="bold",
    titlesize=16,
    titlepad=10,
)
plot_params = dict(
    color="0.75",
    style=".-",
    markeredgecolor="0.25",
    markerfacecolor="0.25",
)
%config InlineBackend.figure_format = 'retina'
 
 
def plot_multistep(y, every=1, ax=None, palette_kwargs=None):
    palette_kwargs_ = dict(palette='husl', n_colors=16, desat=None)
    if palette_kwargs is not None:
        palette_kwargs_.update(palette_kwargs)
    palette = sns.color_palette(**palette_kwargs_)
    if ax is None:
        fig, ax = plt.subplots()
    ax.set_prop_cycle(plt.cycler('color', palette))
    for date, preds in y[::every].iterrows():
        preds.index = pd.period_range(start=date, periods=len(preds))
        preds.plot(ax=ax)
    return ax
 
 
data_dir = Path("../input/ts-course-data")
flu_trends = pd.read_csv(data_dir / "flu-trends.csv")
flu_trends.set_index(
    pd.PeriodIndex(flu_trends.Week, freq="W"),
    inplace=True,
)
flu_trends.drop("Week", axis=1, inplace=True)

        首先，我们将准备我们的目标系列以进行多步预测。 一旦完成，训练和预测将非常简单。

def make_lags(ts, lags, lead_time=1):
    return pd.concat(
        {
            f'y_lag_{i}': ts.shift(i)
            for i in range(lead_time, lags + lead_time)
        },
        axis=1)
 
 
# Four weeks of lag features
y = flu_trends.FluVisits.copy()
X = make_lags(y, lags=4).fillna(0.0)
 
 
def make_multistep_target(ts, steps):
    return pd.concat(
        {f'y_step_{i + 1}': ts.shift(-i)
         for i in range(steps)},
        axis=1)
 
 
# Eight-week forecast
y = make_multistep_target(y, steps=8).dropna()
 
# Shifting has created indexes that don't match. Only keep times for
# which we have both targets and features.
y, X = y.align(X, join='inner', axis=0)

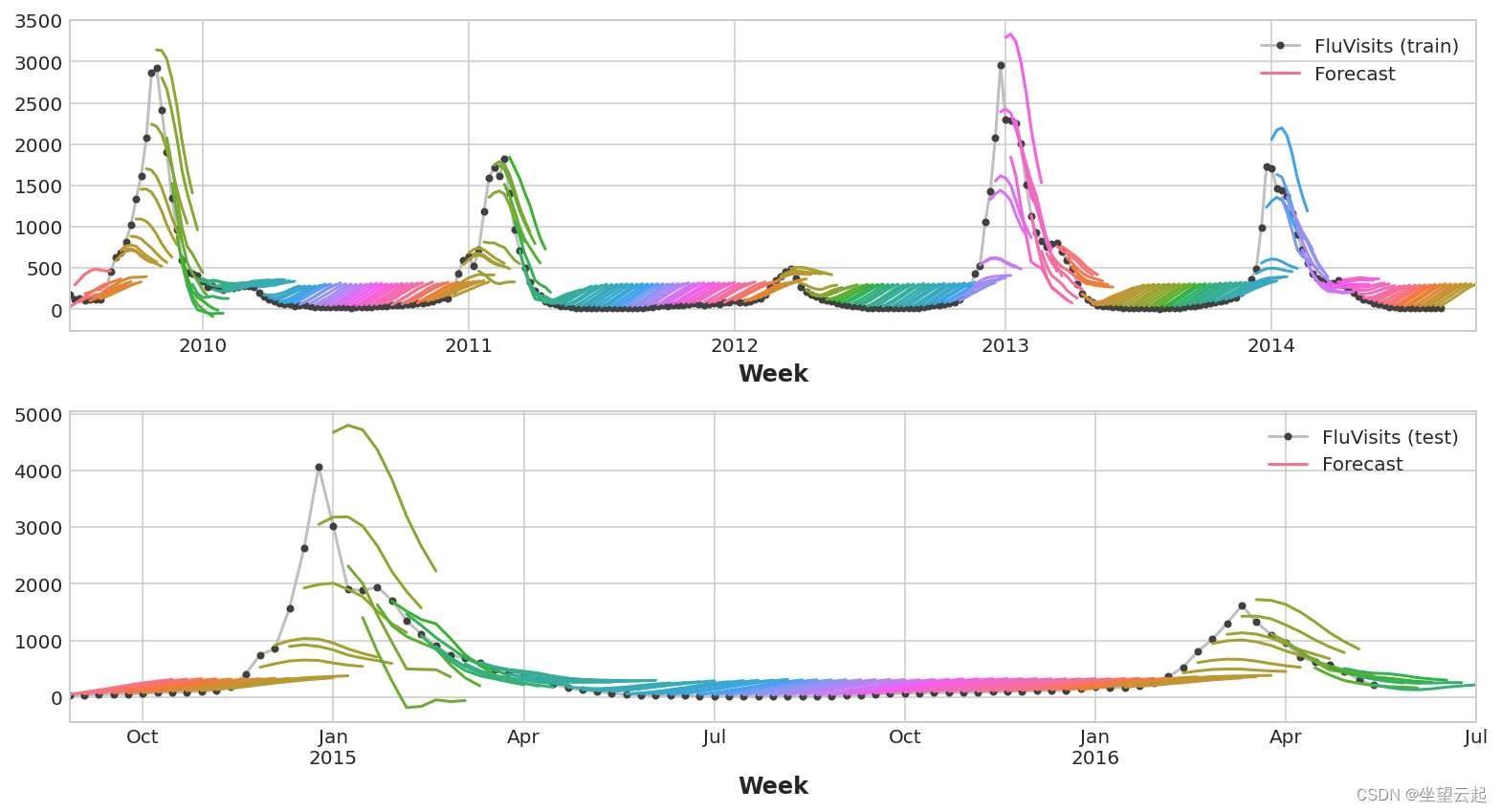
1、多输出模型

        我们将使用线性回归作为多输出策略。 一旦我们为多个输出准备好数据，训练和预测就和往常一样了。

# Create splits
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, shuffle=False)
 
model = LinearRegression()
model.fit(X_train, y_train)
 
y_fit = pd.DataFrame(model.predict(X_train), index=X_train.index, columns=y.columns)
y_pred = pd.DataFrame(model.predict(X_test), index=X_test.index, columns=y.columns)

        请记住，多步模型将为用作输入的每个实例生成完整的预测。 训练集中有 269 周，测试集中有 90 周，我们现在对这些周中的每一周都有一个 8 步预测。

train_rmse = mean_squared_error(y_train, y_fit, squared=False)
test_rmse = mean_squared_error(y_test, y_pred, squared=False)
print((f"Train RMSE: {train_rmse:.2f}\n" f"Test RMSE: {test_rmse:.2f}"))
 
palette = dict(palette='husl', n_colors=64)
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(11, 6))
ax1 = flu_trends.FluVisits[y_fit.index].plot(**plot_params, ax=ax1)
ax1 = plot_multistep(y_fit, ax=ax1, palette_kwargs=palette)
_ = ax1.legend(['FluVisits (train)', 'Forecast'])
ax2 = flu_trends.FluVisits[y_pred.index].plot(**plot_params, ax=ax2)
ax2 = plot_multistep(y_pred, ax=ax2, palette_kwargs=palette)
_ = ax2.legend(['FluVisits (test)', 'Forecast'])

Train RMSE: 389.12
Test RMSE: 582.33

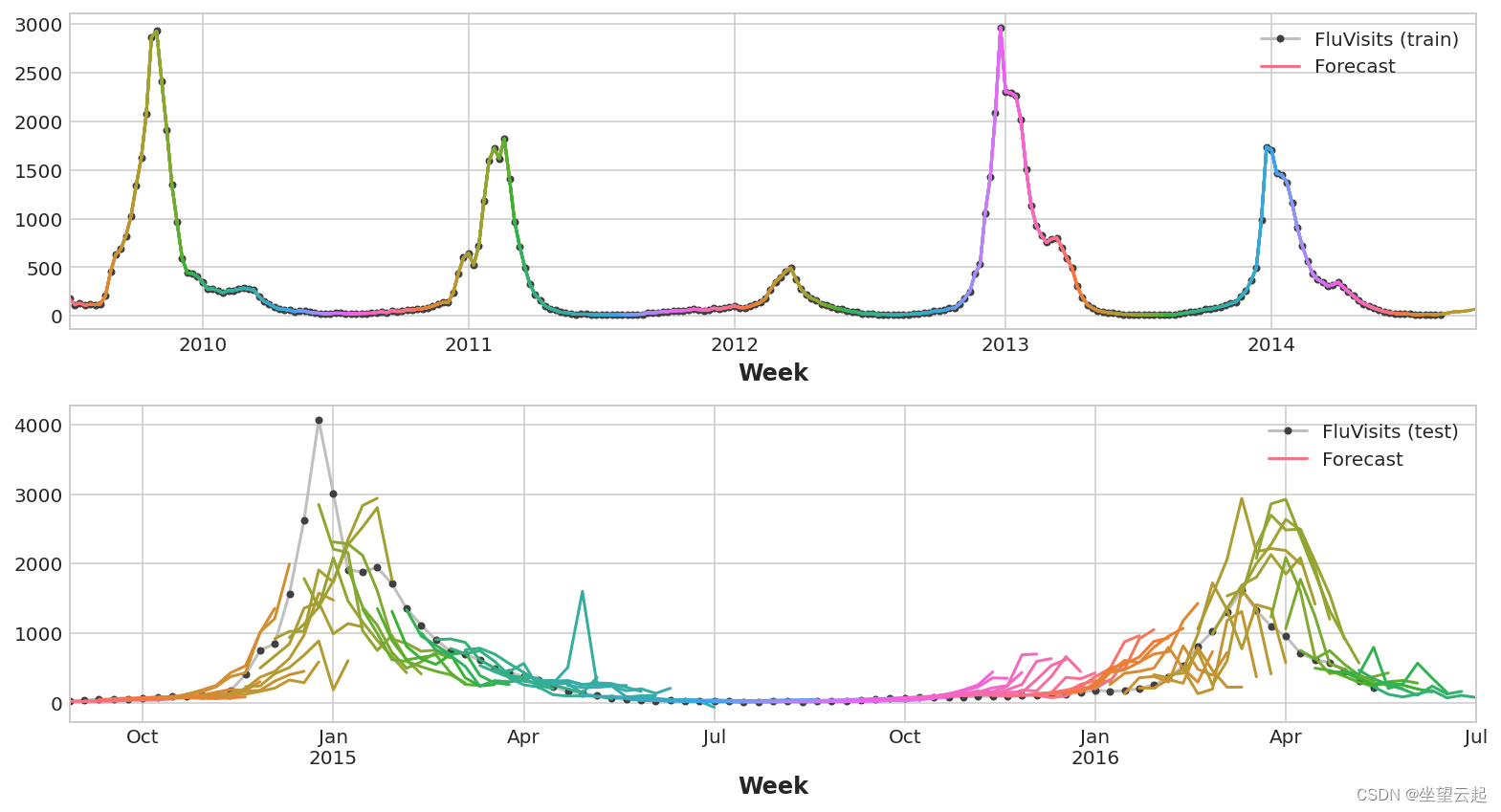
2、直接策略

        XGBoost 不能为回归任务生成多个输出。 但是通过应用直接减少策略，我们仍然可以使用它来生成多步预测。 这就像用 scikit-learn 的 MultiOutputRegressor 包装它一样简单。

from sklearn.multioutput import MultiOutputRegressor
 
model = MultiOutputRegressor(XGBRegressor())
model.fit(X_train, y_train)
 
y_fit = pd.DataFrame(model.predict(X_train), index=X_train.index, columns=y.columns)
y_pred = pd.DataFrame(model.predict(X_test), index=X_test.index, columns=y.columns)

        这里的 XGBoost 显然在训练集上过度拟合。 但在测试集上，它似乎能够比线性回归模型更好地捕捉到流感季节的一些动态。 通过一些超参数调整它可能会做得更好。

train_rmse = mean_squared_error(y_train, y_fit, squared=False)
test_rmse = mean_squared_error(y_test, y_pred, squared=False)
print((f"Train RMSE: {train_rmse:.2f}\n" f"Test RMSE: {test_rmse:.2f}"))
 
palette = dict(palette='husl', n_colors=64)
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(11, 6))
ax1 = flu_trends.FluVisits[y_fit.index].plot(**plot_params, ax=ax1)
ax1 = plot_multistep(y_fit, ax=ax1, palette_kwargs=palette)
_ = ax1.legend(['FluVisits (train)', 'Forecast'])
ax2 = flu_trends.FluVisits[y_pred.index].plot(**plot_params, ax=ax2)
ax2 = plot_multistep(y_pred, ax=ax2, palette_kwargs=palette)
_ = ax2.legend(['FluVisits (test)', 'Forecast'])

Train RMSE: 1.22
Test RMSE: 526.45

         要使用 DirRec 策略，您只需将 MultiOutputRegressor 替换为另一个 scikit-learn 包装器 RegressorChain。 我们需要自己编写代码的递归策略。