人工智能数学基础--概率与统计7：学习中一些术语的称呼或表示变化说明以及独立事件的一些补充推论

一、概念表示变化说明

笔者最开始学习概率论时，是以美版M.R.斯皮格尔等著作的《概率与统计》作为教材学习，学习过程中发现部分内容理解困难，之所以这样，一是这本书的内容太古老，教材是2002年翻译出版的，二是部分内容翻译不是很好，后来感谢AI大佬herosunly提供了陈希孺老师编写的《概率论与数理统计》，2009年出版的，学习起来感觉轻松多了，但这两本教材在个别术语表示上有所区别，在此记录一下：

1. 事件A和B的并集，美版表示为：A∪B，陈版称为A和B的和，表示为A+B；

2. 事件A和B的交集，美版表示为：A∩B，陈版称为A和B的积、乘积或交，表示为AB；

3. 事件集合A的补集，也称为A的对立事件，美版表示为：A’，陈版表示为A^c或

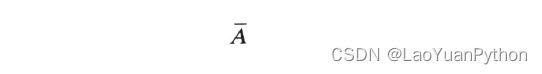
4. 多个事件A_i的并（和）美版记为：
   
   陈版记为：
   

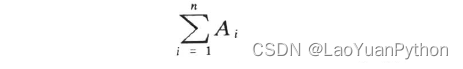
5. 多个事件A_i的交（积）陈版记为：
   

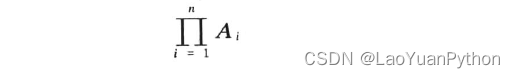
二、独立事件的几个补充推论

这几个推论在前面博文中没有介绍，在此单独介绍一下。

1. 独立事件的任一部分也独立，例如A、B、C、D四事件独立，则A、C也独立；
2. 由独立事件决定的事件也独立，所谓决定就是通过运算等进行组合成新事件，这个推论要求不同新事件的基础事件必须不同，当然某些情况下有相同基础事件的新事件也可能是独立的，例如A、B、C、D四事件独立，E=A-B，F = C+D，则E和F是独立的；
3. 如果一系列时间A1、A2，…相互独立，则其中任意部分事件改为其对立事件，所得事件认为相互独立。例如A1’、A2相互独立；

更多人工智能数学基础请参考专栏《人工智能数学基础》。

写博不易，敬请支持：

如果阅读本文于您有所获，敬请点赞、评论、收藏，谢谢大家的支持！

关于老猿的付费专栏

1. 付费专栏《https://blog.csdn.net/laoyuanpython/category_9607725.html 使用PyQt开发图形界面Python应用》专门介绍基于Python的PyQt图形界面开发基础教程，对应文章目录为《 https://blog.csdn.net/LaoYuanPython/article/details/107580932 使用PyQt开发图形界面Python应用专栏目录》；
2. 付费专栏《https://blog.csdn.net/laoyuanpython/category_10232926.html moviepy音视频开发专栏 )详细介绍moviepy音视频剪辑合成处理的类相关方法及使用相关方法进行相关剪辑合成场景的处理，对应文章目录为《https://blog.csdn.net/LaoYuanPython/article/details/107574583 moviepy音视频开发专栏文章目录》；
3. 付费专栏《https://blog.csdn.net/laoyuanpython/category_10581071.html OpenCV-Python初学者疑难问题集》为《https://blog.csdn.net/laoyuanpython/category_9979286.html OpenCV-Python图形图像处理 》的伴生专栏，是笔者对OpenCV-Python图形图像处理学习中遇到的一些问题个人感悟的整合，相关资料基本上都是老猿反复研究的成果，有助于OpenCV-Python初学者比较深入地理解OpenCV，对应文章目录为《https://blog.csdn.net/LaoYuanPython/article/details/109713407 OpenCV-Python初学者疑难问题集专栏目录 》
4. 付费专栏《https://blog.csdn.net/laoyuanpython/category_10762553.html Python爬虫入门 》站在一个互联网前端开发小白的角度介绍爬虫开发应知应会内容，包括爬虫入门的基础知识，以及爬取CSDN文章信息、博主信息、给文章点赞、评论等实战内容。

前两个专栏都适合有一定Python基础但无相关知识的小白读者学习，第三个专栏请大家结合《https://blog.csdn.net/laoyuanpython/category_9979286.html OpenCV-Python图形图像处理 》的学习使用。

对于缺乏Python基础的同仁，可以通过老猿的免费专栏《https://blog.csdn.net/laoyuanpython/category_9831699.html 专栏：Python基础教程目录）从零开始学习Python。

如果有兴趣也愿意支持老猿的读者，欢迎购买付费专栏。

老猿Python，跟老猿学Python！

☞ ░ 前往老猿Python博文目录 https://blog.csdn.net/LaoYuanPython ░