基于Cat混沌与高斯变异的改进灰狼优化算法

摘要：针对基本灰狼优化算法在求解复杂问题时同样存在依赖初始种群、过早收敛、易陷入局部最优等缺点，提出一种改进的灰狼优化算法应用于求解函数优化问题中。该算法首先利用混沌Cat映射产生灰狼种群的初始位置，为算法全局搜索过程的种群多样性奠定基础；同时引入粒子群算法中的个体记忆功能以便增强算法的局部搜索能力和加快其收敛速度；最后采用高斯变异扰动和优胜劣汰选择规则对当前最优解进行变异操作以避免算法陷入局部最优。

1.灰狼优化算法

基础灰狼算法的具体原理参考，我的博客：https://blog.csdn.net/u011835903/article/details/107716390

2. 改进灰狼优化算法

2.1 混沌反向学习策略的种群初始化

为保持种群多样性，使初始种群个体尽可能均匀分布，本文结合混沌初始化方法和基于反向学习初始化策略，提出了混沌反向学习初始化策略，有助于加快算法的收敛速度。将混沌映射序列与传统优化算法相结合的混合优化算法纷纷产生，而且取得了比较良好的结果，但是，这些算法均基于Logistic映射，寻优速度受到Logistic遍历不均匀性的影响，同时Logistic映射对初值设置敏感，且遍历性和均匀性都相对较差（映射点边缘处密度很高而区间中央密度较低），这将直接影响混沌搜索的遍历性能。

本文研究了Cat映射的结构和混沌特性，Cat映射是一个二维的可逆混沌映射，其动力学方程如下：
[ x n + 1 y n + 1 ] = [ 1 1 1 2 ] [ x n y n ]   m o d   1 (8) \left[

\right]=\left[\right]\left[\right] \bmod 1 \tag{8} [xn+1​yn+1​​]=[11​12​][xn​yn​​]mod1(8)
该映射结构简单，具有更好的遍历均匀性和更快的迭代速度，且在[0，1]间产生的混沌序列分布均匀。基于混沌反向学习策略初始化种群的具体步骤为：首先利用Cat混沌序列产生 N 个初始解 X i ，然后为每个初始解均按照以下方式产生相对应的反向解：
$$O{P}_i=K\left(X_{\min }^d+X_{\max }^d\right)-X_i\text{\hspace{1em}(9)}$$
其中， $K$为[0，1]间的随机数； $O{P}_i$ 为每个初始解 $X_i$ 所对应的反向解； $X_{min}^d、X_{max}^d$ 分别表示所有初始解中第 d维向量的最小值和最大值。最后，对初始解和反向解进行合并按照适应度值进行升序（求最小值）排序，选取适应度值前 N 个较优的解作为初始种群。

2. 2 引入个体记忆策略

在基本GWO算法中，虽然考虑了个体当前位置与群体历史最优位置，实现了灰狼种群信息的交流，最终通过个体在搜索空间移动收敛得到最优解，但是基本GWO算法未考虑灰狼个体自身的经验，因此在式（6）的基础上考虑PSO算法中的个体记忆功能，其具体表达式为 ：
X i d ( t + 1 ) = b 1 ⋅ ∑ j = α , β , δ w j X i , j d ( t + 1 ) + b 2 ⋅ rand ⁡ 3 ( P best  d − X i d ( t ) ) (10)

\tag{10} Xid​(t+1)=b1​⋅∑j=α,β,δ​wj​Xi,jd​(t+1)+b2​⋅rand3​(Pbest d​−Xid​(t))​(10)
其中 $ran{d}_3$ 表示 [0,1] 间的随机变量； $b_1、b_2$ 分别表示群体交流系数与个体记忆系数，它们是 [0,1] 之间的常数；$P_{best}^d$ 表示第 i 只灰狼经历过的最佳位置。通过调节 $b_1、b_2$ 的值，可以平衡群体交流与个体记忆对搜索的影响。

2.3改进非线性收敛因子策略

本文提出的改进非线性公式如下：
$$a=2{\left(1-t/t_{\max }\right)}^k\text{\hspace{1em}(11)}$$
其中， $t$ 为当前迭代次数， $tmax$ 为最大迭代次数， $k$ 为非线性调节参数。由公式（11）知，收敛因子$a$ 随进化迭代次数增加而非线性动态变化，能够为有效地平衡灰狼优化算法的全局搜索和局部搜索能力提供有利前提。

2.4 高斯变异和优胜劣汰选择策略

变异算子可以避免算法陷入局部最优，同时也能保持种群个体的多样性。为了降低基本GWO算法出现早熟和陷入局部最优的概率，本文以一定概率 $p$ 对当前最优解 $X_{\alpha }(t)$ 进行高斯变异操作并借鉴“贪婪”选择思想，实行优胜劣汰的选择规则。高斯变异算子具体表达式如下：
$$X_{\text{best }}(t+1)=X_{\alpha }(t)(1+\mathrm{Gaussion}(\sigma ))\text{\hspace{1em}(12)}$$
其中， $X_{best} (t+1) $表示变异后个体的位置， Gaussion(σ)为满足高斯分布的随机变量。全局最优位置更新如下：
X α ( t + 1 ) = { X best  ( t + 1 ) ,  其他  X α ( t ) , f ( X best  ( t + 1 ) ) > f ( X α ( t ) )  且  rand ⁡ 4 < p (13) X_{\alpha}(t+1)=\left\{

\right. \tag{13} Xα​(t+1)={Xbest ​(t+1), 其他 Xα​(t),f(Xbest ​(t+1))>f(Xα​(t)) 且 rand4​<p​(13)
其中， rand 4 表示[0，1]间的随机变量， p 为优胜劣汰选择概率， f(⋅) 为个体的适应度值。从公式（13）可知，通过对当前全局最优解 X α (t) 进行变异操作，可以避免陷入局部最优（若当前全局最优是局部最优值）。采用该选择策略，可使种群朝着最优解的方向进化，同时有效地提高算法的搜索效率。

本文提出的改进的灰狼优化算法（记为IGWO）步骤如下：
步骤1 设置算法参数，种群规模 N、 最大迭代次数t max 、 非线性调节参数 k、 群体交流系数 b 1 、 个体记忆系数 b 2 、 高斯变异优胜劣汰选择概率 p 、初始化 rand 1 、rand 2 、rand 3 、rand 4 、a、A di 、Cdi等，其中 i=1,2,⋯,N ，d=1,2,⋯,D 。
步骤2 设定所需优化参数的允许范围，在搜索空间中利用 3.1 节所描述的 Cat 混沌映射初始化狼群 X i ，i=1,2,⋯,N ，狼群规模为 N 。
步骤3 计算群体中每个个体的适应度值并排序，进而确定历史最优解 X α ，次最优解 X β ，第三最优解 X δ 。
步骤4 对每只灰狼个体，按公式（6）初步计算灰狼位置。
步骤5 考虑PSO算法中个体记忆功能，按公式（10）进一步更新的灰狼位置。
步骤6 对当前群体中最优灰狼个体执行2.4节所描述的高斯变异操作，并按优胜劣汰选择概率 p ，确定是否接受变异后的新的灰狼个体位置。
步骤7 迭代次数 t=t+1 ，根据公式（11）计算出改进后收敛因子 a 的值，进而更新 rand 1 、rand 2 、rand 3 、rand 4 、A di 、Cdi 等变量， i=1,2,⋯,N ， d=1,2,⋯,D 。步骤8 判断算法的当前迭代次数是否达到最大迭代次数，若满足，则进入步骤9，否则返回执行步骤3。
步骤9 返回最优灰狼个体位置 X α ，则算法结束。

3.实验结果

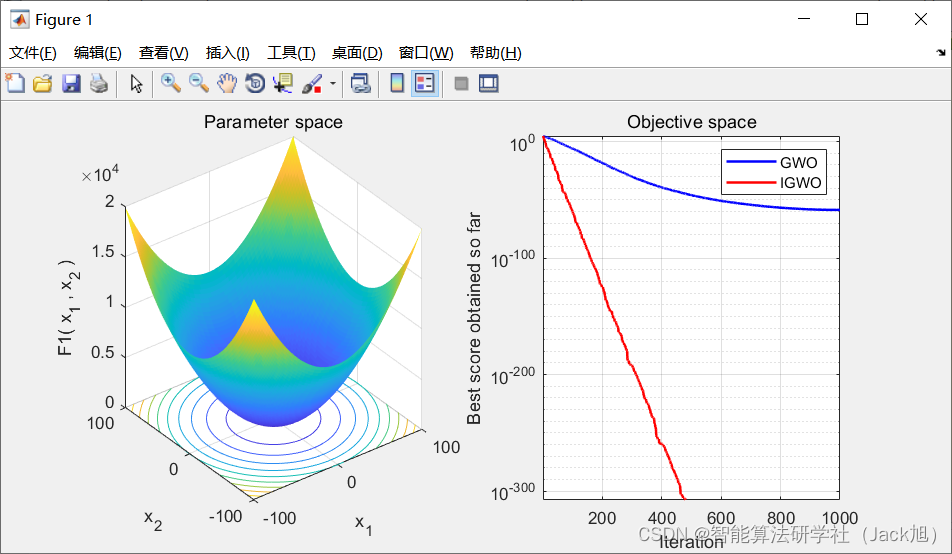
4.参考文献

[1]徐辰华,李成县,喻昕,黄清宝.基于Cat混沌与高斯变异的改进灰狼优化算法[J].计算机工程与应用,2017,53(04):1-9+50.

5.Matlab代码

6.Python代码