动态时间规整算法——DTW

   没有做过机器学习的小伙伴们对这个算法应该不是特别的了解，因为机器学习经常会用到这个算法。再将这个算法之前，我们先看一下初中的知识点。

欧几里得距离

    在讲解动态时间规整算法（Dynamic Time Warping， DTW）之前，我们先来了解一下，在日常生活中，用来计算两点的距离，我们是怎么进行的。回想一下初中的数学知识点——几何距离，如下图所示的二维空间中计算A点到B点的距离。

其中A点和B点的坐标分别为：A(1,2) 和 B(2,1)，如果要算A点到B点的距离，那么计算方式为：

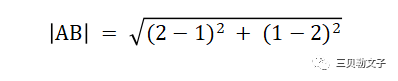
    如果是在三维的空间，如下图所示：

其中A点和B点的坐标分别为：A(0,1,2) 和 B(1,3,1)，如果要算A点到B点的距离，那么计算方式为：

    以此类推，对于n维的空间，距离公式应该表达为：

    从初中用到现在，那么你知道这个和计算距离的方法是谁发明的吗？（应该不是我嘿嘿嘿~~）。发明这个方法的大神就是欧几里得，计算的距离公式也叫做欧几里得距离，简称欧氏距离。

   

    你会好奇，无端端讲了欧几里得距离做什么，我们先不急，继续往下看。

动态时间规整

    上面我们讲到了欧几里得距离，举的两个例子也是针对空间上的位置计算，那么如果现在是两个时序信号呢，也就是加上了时间维度，这种计算是否还能够成立，接下来我们来看一下一个小例子，如下图所示，假设用户A和用户B两个人在读 “我爱中国”。用户A说的比较干脆，用户B说的有点拖音（即用户A说：“我爱中国”，用户B说“我~爱中国”，差别就是用户B在说我的时候拖了一下音）。我们假设用户A的发音是【1,2,1,3】，用户B的发音是【1,1,2,1,3】，两个用户的发音区别就是用户B在说第一个字的时候拖了音，如下图所示：

    因为用户A和用户B讲的是同一句话，并且意思也是一样的，那么按照机器学习理论来说，它们的相似性应该很相似，也就是距离很近，OK，那如果我们认为是n维数据，然后使用n维的欧氏距离来计算一下这两者的距离，表达式为：

    通过上面表达式计算得知，用户A和用户B的距离为：

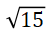
这也太远了吧。不是说相似吗。

    细心的你已经发现了一个问题，欧几里得距离的计算方式是运用在空间上的比较多。对于时间序列，欧几里得距离计算方法好像显得不那么友好了。所以为了解决这个问题，日本的一位学者 Itakura 在60年代提出了动态时间规整算法（Dynamic Time Warping，DTW），用于衡量两个长度不同的时间序列的相似度。把未知量伸长或缩短(压扩)，直到与参考模板的长度一致，在这一过程中，未知序列会产生扭曲或弯折，以便其特征量与标准模式对应。具体做法如下图所示：

    图中的红线就是将用户B的语音序列和用户A的语音序列对应起来，实现时间规整的思想，这样计算的距离才会是最短的。

    那么DTW算法的步骤如下：

1. 计算两个序列各个点之间的距离矩阵；

2. 寻找一条从矩阵左上角到右下角的路径，使得路径上的元素和最小：

   我们称路径上的元素之和为路径的长度，那么怎么去寻找长度最小的路径呢？

   矩阵从左上角到右下角的路径长度有以下性质：

   (1) 当前的路径长度 = 前一步的路径长度 + 当前元素的大小

   (2) 路径上的某个元素（i，j），它的前一个元素只可能为以下三者之一：

         a.  左边的相邻元素（i, j-1）

         b. 上面的相邻元素（i-1, j）

         c.  左上方的相邻元素（i-1, j-1）

   表达式表示为：

   

        3. 寻找到最后的右下角就是路径的最小路径。

接下来，我们来对用户A和用户B进行动态时间规整步骤的解析：

首先，将序列A和序列B的矩阵列举出来，然后元素两两相减：

    通过相减后得到上面的一个矩阵，接下来就定义一个结果矩阵来存放路径的长度，如下图所示，初始化结果矩阵，然后计算最上面一行和最左边一列的路径和，因为根据上面公式得到，第一行的每一个节点i只能从它的左边i-1过来，而每一列的每一个节点j只能从它的上一个节点j-1过来。然后再计算其他的路径，根据公式，在其他的节点中（i，j）的路径前一个点有三个（i，j-1）、（i-1，j-1）、（i-1，j），分别计算取最小值作为当前的数值。依次计算遍历。

最后得到的结果矩阵为：

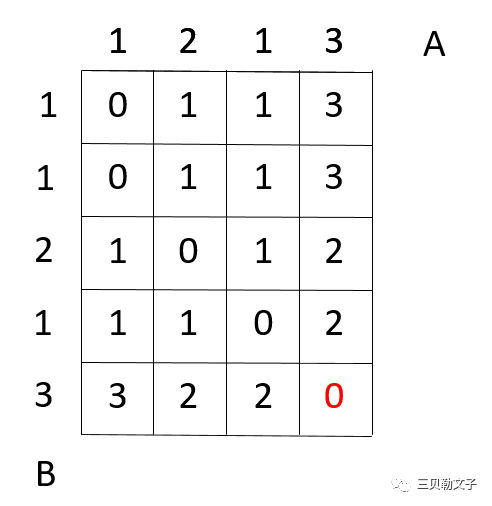
    最右下角的元素数值就是用户A和用户B两个序列的距离，结果为0，说明用户A和用户B所说的话是一样的。

DTW的代码如下：

#include<iostream>
#include<string.h>
#include<stdlib.h>
using namespace std;
#define NUM1 6       //序列中样本点的个数简单起见，假设2个序列的样本点一样多
#define NUM2 5
#define max 999
#define Min(a,b) (a<b?a:b)
 
int main()
{
  int i,j,k;
  //int a[NUM1],b[NUM2];
 
  int b[4]={1,2,1,3};
  int a[6]={1,1,2,1,3};
 
  int distance[NUM1+1][NUM2+1];
  int output[NUM1+1][NUM2+1];
 
  memset(distance,0,sizeof(distance));
  memset(output,0,sizeof(output));
  for(i=0;i<=NUM1;i++)
  {
    for(j=0;j<=NUM2;j++)
    {
      distance[i][j]=max;
      output[i][j]=max;
    }
  }
  distance[0][0]=0;
  output[0][0]=0;
 
  //for(i=0;i<NUM1;i++)  cin>>a[i];
  //for(i=0;i<NUM2;i++)  cin>>b[i];
 
  for(i=1;i<=NUM1;i++)
    for(j=1;j<=NUM2;j++)
      distance[i][j]=abs(b[j-1]-a[i-1]);    //计算点与点之间的欧式距离
 
  for(i=1;i<NUM1;i++)
  {
    for(j=1;j<NUM2;j++)
      cout<<distance[i][j]<<'\t';
    cout<<endl;
  } //输出整个欧式距离的矩阵
  cout<<endl;
 
 
  for(i=1;i<NUM1;i++)
    for(j=1;j<NUM2;j++)  
      output[i][j]=Min ( Min(output[i-1][j-1],output[i][j-1]) ,output[i-1][j] )+distance[i][j];
  //DP过程，计算DTW距离
 
  for(i=1;i<NUM1;i++)
  {
    for(j=1;j<NUM2;j++)
      cout<<output[i][j]<<'\t';
    cout<<endl;
  } //输出最后的DTW距离矩阵，其中output[NUM][NUM]为最终的DTW距离和
  
  system("pause");
  return 0;
}

结果输出为：