-
计数排序和排序的稳定性
前面我们说的都是通过比较来进行排序,这次我说一下非比较排序。然后,把排序做一下总结。

1. 计数排序
1.1 基本思想
思想:计数排序又称为鸽巢原理,是对哈希直接定址法的变形应用。 操作步骤:
1. 统计相同元素出现次数
2. 根据统计的结果将序列回收到原来的序列中
我们举个例子:
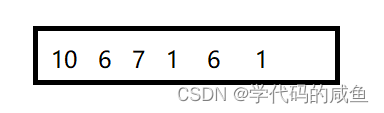
在这组数据中,我们可以看到最大的数是10,所以我们定义一个下标到10的数组,并将数组里的内容全部赋值为0。
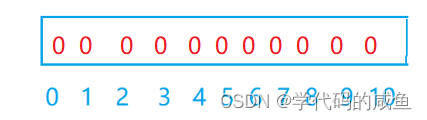
然后,我们遍历原数组,一个值出现几次,它映射的位置就++几次。
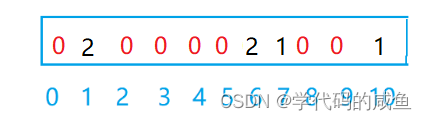
这就是映射后的情况,然后我们再从小到大赋给原数组。
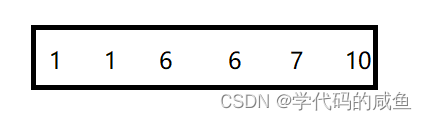
这种映射也叫做绝对映射,但如果数据特别的大,那么绝对映射就会浪费空间了。比如下面的这组数据:
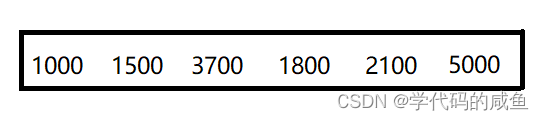
如果这组数据使用绝对映射的话前1000个数就会发生空间浪费。这里,我们就需要使用相对映射。怎样使用相对映射呢?
我们需要找出最小的和最大的两个数据,然后相减就是这个映射数组的大小。
从上组数据中,最大的是5000,最小的是1000,相减就是4000,所以我们需要定义4001个空间。
此时,0代表的就是1000,4000代表的就是5000。此时,根据相对位置进行映射。1500就是500,3700就是2700,1800就是800,2100就是1100。1.2 具体实现
基本思路说完了,我们就需要将它实现一下:
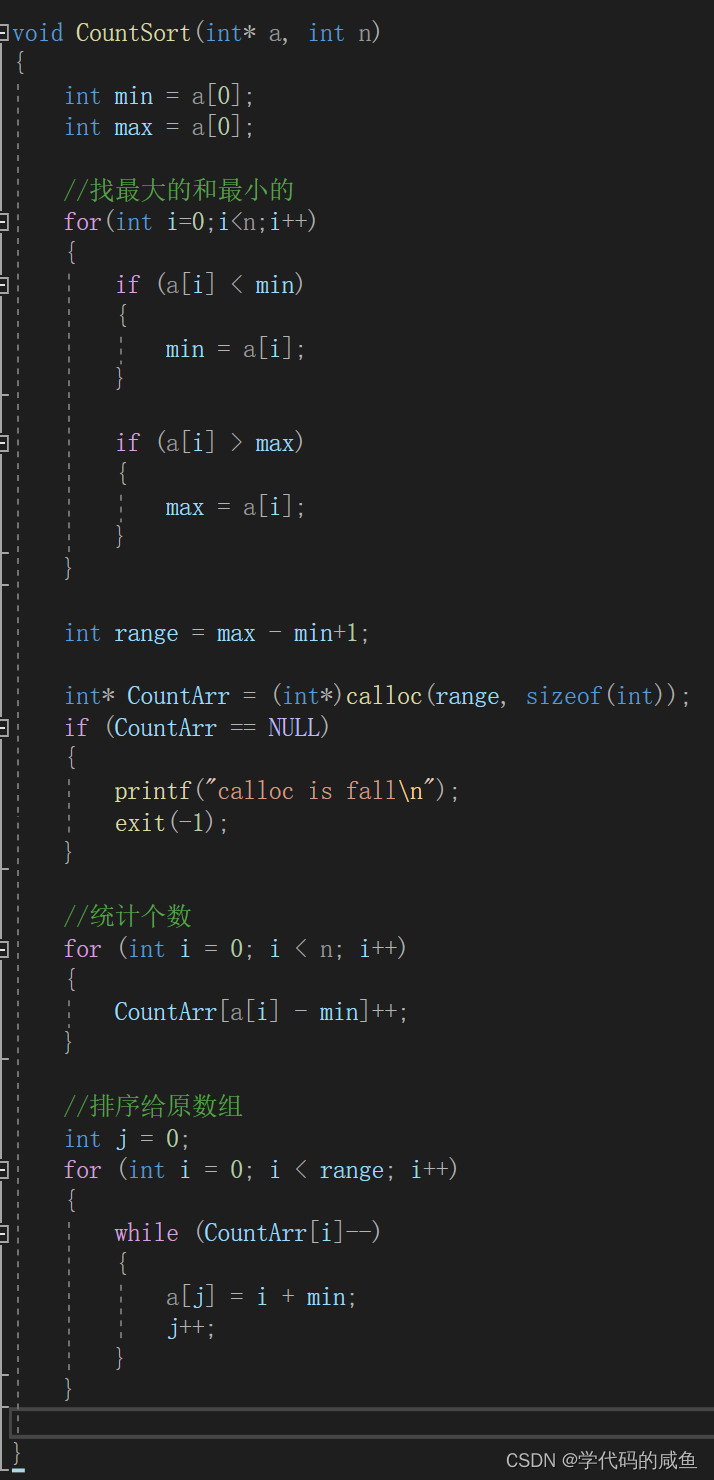
这里需要重点理解的就是统计个数和排序那两块,实现是不难的。
此时,我们需要再想一个问题:负数行不行呢?

绝对映射,我们不用想,肯定是不行的,那么相对映射行不行呢?
在这里,最大的是2100,最小的是-5000,那我们就需要定义2100-(-5000)=7100。
在这里,1000代表的是6000,-1500代表的是3500,-3700代表的是1300,1800代表的是6800。
计数时6000,3500,1300,6800位置处要++,排序返回原数组时,在这些位置加上-5000,就是原数据,所以负数是可以的。我们来验证一下:
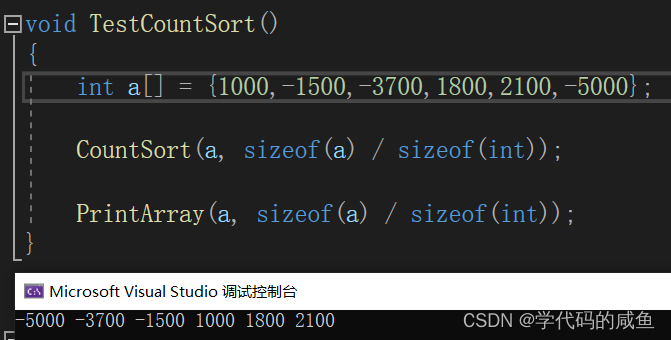
计数排序,我们可以看到适用于范围集中的数据,数组中有负数也是可以的。但是其他类型就不行了,比如浮点、字符串等等。1.3 复杂度
首先,空间复杂度没什么好说的,就是额外开辟的空间:O(range)
时间复杂度,我们来说一下:
前面的两个循环都是n,这没有什么说的,主要最后一个循环可能大家会有问题:

这里面的while循环,当所有的数都减完时,就是原数组里的n,外面的for循环执行的次数是range次。这两个循环没有任何关系,所以,两个循环的复杂度一共执行的次数是n+range,在大O的渐进表示法中时间复杂度为O(n+range)2. 稳定性
2.1 什么是稳定性
可能大家会认为稳定性指的是性能的波动,但是不是这样的。
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
举个例子:
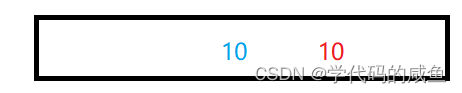
比如一个数组中,有两个相同的数。蓝色的10在红色的10前面。
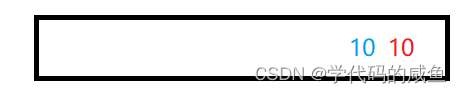
在排完序后,蓝色的10还在红色的10前面,就说明它是稳定的,否则就是不稳定的。2.2 哪些排序是稳定的
哪些排序是稳定的,我们就来分析一下:

直接插入排序,我们根据思想:我们将小的往前插入,大的和相等的不动。所以,我们可以认为它是稳定的。希尔排序,它是不稳定的,因为相同的数据可能被分到不同gap组。
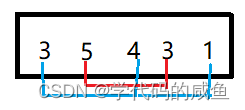
就比如说这组数据,蓝色的3会被调到下标为2的位置,红色的3会被调到下标为1的位置。两者的相对位置不一样了,就是不稳定的。选择排序,它是不稳定的。我们来看这样的一组数据:

我们选出最小的1,和最左边的3进行交换。
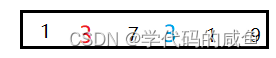
你会发现两个3的相对位置发生了改变。所以它是不稳定的。堆排序,它是不稳定的。我们看下面的数据就知道了:
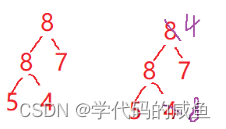
两个8的相对位置发生了变化。冒泡排序,它是稳定的。因为冒泡是两两比较,大的就往后移,小的和相等的就不动。
快速排序,它是不稳定的。因为,每次选key时它是不确定的,它可能将前面的数选到中间。
归并排序,它是稳定的。我们举个例子:
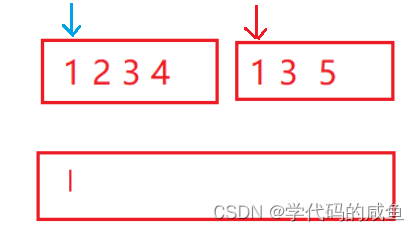
从上面的例子中,如果我们先走的是蓝色,它就是稳定的。下面我再附一张排序的复杂度图:
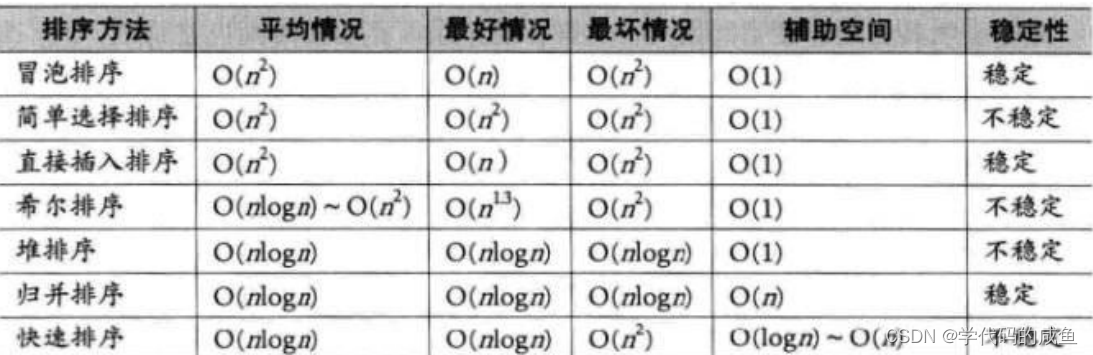
-
相关阅读:
WorkPlus:企业数字化底座,统一数字化办公入口
山东省专精特新|山东省“专精特新”条件|专业申报认定补贴
Share| Membership in the American Society of Professionals in P
PowerBI中导出数据方法汇总
Qt使用Json
使用Postman调试API遇到“400 Bad Request”问题
测试/开发程序员,如何跳出技术瓶颈?一年两年......
UE4 小知识【不断更新中】
【23真题】这套适合考211的同学练手!考察复杂梅森!
【EI会议】2022年人工智能与统计学前沿国际会议(CFAIS 2022)
- 原文地址:https://blog.csdn.net/qq_52154068/article/details/124718376