以动态规划的方式求解最长回文子串

Dynamic Programming (DP) is an algorithmic technique for simplifying a complicated problem by breaking it down into simpler sub-problems in a recursive manner and utilizing the fact that the optimal solution to the overall problem depends upon the optimal solution to its subproblems.

以递归的方式将复杂问题分解为“更简单的子问题”：整体问题的最优解取决于其子问题的最优解

---

leetcode - 5. 最长回文子串
官方动态规划的题解写很抽象，没一个图片，看的差点怀疑智商，后看到如下视频，清楚多了，遂记录下来
使用【动态规划】求解最长回文子串

判断方式：首尾字符比较，之后去掉首尾字符，再比较现有首尾字符。单个字符一定是一个字串

暴力解法状态无法保留，比如[a,b,c,a]中，首尾字符相等，再比较[b,c]，但[b,c]可能之间已经比较过了，现在又需要重新比较下

使用动态规划如下图，注意，这里的二维数组要理解为区间，如 [3,5] 为区间 [b,a,b]

var longestPalindrome = function (s) {
  let n = s.length
  let dp = new Array(n).fill(0).map(() => new Array(n).fill(true))
  for (let i = n - 2; i >= 0; i--) {	// 第一个[b]一定为true，所以从[a,b]开始
    for (let j = i + 1; j < n; j++) {		// 这里的二维数组理解为区间，如[3,5]为区间[b,a,b]
      dp[i][j] = (s[i] == s[j]) && dp[i + 1][j - 1]	// 起点和端点相同，并且内部字串起点和端点也相同，代表是回文子串		[i+1,j-1]代表内部
    }
  }
  let maxstr = ""
  for (let i = 0; i < n; i++) {
    var maxIndex = dp[i].lastIndexOf(true)
    if (maxIndex - i + 1 > maxstr.length) {
      maxstr = s.slice(i, maxIndex + 1)
    }
  }
  return maxstr
};

console.log(longestPalindrome("cabbab"))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

当然，这里的动态规划时间空间复杂度都是 $n^2$，并不是最优解，下面的文章中心扩散解释的还是不错的
中心扩散，暴力，动态规划，马拉车4种方式解决

最长公共子序列

1143. 最长公共子序列

【算法演示】动态规划求解最长公共子序列

状态转移方程如下
d p [ i ] [ j ] = { d p [ i − 1 ] [ j − 1 ] + 1 , a [ i ] = b [ j ] M a x ( d p [ i ] [ j − 1 ] , d p [ i − 1 ] [ j ] ) , a [ i ] ≠ b [ j ] dp[i][j]= \left\{

\right. dp[i][j]={dp[i−1][j−1]+1,a[i]=b[j]Max(dp[i][j−1],dp[i−1][j]),a[i]​=b[j]​

$a[i]=b[j]$ 相等，添加字串长度，否则，取之前计算过的最大字串，如 [a,b,c,d]，[b,a]，尾字符不相等，则取[a,b,c,d]，[b] 和 [a,b,c]，[b,a]中最大字串

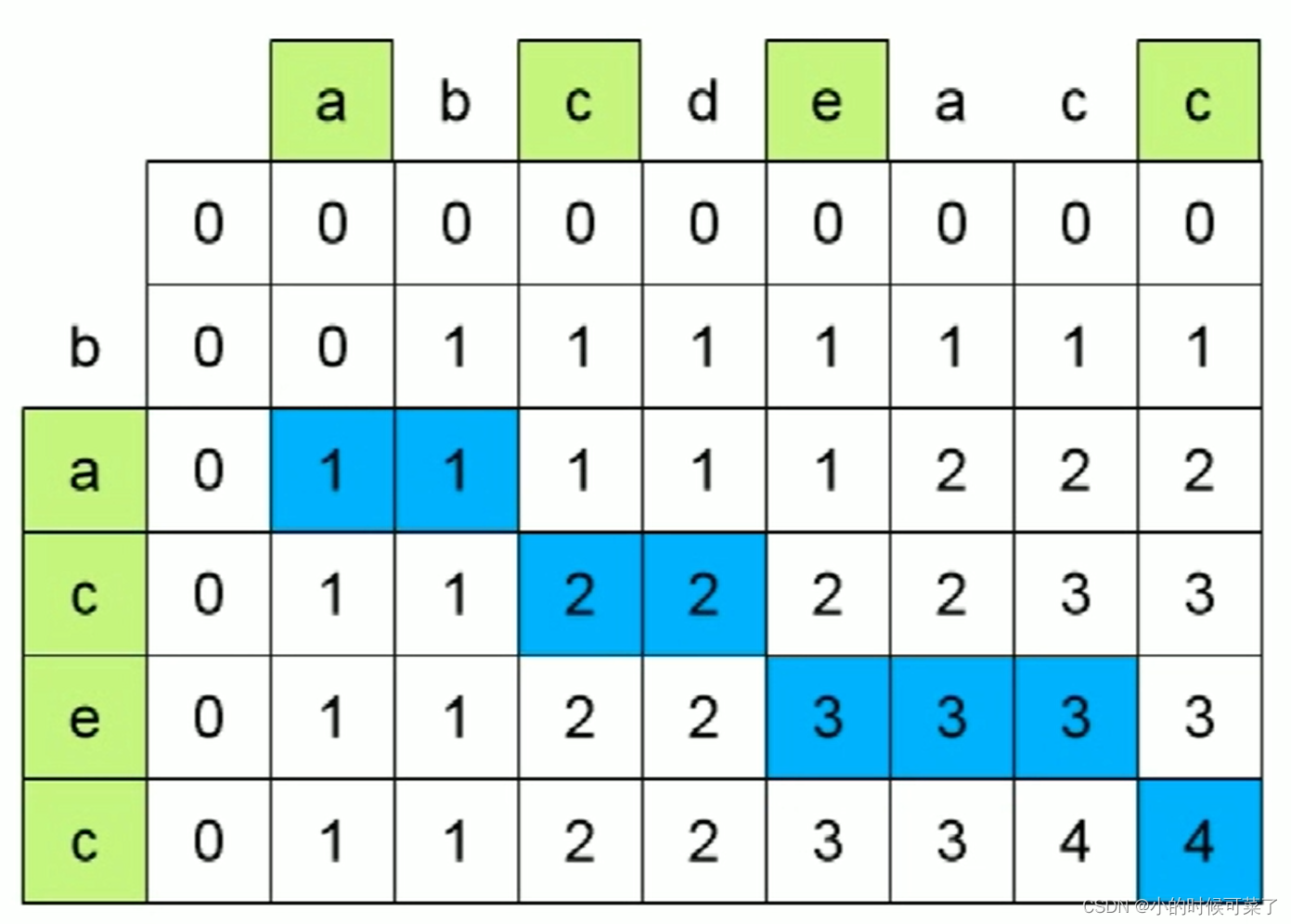
var longestCommonSubsequence = function (text1, text2) {
    let dp = new Array(text1.length + 1).fill(0).map(() =>
        new Array(text2.length + 1).fill(0)
    )
    for (let i = 1; i <= text1.length; i++) {
        dp[i][0] = 0
    }
    for (let i = 1; i <= text2.length; i++) {
        dp[0][i] = 0
    }
    for (let i = 1; i <= text1.length; i++) {
        for (let j = 1; j <= text2.length; j++) {
            if (text1[i - 1] == text2[j - 1]) {
                dp[i][j] = dp[i - 1][j - 1] + 1
            } else {
                dp[i][j] = Math.max(dp[i][j - 1], dp[i - 1][j])
            }
        }
    }
    return dp[text1.length][text2.length]
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21