推荐算法——自动特征交叉

推荐算法——自动特征交叉

目录

一、特征交叉介绍

二、特征交叉之POLY2模型--特征交叉的开始

2.1 数学模型

2.2 损失函数

2.3 梯度下降

2.4 部分代码

2.5 POLY2模型的优缺点

三、特征交叉之FM模型 —— 隐向量特征交叉

3.1 针对问题

3.2 改进思路

3.3 数学模型

3.4 损失函数

3.5 梯度下降

3.6 FM模型优点

一、特征交叉介绍

针对问题：逻辑回归存在很大的一个问题就是只对单一特征做简单加权，不具备特征交叉生成组合特征的能力，因此表达能力受到了限制。

特征交叉举例：

例子1：

        如果按照单凭每个人的个人实力去评判球队的实力，第一支球队完胜第二支球队；但我们忽略了这些球员的组合很能会导致整体实体的下降。所以对单一特征做简单加权可能会导致准确率的下滑。

例子2：

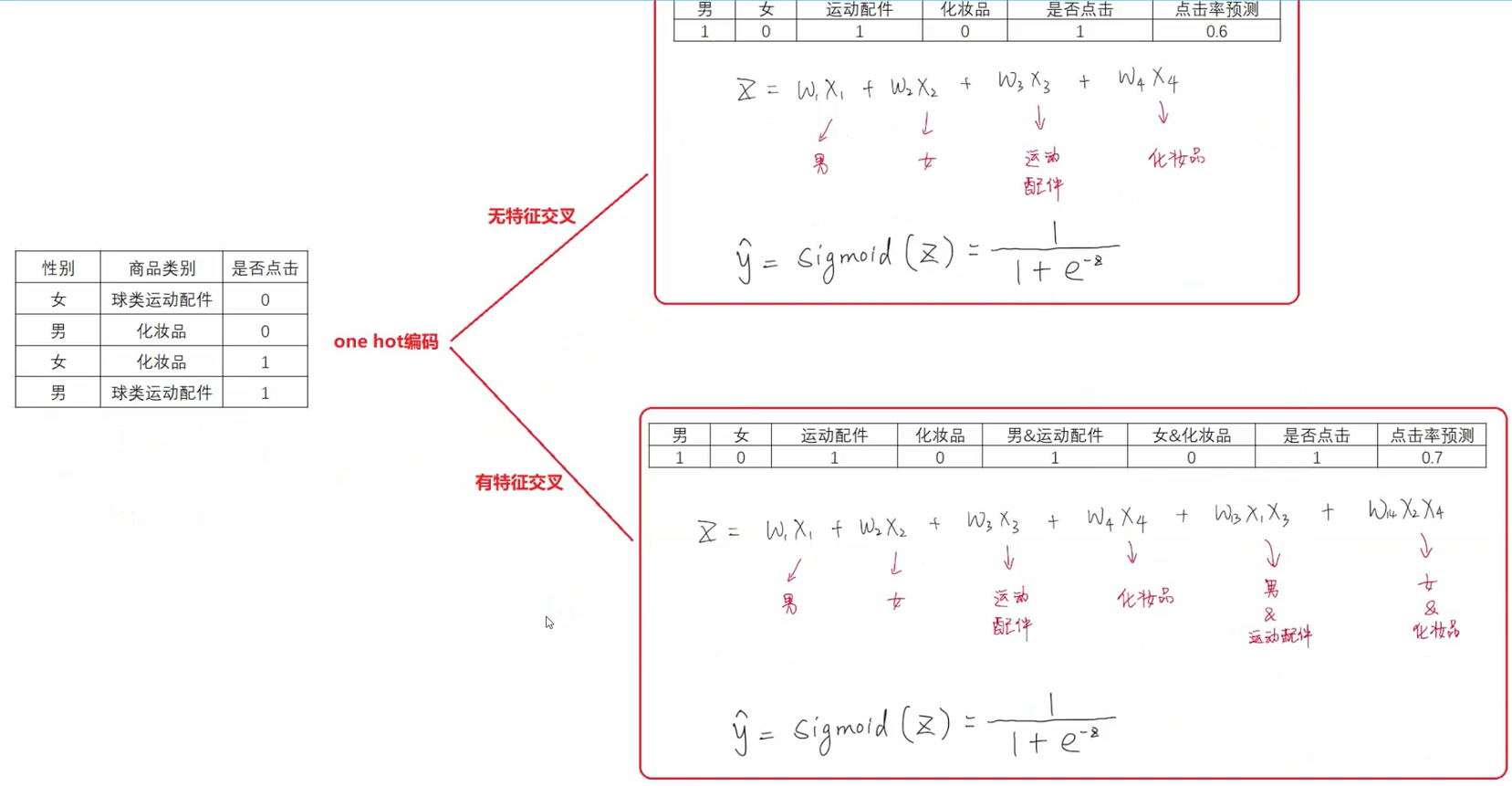
二、特征交叉之POLY2模型--特征交叉的开始

2.1 数学模型

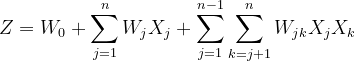
$Z=W_{0}+\sum_{j=1}^{n}W_{j}X_{j}+\sum_{j=1}^{n-1}\sum_{k=j+1}^{n}W_{jk}X_{j}X_{k}$

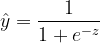
$\hat{y}=\frac{1}{1+e^{-z}}$

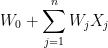$W_{0}+\sum_{j=1}^{n}W_{j}X_{j}$ 代表逻辑回归，简单的线性相加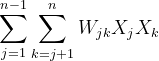； $\sum_{j=1}^{n-1}\sum_{k=j+1}^{n}W_{jk}X_{j}X_{k}$ 这部分代表特征交叉，将每个特征之间进行两两相乘并附加上权值w

物理量表示：上三角

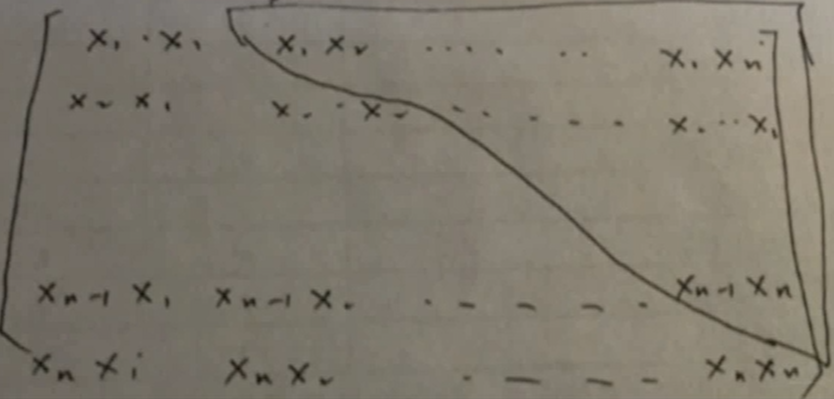
2.2 损失函数

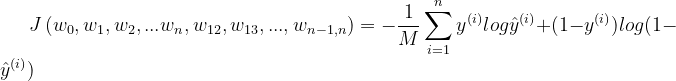
交叉熵损失： $J\left ( w_{0}, w_{1}, w_{2},... w_{n}, w_{12}, w_{13},..., w_{n-1,n}\right )=-\frac{1}{M}\sum_{i=1}^{n}y^{(i)}log\hat{y}^{(i)}+(1-y^{(i)})log(1-\hat{y}^{(i)})$

2.3 梯度下降

求梯度：

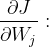
$\frac{\partial J}{\partial W_{j}}:$

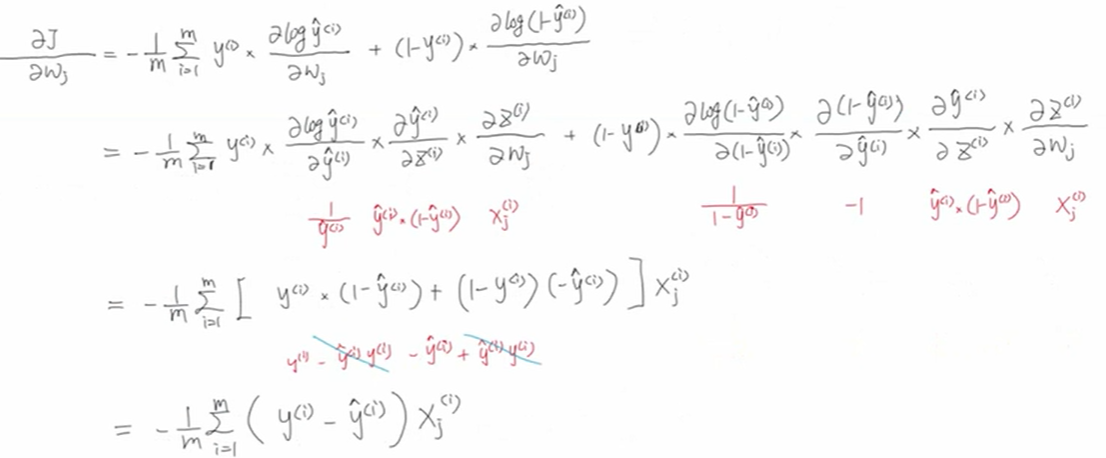
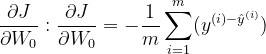
$\frac{\partial J}{\partial W_{0}}:\frac{\partial J}{\partial W_{0}}=-\frac{1}{m}\sum_{i=1}^{m}(y^{(i)-\hat{y}^{(i)}})$

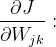
$\frac{\partial J}{\partial W_{jk}}:$

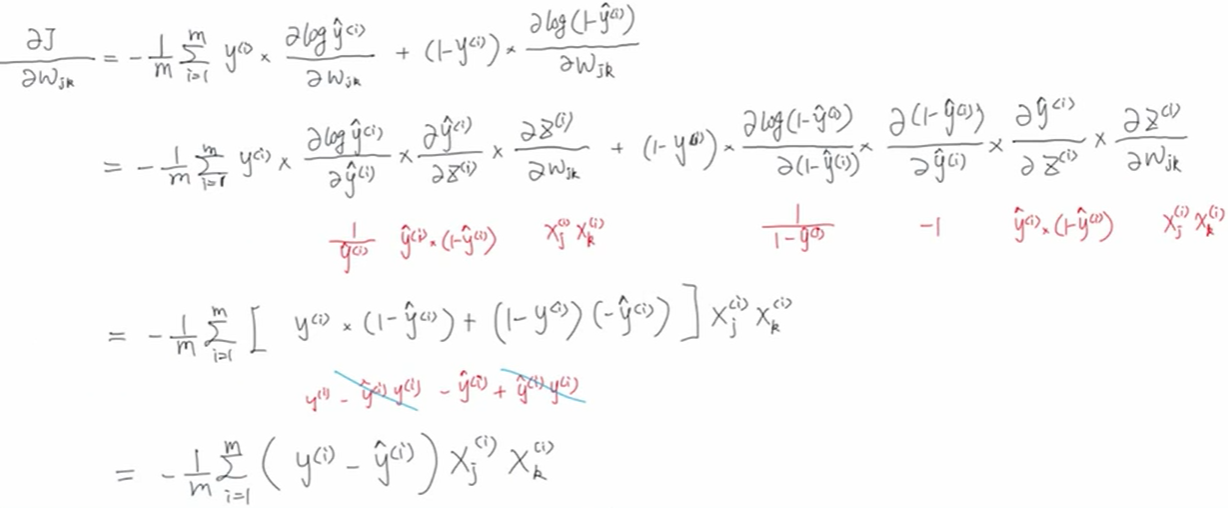
梯度更新：

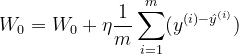
$W_{0}=W_{0}+\eta \frac{1}{m}\sum_{i=1}^{m}(y^{(i)-\hat{y}^{(i)}})$

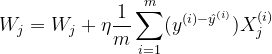
$W_{j}=W_{j}+\eta \frac{1}{m}\sum_{i=1}^{m}(y^{(i)-\hat{y}^{(i)}})X_{j}^{(i)}$

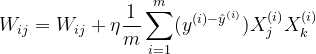
$W_{ij}=W_{ij}+\eta \frac{1}{m}\sum_{i=1}^{m}(y^{(i)-\hat{y}^{(i)}})X_{j}^{(i)}X_{k}^{(i)}$

2.4 部分代码

2.5 POLY2模型的优缺点

优点：既保留了逻辑回归的优点:充分利用用户特征、物品特征、上下文特征；一定程度上解决了特征组合的问题

缺点：1、one hot编码处理类别型数据时,会让特征向量变得极度稀疏[无选择的]特征交叉，'暴力’ 组合特征,会让原本就非常稀疏的特征向量更加稀疏；导致大部分交叉特征的权重缺乏有效的数据进行训练,无法收敛

2、训练复杂度由O(n)直接上升到O(n2)

三、特征交叉之FM模型 —— 隐向量特征交叉

传统推荐模型演化关系图：

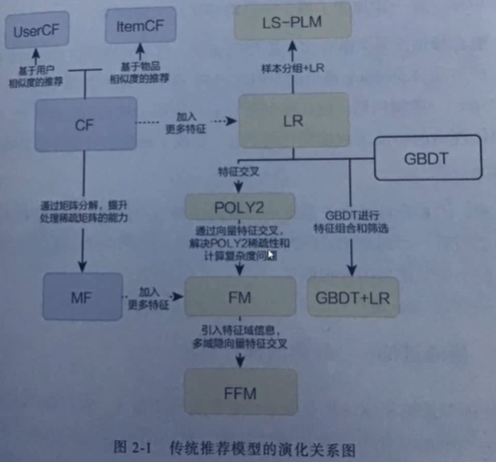
提出问题：FM模型是延续了POLY2模型的一个特征交叉的能力，由于POLY2在应对稀疏性矩阵和计算复杂度问题上是有缺陷的。当数据十分稀疏时，很多的交叉特征没有办法进行梯度下降，等到收敛，其计算复杂度为N^2，在数据量庞大时将会出现很大的问题。FM的提出就是为了解决这个问题的。

3.1 针对问题

        在面对稀疏特征向量时, POLY2特征交叉项无法收敛，POLY2计算复杂度过高。

3.2 改进思路

当k足够大时，对于任意对称正定的实矩阵W∈ 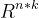$R^{n*k}$ ,均存在实矩阵V∈ 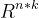$R^{n*k}$ ,使得W= $VV^{T}$

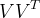
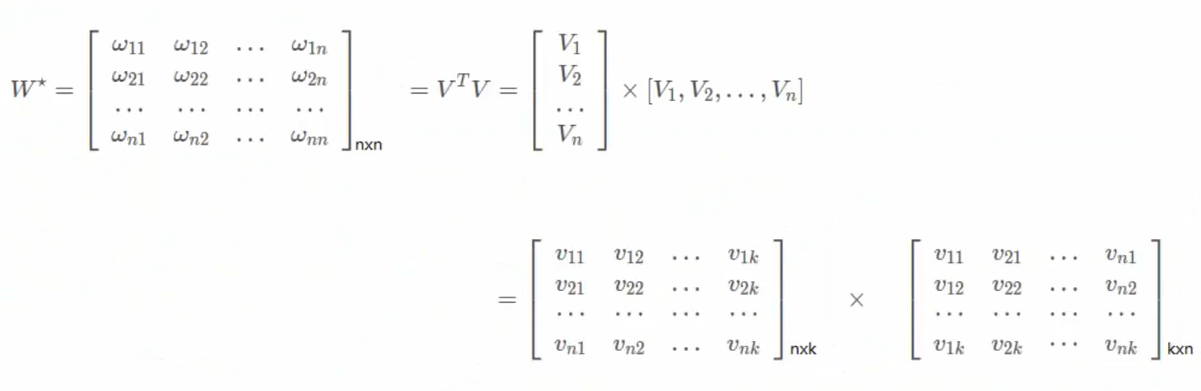
3.3 数学模型

实例：

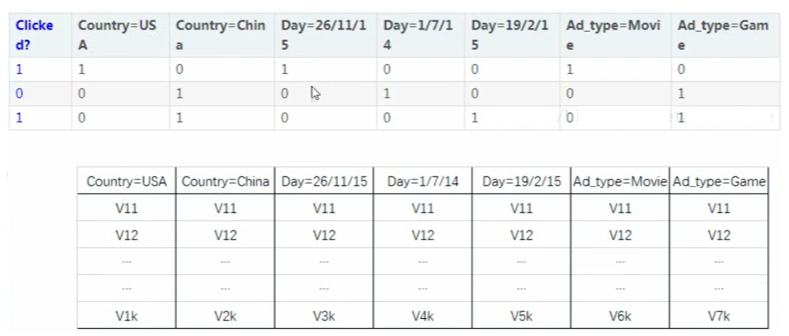         很多个特征进行热编码后，给每个特征分配一个隐向量V，当我们进行特征交叉时，不仅要对两个特征的值进行相乘，同时需要将他们对应的隐向量V进行相乘。  时间复杂度：O(kn)

3.4 损失函数

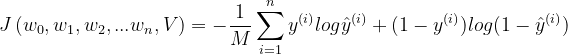
交叉熵损失： $J\left ( w_{0}, w_{1}, w_{2},... w_{n}, V\right )=-\frac{1}{M}\sum_{i=1}^{n}y^{(i)}log\hat{y}^{(i)}+(1-y^{(i)})log(1-\hat{y}^{(i)})$

3.5 梯度下降

参数： $W_{0}$ 、 $W_{i}$ 、 =

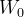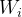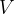公式变形：

推导过程：

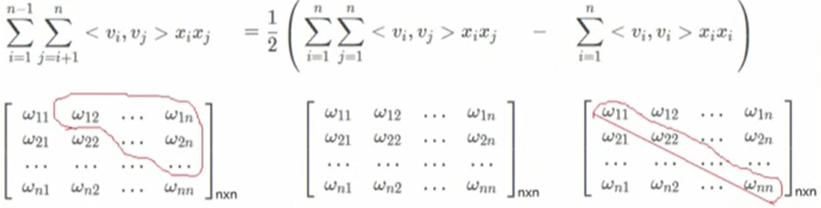
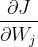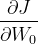
求梯度： $\frac{\partial J}{\partial W_{j}}$ 、 $\frac{\partial J}{\partial W_{0}}$

$\frac{\partial J}{\partial V_{jk}}:=-\frac{1}{m}\sum_{i=1}^{m}(y^{(i)-\hat{y}^{(i)}})\cdot \left [ x_{j}\left ( \sum_{i=1}^{n}V_{ik}\cdot x_{i} \right ) -V_{jk}x_{j}^{2}\right ]$

参数更新：

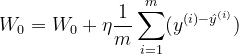
$W_{0}=W_{0}+\eta \frac{1}{m}\sum_{i=1}^{m}(y^{(i)-\hat{y}^{(i)}})$

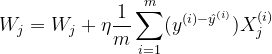
$W_{j}=W_{j}+\eta \frac{1}{m}\sum_{i=1}^{m}(y^{(i)-\hat{y}^{(i)}})X_{j}^{(i)}$

$V_{jk}=V_{jk}+\lambda \frac{1}{m}\sum_{i=1}^{m}(y^{(i)-\hat{y}^{(i)}})\cdot \left [ x_{j}^{(i)}\left ( \sum_{i=1}^{n}V_{ik}\cdot x_{i} \right ) -V_{jk}x_{j}^{2}\right ]$

3.6 FM模型优点

（1）极大降低了训练开销O(n2)一> O(kn)
（2）隐向量的引入,使得FM能更好解决数据稀疏性的问题田
（3）FM模型是利用两个特征的Embedding做内积得到二阶特征交叉的权重,那么我们可以将训练好的FM特征取出离线存好,之后用来做其他扩展
相关阅读:
List的使用
 两万字详细解读AQS，你真的了解它吗？
算法训练营第十三天 | 239. 滑动窗口最大值、347.前 K 个高频元素
 【Linux】操作系统以及虚拟机的安装与配置
 MySQL数据库——语句
 工程建设行业智能供应链系统：优化产业链运作效率，实现全链路数字化建设
 Java设计模式之单例模式(多例)、原型模式
 紫光同创FPGA实现HSSTLP高速接口通信，8b/10b编解码数据回环，提供PDS工程源码和技术支持
 C#制做一个 winform下的表情选择窗口
 牛客——OR36 链表的回文结构（C语言，配图，快慢指针）
原文地址：https://blog.csdn.net/qingxiao__123456789/article/details/125483719

一、特征交叉介绍

二、特征交叉之POLY2模型--特征交叉的开始

2.1 数学模型

2.2 损失函数

2.3 梯度下降

2.4 部分代码

2.5 POLY2模型的优缺点

三、特征交叉之FM模型 —— 隐向量特征交叉

3.1 针对问题

3.2 改进思路

3.3 数学模型

3.4 损失函数

3.5 梯度下降

3.6 FM模型优点