308. 二维区域和检索 - 可变

给你一个二维矩阵 matrix ，你需要处理下面两种类型的若干次查询：

1. 更新：更新 matrix 中某个单元的值。
2. 求和：计算矩阵 matrix 中某一矩形区域元素的 和 ，该区域由 左上角 (row1, col1) 和 右下角 (row2, col2) 界定。

实现 NumMatrix 类：

• NumMatrix(int[][] matrix) 用整数矩阵 matrix 初始化对象。
• void update(int row, int col, int val) 更新 matrix[row][col] 的值到 val 。
• int sumRegion(int row1, int col1, int row2, int col2) 返回矩阵 matrix 中指定矩形区域元素的 和 ，该区域由 左上角 (row1, col1) 和 右下角 (row2, col2) 界定。

示例 1：

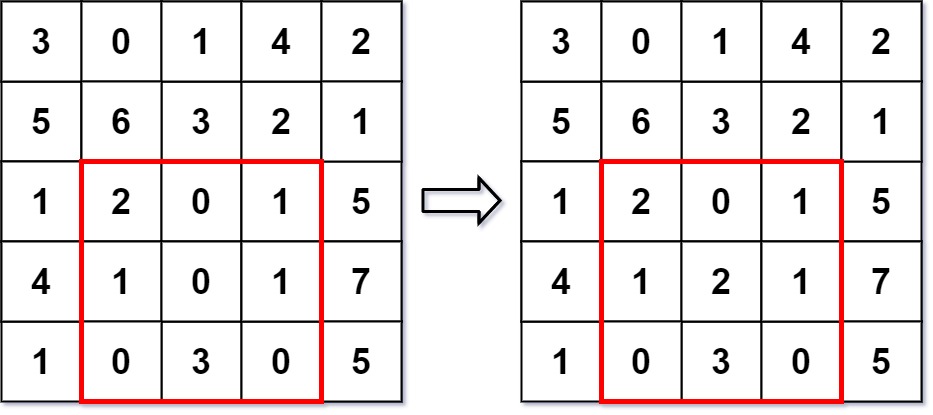
输入
["NumMatrix", "sumRegion", "update", "sumRegion"]
[[[[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]], [2, 1, 4, 3], [3, 2, 2], [2, 1, 4, 3]]
输出
[null, 8, null, 10]

解释
NumMatrix numMatrix = new NumMatrix([[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]);
numMatrix.sumRegion(2, 1, 4, 3); // 返回 8 (即, 左侧红色矩形的和)
numMatrix.update(3, 2, 2);       // 矩阵从左图变为右图
numMatrix.sumRegion(2, 1, 4, 3); // 返回 10 (即，右侧红色矩形的和)

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 200
• -10^5 <= matrix[i][j] <= 10^5
• 0 <= row < m
• 0 <= col < n
• -10^5 <= val <= 10^5
• 0 <= row1 <= row2 < m
• 0 <= col1 <= col2 < n
• 最多调用10^4 次 sumRegion 和 update 方法

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/range-sum-query-2d-mutable
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

做题结果

成功，用了两种解法

方法1：哈希

懒加载的二维前缀和，好处是一直update或一直求和，复杂度还是O(1)，交替时是 O(mn)

1. 初始化前缀和

2. 更新数据时，标记

3.  获取有标记时，更新数组，去除标记

class NumMatrix {
        int[][] arr;
        int[][] pre;
        int m;
        int n;
        boolean hasChange;
        public NumMatrix(int[][] matrix) {
            arr = matrix;//改前缀和。。。
            m = matrix.length;
            n = matrix[0].length;
            pre = new int[m+1][n+1];
            for(int i = 0; i<m; i++){
                for(int j = 0; j < n; j++){
                    pre[i+1][j+1]=matrix[i][j]+pre[i][j+1]+pre[i+1][j]-pre[i][j];
                }
            }
        }
 
        public void update(int row, int col, int val) {
            arr[row][col] = val;
            hasChange = true;
        }
 
        public int sumRegion(int row1, int col1, int row2, int col2) {
            if(hasChange){
                for(int i = 0; i<m; i++){
                    for(int j = 0; j < n; j++){
                         pre[i+1][j+1]=arr[i][j]+pre[i][j+1]+pre[i+1][j]-pre[i][j];
                    }
                }
                hasChange = false;
            }
 
            return pre[row2+1][col2+1]+pre[row1][col1]-pre[row1][col2+1]-pre[row2+1][col1];
        }
    }

方法2：线段树 

这题其实是二维线段树，记录左上角和右下角，共四个点

1. 建立线段树，共四个点，一个和，两个孩子

2. 递归分配孩子时，优先分行，再分列【方便，一次分四个也可以，需要判断的会多一点】

3. 算出孩子的值，逐一往上递推，拿到整体前缀和

4. 添加元素：不在范围内返回，在范围内递推添加，传递到孩子

5. 求和： 当前范围值，都在目标范围内直接返回sum；都不在目标内直接返回0；否则累计孩子的和

class NumMatrix {
        SquareTree tree;
        int[][] arr;
        public NumMatrix(int[][] matrix) {
            arr = matrix;
            tree = new SquareTree(0,0,matrix.length-1,matrix[0].length-1,matrix);
        }
 
        public void update(int row, int col, int val) {
            int diff = val-arr[row][col];
            arr[row][col] = val;
            tree.add(row,col,diff);
        }
 
        public int sumRegion(int row1, int col1, int row2, int col2) {
            return tree.getSum(row1,col1,row2,col2);
        }
    }
 
class SquareTree{
    int x1;
    int x2;
    int y1;
    int y2;
    int sum;
    SquareTree t1;
    SquareTree t2;
    public SquareTree(int x1, int y1, int x2, int y2,int[][] arr){
        this.x1 = x1;
        this.y1 = y1;
        this.x2 = x2;
        this.y2 = y2;
        sum = initSum(x1,y1,x2,y2,arr);
    }
 
    private int initSum(int X1, int Y1, int X2, int Y2, int[][] arr){
        if(X1==X2 && Y1 == Y2){
            sum = arr[X1][Y1];
            return sum;
        }
        if(x1<x2){
            int mid = (x2-x1)/2+x1;
            t1 = new SquareTree(x1,y1,mid,y2,arr);
            t2 = new SquareTree(mid+1,y1,x2,y2,arr);
        }else{
            int mid = (y2-y1)/2+y1;
            t1 = new SquareTree(x1,y1,x2,mid,arr);
            t2 = new SquareTree(x1,mid+1,x2,y2,arr);
        }
 
        sum = t1.sum+t2.sum;
        return sum;
    }
 
    public void add(int x, int y,int v){
        if(x<x1||x>x2||y<y1||y>y2){
            return;
        }
        sum += v;
        if(t1!=null)
            t1.add(x,y,v);
        if(t2!=null)
            t2.add(x,y,v);
    }
 
 
 
    public int getSum(int X1, int Y1, int X2, int Y2){
        if(x2<X1||x1>X2||y2<Y1||y1>Y2){
            return 0;
        }
        //都在范围里
        if(X1<=x1&&X2>=x2&&Y1<=y1&&Y2>=y2){
            return sum;
        }
 
        return t1.getSum(X1,Y1,X2,Y2)+t2.getSum(X1,Y1,X2,Y2);
    }
 
}