前言

Hello！
非常感谢您阅读海轰的文章，倘若文中有错误的地方，欢迎您指出～
 
自我介绍 ଘ(੭ˊᵕˋ)੭
昵称：海轰
标签：程序猿｜C++选手｜学生
简介：因C语言结识编程，随后转入计算机专业，获得过国家奖学金，有幸在竞赛中拿过一些国奖、省奖…已保研。
学习经验：扎实基础 + 多做笔记 + 多敲代码 + 多思考 + 学好英语！
 
唯有努力💪
 

知其然 知其所以然！

 
本文仅记录自己感兴趣的内容

ABSTRACT

现有的网络嵌入方法几乎都采用浅模型（ shallow models）

然而，由于底层网络结构复杂，浅层模型无法捕捉到高度非线性的网络结构，导致网络表达次优

因此，如何找到一种能够有效捕捉高度非线性网络结构并保持全局和局部结构的方法是一个开放而重要的问题

---

为了解决这一问题，本文提出了一种结构化深度网络嵌入方法，即SDNE。

更具体地说，我们首先提出了一个半监督深度模型，该模型具有多层非线性函数，从而能够捕捉高度非线性的网络结构。

然后我们提出利用一阶和二阶邻近性来保护网络结构。

• 无监督分量利用二阶邻近性来捕捉全局网络结构
• 而在监督分量中使用一阶邻近度作为监督信息，以保持局部网络结构

通过在半监督深度模型中对它们进行联合优化，该方法

• 既能保持局部网络结构
• 又能保持全局网络结构
• 对稀疏网络具有鲁棒性

1. INTRODUCTION

如今，网络无处不在，许多真实世界的应用程序需要挖掘这些网络中的信息

例如

• Twitter的推荐系统旨在挖掘社交网络中用户的首选推文
• 在线广告定位往往需要将用户聚集到社交网络中的社区中

因此，对网络中的信息进行挖掘是非常重要的。其中一个基本问题是如何学习有用的网络表示[5]

一种有效的方法是将网络嵌入到低维空间中，即学习每个顶点的向量表示，目的是在学习到的嵌入空间中重建网络

因此，可以直接在低维空间中对网络中的信息进行挖掘，如信息检索[34]、分类[15]、聚类[20]等

---

学习网络表示面临以下挑战:

• (1)高度非线性: 正如[19]所说，网络的底层结构是高度非线性的。因此，如何设计一个模型来捕捉高度非线性的结构是相当困难的。

• (2)保留结构:为了支持应用分析网络，需要网络嵌入来保留网络结构。然而，网络的底层结构是非常复杂的[24]。顶点的相似性取决于局部和全局网络结构。因此，如何同时保护局部和全局结构是一个棘手的问题。

• (3)稀疏性:许多现实世界的网络往往是如此稀疏，仅利用非常有限的观察链接不足以达到令人满意的性能

---

在过去的几十年里，人们提出了许多采用浅层模型的网络嵌入方法，如IsoMAP[29]、Laplacian Eigenmaps (LE)[1]和Line[26]

然而，由于浅层模型[2]的表达能力有限，很难捕捉到高度非线性的网络结构[30]

虽然有些方法采用了内核技术[32]，但正如[36]所述，内核方法也是浅层模型，不能很好地捕捉高度非线性的结构。

---

为了更好地捕捉网络的高度非线性结构，本文提出了一种新的深度模型来学习网络顶点表示

在我们提出的模型中，我们设计了一个由多个非线性函数组成的多层结构

多层非线性函数的组合可以将数据映射到一个高度非线性的潜在空间，从而能够捕捉到高度非线性的网络结构

---

为了解决深度模型的结构保持和稀疏性问题，我们进一步提出在学习过程中联合利用一阶和二阶接近[26]

一阶邻近性是指仅由边连接的顶点之间的局部两两相似度，它表征了局部网络结构

然而，由于网络的稀疏性，许多合法的链接丢失了。因此，一阶接近度不足以表示网络结构

因此，我们进一步提出了二阶邻近性，它表明顶点的邻域结构的相似性，以获取全局网络结构

通过一阶和二阶近似，我们可以分别很好地刻画局部和全局网络结构

---

为了在深度模型中同时保留局部和全局网络结构，我们提出了一种半监督结构

• 其中无监督分量重构二阶邻近性来保留全局网络结构
• 监督分量利用一阶邻近性作为监督信息来保留局部网络结构

学习后的表示可以很好地保留局部和全局网络结构。

如图1所示，二阶接近的顶点对的数量要比一阶接近的顶点对的数量大得多

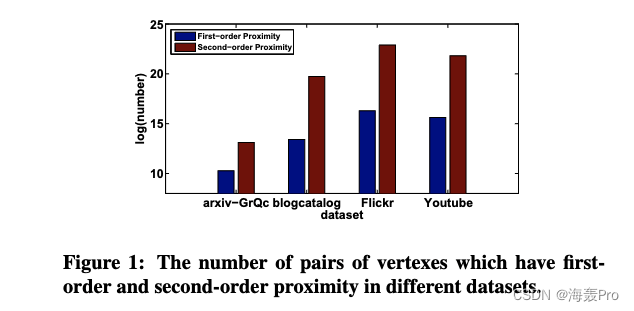
图1：在不同数据集中具有一阶和二阶接近性的顶点对的数量。

---

本文的贡献如下:

• 我们提出一种结构化深度网络嵌入方法(SDNE)来实现网络嵌入。该方法能够将数据映射到一个高度非线性的潜在空间，以保持网络结构，并对稀疏网络具有鲁棒性。据我们所知，我们是最早使用深度学习来学习网络表征的文章之一。
• 我们提出了一种新的半监督结构的深度模型，它同时优化了一阶和二阶邻近性。因此，学习到的表示保持了局部和全局网络结构，对稀疏网络具有鲁棒性。
• 该方法在5个真实数据集和4个应用场景上进行了广泛的评估。实验结果表明，该方法在多标签分类、重构、链接预测和可视化等方面具有较好的实用性。具体来说，当标记数据稀缺时，我们的方法可以实现比基线更显著的改进(20%)。在某些情况下，我们只需要减少60%的训练样本，但仍然可以获得更好的性能。

2. RELATED WORK

2.1 Deep Neural Network

表征学习一直是机器学习的一个重要问题，许多研究都是针对样本的表征学习[3,35]

深度神经网络的最新进展表明，它们具有强大的表示能力[12]，可以为许多类型的数据生成非常有用的表示

例如：

• [15]提出了一种七层卷积神经网络来生成用于分类的图像表示
• [33]提出了一种学习图像-文本统一表示的多模态深度模型，以实现跨模态检索任务。

然而，据我们所知，很少有深度学习工作处理网络，特别是学习网络表示

• 在[9]中，采用限制玻尔兹曼机进行协同过滤
• [30]采用深度自编码器对图进行聚类
• [5]提出了一个异构深度模型来实现异构数据嵌入

我们与这些作品有两个不同之处。

• 首先，目标不同。我们的工作重点是学习低维结构保留的网络表示，可以在任务之间使用
• 其次，我们同时考虑顶点之间的一阶和二阶邻近性，以保持局部和全局网络结构。但它们只关注一阶信息

2.2 Network Embedding

我们的工作解决了网络嵌入的问题，其目的是学习网络的表示。

较早的作品如LLE (Local Linear Embedding)[22]、IsoMAP[29]等首先基于特征向量构造亲和图，然后求解主导特征向量作为网络表示。

最近

• [26]设计了两个损失函数，分别试图捕获局部和全局网络结构。
• [4]扩展了利用高阶信息的工作

尽管这些网络嵌入方法都取得了成功，但它们都采用了浅层模型。

---

正如我们前面所解释的，浅层模型很难有效地捕捉底层网络中的高度非线性结构。

此外，尽管他们中的一些人试图使用一阶和高阶接近来保留局部和全局网络结构，但他们分别学习它们的表示，并简单地串联这些表示。

显然，与同时在一个统一的体系结构中建模以获取局部和全局网络结构相比，它是次优的

DeepWalk[21]结合了random walk和skip-gram来学习网络表示虽然在经验上是有效的

• 但它缺乏一个明确的目标函数来阐明如何保存网络结构
• 它倾向于只保留二阶接近。

然而，我们的方法设计了一个明确的目标函数，目的是通过保持一阶和二阶的接近性来同时保持局部和全局结构。

3. STRUCTURAL DEEP NETWORK EMBEDDING

3.1 Problem Definition

DEFINITION 1.

• $G=(V,E)$
• 权重：$s_{i,j}$
  • 无权图：$v_i$与$v_j$之间有边，$s_{i,j}=1$，没有边，$s_{i,j}=0$
  • 有权图:$v_i$与$v_j$之间有边，$s_{i,j}$为权重，没有边，$s_{i,j}=0$

---

DEFINITION 2.

First-Order Proximity:一阶接近描述顶点之间的两两接近

对于任意顶点对

• 如果$s_{i,j}>0$, 则$v_i$和$v_j$之间存在正的一阶接近
• 否则，$v_i$与$v_j$的一阶接近度为0。

---

DEFINITION 3.

Second-Order Proximity:两个顶点之间的二阶邻近性描述了两个顶点的邻域结构的邻近性

令 N u = { s u , 1 ， … ， s u ， ∣ V ∣ } N_u = \{s_{u,1}，…， s_{u，|V|}\} Nu​={su,1​，…，su，∣V∣​}表示$v_u$与其他顶点的一阶接近

然后，二阶接近度由$N_u$和$N_v$的相似度决定

---

DEFINITION 4.

Network Embedding：给定图$G=(V,E)$，网络嵌入的目的是学习一个映射函数$f:v_i\to y_i\in R^d$，其中$d<<|V|$

该函数的目的是使$y_i$和$y_j$之间的相似性显式地保持$v_i$和$v_j$的一阶和二阶接近

3.2 The Model

3.2.1 Framework

SDNE框架如图2所示

---

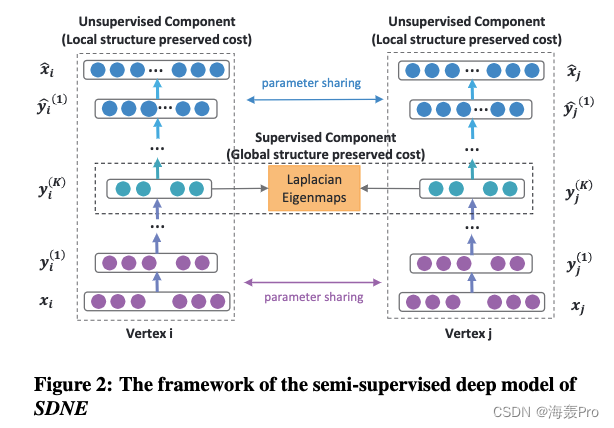
为了捕获高度非线性的网络结构

• 提出了一种深度架构，该架构由多个非线性映射函数组成，将输入数据映射到一个高度非线性的潜在空间，以捕获网络结构

为了解决结构保持和稀疏性问题

• 提出了一个半监督模型，利用二阶和一阶接近

对于每个顶点，我们可以获得它的邻域。因此，我们设计了无监督分量，通过重建每个顶点的邻域结构来保持二阶邻近性

同时，对于一小部分节点对，我们可以得到它们的成对相似性，即一阶近邻。

因此，我们设计监督组件来利用一阶邻近性作为监督信息来细化潜在空间中的表示。

通过在半监督深度模型中对它们进行联合优化，SDNE可以很好地保持高度非线性的局部-全局网络结构，对稀疏网络具有鲁棒性。

3.2.2 Loss Functions

一些术语和符号

注意，参数上面的$ˆ$表示解码器的参数。

---

我们首先描述无监督组件如何利用二阶邻近性来保持全局网络结构

二阶邻近性是指一对顶点的邻域结构有多相似

因此，要对二阶邻近度进行建模，就需要对每个顶点的邻域进行建模

1. 给定一个网络$G=(V,E)$，我们可以得到它的邻接矩阵$S$，它包含$n$个实例$s_1，\dots ,s_n$

2. 对于每个实例 s i = { s i , j } j = 1 n , s i , j > 0 s_i = \{s_{i,j}\}^n_{j=1}, s_{i,j} > 0 si​={si,j​}j=1n​,si,j​>0当且仅当$v_i$和$v_j$之间存在连接

3. 因此，$s_i$描述了顶点$v_i$的邻域结构，$S$提供了每个顶点的邻域结构信息

利用$S$，我们扩展了传统的深度自编码器[23]，以保持二阶邻近性

---

考虑到深度自编码器的独立性，我们简要回顾了深度自编码器的关键思想

它是一个无监督模型，由编码器和解码器两部分组成。

• 编码器由多个非线性函数组成，它们将输入数据映射到表示空间

• 解码器还包含多个非线性函数，将表示空间中的表示映射到重构空间

然后给定输入$x_i$，每层的隐藏表示如下2所示

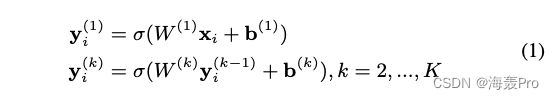
得到$y_i^{(K)}$后，反转编码器的计算过程，得到输出${\hat{x}}_i$。

自动编码器的目标是使输出和输入的重构误差最小化。损失函数如下所示:

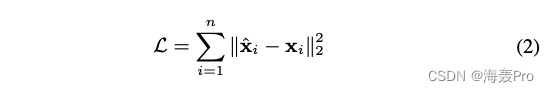
[23]证明，虽然最小化重构损失并不能显式地保持样本之间的相似性，但重构准则可以平滑地捕获数据流形，从而保持样本之间的相似性

---

然后考虑到我们的情况，如果我们用邻接矩阵S作为自编码器的输入，即$x_i=s_i$

由于每个实例$s_i$表征了顶点$v_i$的邻域结构，重建过程将使具有相似邻域结构的顶点具有相似的潜在表示

然而，由于网络的某些特定特性，这样的重构过程并不能直接应用于我们的问题

在网络中

• 我们可以观察到一些链接，但同时却看不到许多合法的链接，这意味着顶点之间的链接确实表明了它们的相似性，但没有链接并不一定表明它们的不同。
• 此外，由于网络的稀疏性，S中非零元素的数量远小于零元素的数量。

那么如果我们直接使用S作为传统自动编码器的输入，它更容易重构S中的零元素。然而，这并不是我们想要的。

为了解决这一问题，我们对非零元素的重构误差施加了比零元素重构误差更大的惩罚。修正后的目标函数如下:

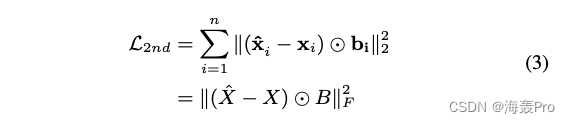
其中$\odot$表示哈达玛积(Hadamard product)
b i = { b i , j } j = 1 n = { b i , j = 1 s i , j = 1 b i , j = β > 1 e l s e b_i = \{b_{i,j}\}^n_{j=1}={bi,j=1si,j=1bi,j=β>1else

bi​={bi,j​}j=1n​={bi,j​=1si,j​=1bi,j​=β>1else​

现在，通过使用以邻接矩阵$S$为输入的修正深度自编码器，将具有相似邻域结构的顶点映射到表示空间的附近，并由重构准则保证。

再原来的基础上 ，对非零元素施加更大的惩罚，修正损失函数

换句话说，我们的模型的无监督组件可以通过重建顶点之间的二阶邻近性来保持全局网络结构。

通过使用修正后深度自编码器在保持二阶邻近性

---

不仅要保护全局网络结构，而且要抓住局部结构。

我们用第一接近度来表示局域网络结构

一阶接近度可以看作是约束一对顶点潜在表示相似度的监督信息。

因此，我们设计监督组件利用一阶接近。这个目标的损失函数定义如下3

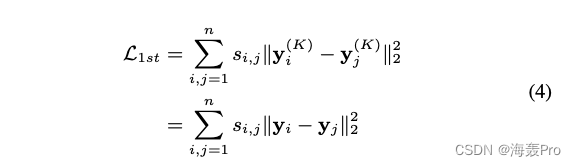
公式4的目标函数借用了拉普拉斯特征映射[1]的思想

• 当相似顶点在嵌入空间的远处映射时，会产生一个惩罚
• 一些关于社交网络[13]的作品也使用了类似的想法
• 我们在深度模型中引入了这种思想，使由边连接的顶点在嵌入空间中被映射到附近
• 因此，该模型保持了一阶接近。

---

为了同时保持一阶和二阶的接近性，我们提出了一个半监督模型，最小化以下目标函数:

其中$L_{reg}$是防止过拟合的$L2$范数正则化项，其定义如下:

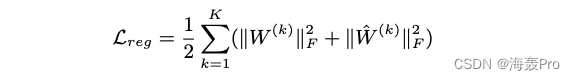
3.2.3 Optimization

通过对参数进行初始化，利用随机梯度下降法对深度模型进行优化

需要注意的是，由于模型的高非线性，它在参数空间中会有许多局部最优

因此，为了找到一个好的参数空间区域，我们首先使用Deep Belief Network在[11]处对参数进行预训练，这在文献[7]中已经被证明是深度学习的一个必要的参数初始化。

完整的算法步骤如下：

3.3 Analysis and Discussions

New vertexes

网络嵌入的一个实际问题是如何学习新到达顶点的表示

对于新顶点的表示是一个问题

1） 对于一个新顶点$v_k$，如果已知它与现有顶点的连接

• 我们可以得到它的邻接向量 x = { s 1 , k ， … ， s n , k } x = \{s_{1,k}，…， s_{n,k}\} x={s1,k​，…，sn,k​}，其中$s_{i,k}$表示已有顶点$v_i$与新顶点$v_k$的相似度

• 然后我们可以简单地将$x$输入到我们的深度模型中，并使用训练好的参数$\theta$来得到$v_k$的表示。该过程的复杂度为$O(1)$

2）如果$v_i$和网络中现有的顶点之间不存在连接

• 我们的方法和最先进的网络嵌入方法无法处理。
• 对于这种情况，我们可以求助于其他方面的信息，比如新顶点的内容特征，我们留给以后的工作

---

Training Complexity

模型的训练复杂度为$O(ncdI)$

• 其中$n$为顶点数
• $d$为隐藏层的最大维数，通常与嵌入向量的维数有关，而与顶点的个数n无关。
• $c$为网络的平均度，在实际应用中，它通常可以被视为一个常数
• $I$为迭代次数，与n无关

整体训练复杂度与网络中的顶点数量成线性关系

4. EXPERIMENTS

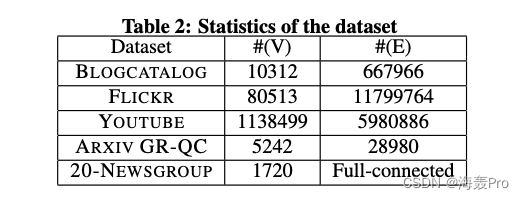
4.1 Datasets

• BLOGCATALOG [27], FLICKR [27] and YOUTUBE [28]
• ARXIV GR-QC
• 20-NEWSGROUP

4.2 Baseline Algorithms

• DeepWalk
• LINE
• GraRep
• Laplacian Eigenmaps (LE)
• Common Neighbor

4.3 Evaluation Metrics

在我们的实验中，我们完成了重建、链接预测、多标签分类和可视化的任务。

对于重建和链路预测，我们使用precision@k和平均精度(Mean Average Precision, MAP)来评估性能。它们的定义如下:

对于多标签分类任务，我们采用了$Micro-F1$和$Macro-F1$的定义如下

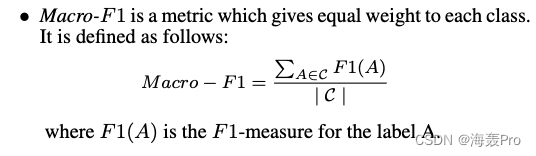
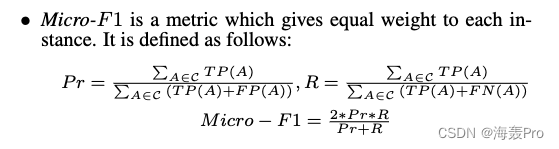
4.4 Parameter Settings

本文提出了一种多层深度结构，层数随数据集的不同而不同。

各层的维度如表3所示

• 神经网络有三层用于BLOGCATALOG、ARXIV GR-QC和20-NEWSGROUP
• 四层用于FLICKR和YOUTUBE

如果我们使用更深层次的模型，性能几乎保持不变，甚至变得更差。

4.5 Experiment Results

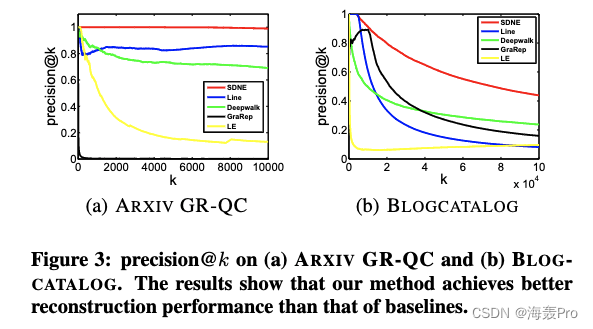
4.5.1 Network Reconstruction

图3显示了precision@k上的结果

MAP的结果如表4所示

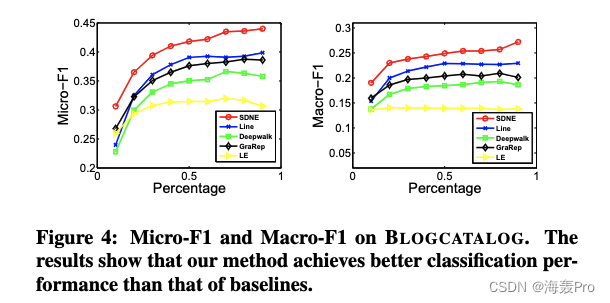
4.5.2 Multi-label Classification

4.5.3 Link Prediction

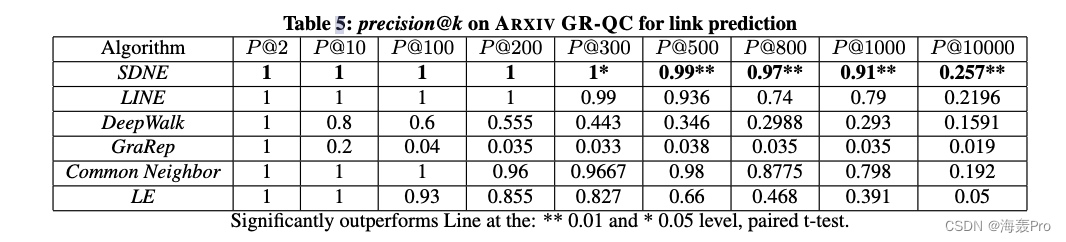
4.5.4 Visualization

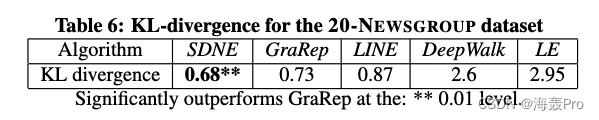
可视化图如图7所示

我们使用Kullback-Leibler散度作为定量评价指标

• KL散度越低，性能越好

结果如表6所示

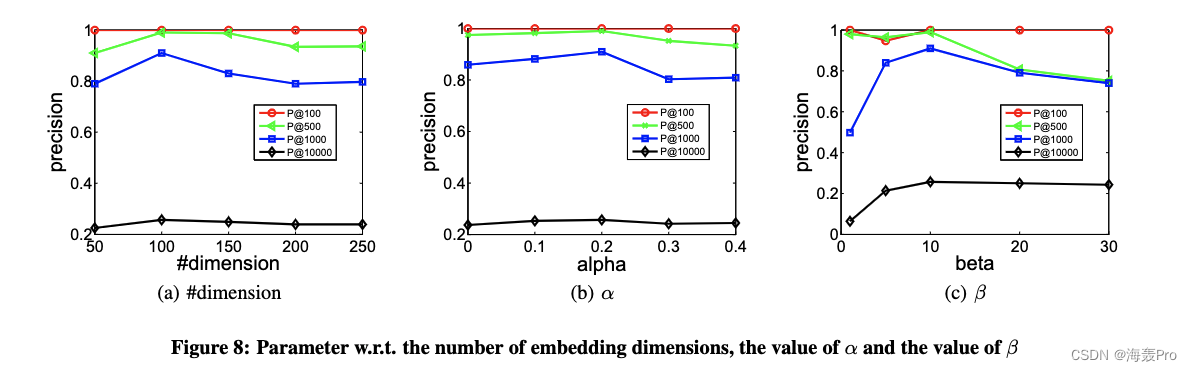
4.6 Parameter Sensitivity

评估了不同的嵌入维数和不同的超参数α和β值对结果的影响

• $L_{2nd}$含有超参数$\beta$
• $L_{1st}$含有超参数$\alpha$

读后总结

总目标优化函数

其中

• $L_{2nd}$是利用自编码器对输入输出的一个损失计算（这里是修改了一下损失函数，是无监督的）
• $L_{1st}$是对自编码器中每一个隐层中对应的$y_i$与其余节点对应的$y_j$的损失计算（借助拉普拉斯特征映射的思想，是监督的）
• $L_{reg}$是为了防止过拟合引入的一个损失计算

总体思路不是很难，利用编码器，依据重构损失和其中隐层变量的损失构成最终的目标函数

寻找到最优参数即可

结语

文章仅作为个人学习笔记记录，记录从0到1的一个过程

希望对您有一点点帮助，如有错误欢迎小伙伴指正