【学习笔记】最短路 +生成树

困难的题目

Opening Portals

好题！

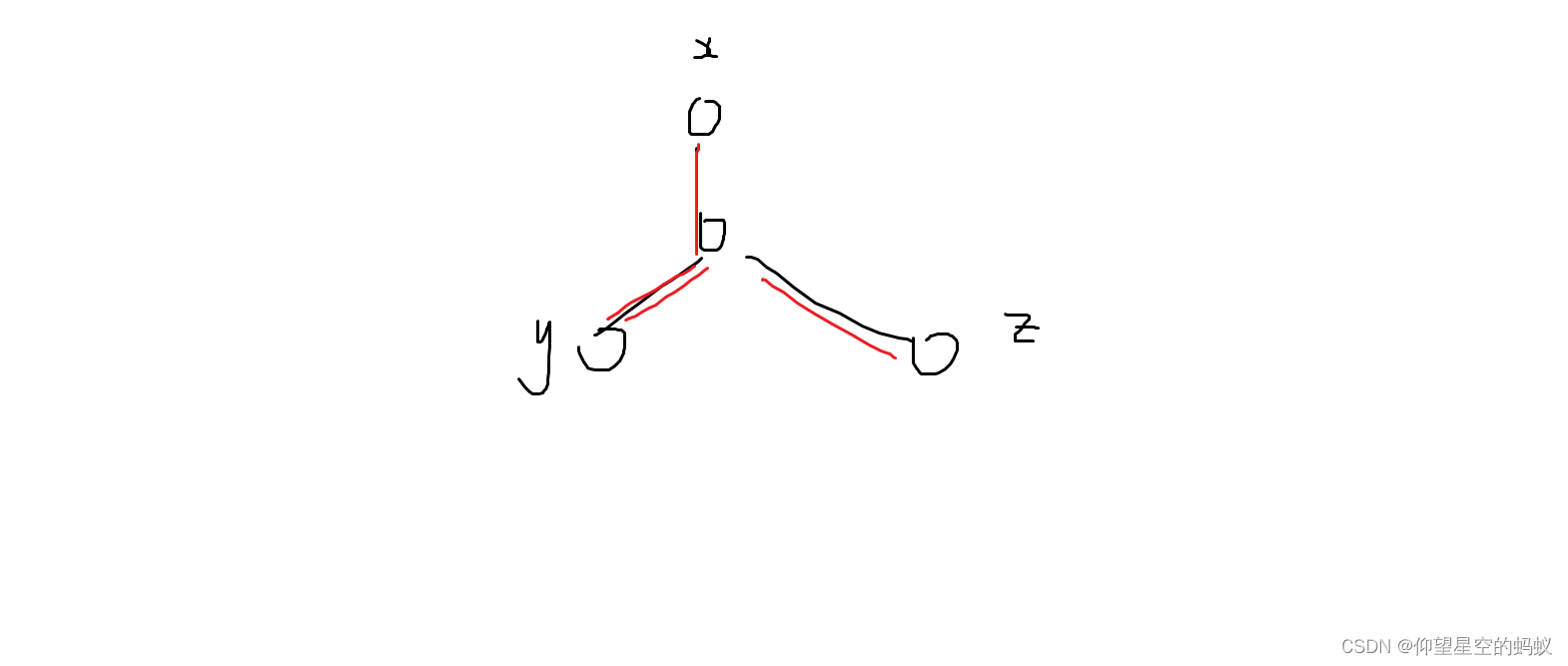
我们称传送门为关键点。

设任意两个关键点之间距离为 dist(i,j) ，考虑到传送的性质，只需求出一个连接所有关键点的生成树，然后从任意一个关键点出发遍历，恰好为生成树的边权和。（有点绕）

如果我们以每个关键点为起点跑 dijkstra ， 时间复杂度为 $O(n^2\log n)$ 。

对于这个模型，我们有一个 多源最短路 算法 ：

1. 以每个关键点为起点，求出到每个点的最短距离
2. 考虑枚举一条边 (u,v,w) ，将距这条边两个端点最近的两个关键点连起来：（相当于枚举中转点）

正确性是显然的。

特别地，MST 就是每个点都是关键点的情况 。

当然，一条边可能会在生成树上被计算多次。

Complete the MST

这题不需要高深算法。直接莽

可以直接跑完全图 MST ，然后找次小生成树 （分讨即可） 。

Jumping Around

boruvka 板题

Trial for Chief

好精巧的小构造！

万万没想到是最短路 ！

考虑从 (i,j) 出发，相邻的颜色不同的格子距离为 1 ，颜色相同的格子距离为 0 ，找到距离最远的黑色格子，答案为 dist+1 。（特判全白）

考虑它的意义。相当于黑白交替，贪心地操作。

Flights

咕咕咕。。。

差分约束 + 最短路 ！！

Capitalism

妙题 ！

首先判断奇环一定无解。

这题的图很特殊，因为是双向边，所以从连通块的任意一点出发都能到达其他点 。因此我们枚举 S 作为起点，跑差分约束。

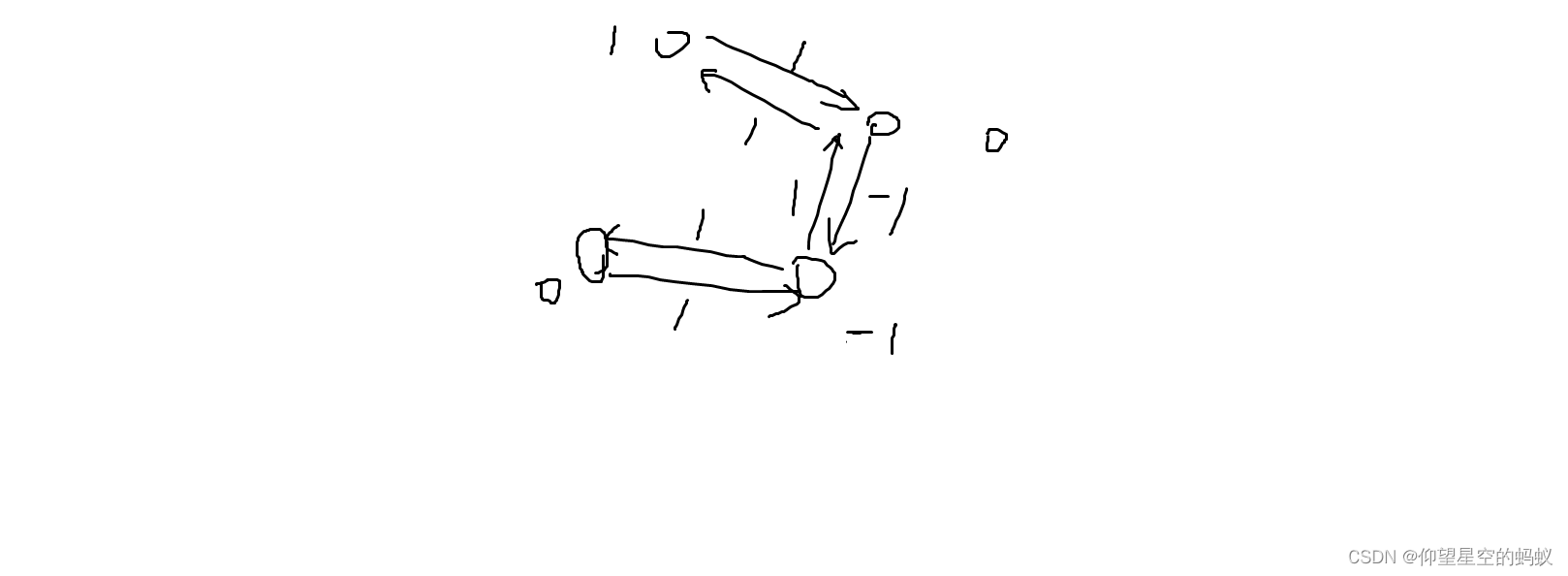
很巧的地方在于不会出现有边连的 dis[u]=dis[v] 的情况，否则会出现奇环。

这样可以得到一组合法的解。

然后要满足极差最大 。

不能建超级原点 。qwq