-
数据结构——线性表
1.引言
最近考研正式进入到了408阶段,大致时间线上还算正常。由于王道课本里面的算法题实在是太经典了,而且书写的代码质量比较高,如果是仅仅看书的话显然是不够的,而且容易犯困,自己其实基础也不太好,只是喜欢捣鼓一些非底层的东西😥。因此决定面向CSDN博客学习😏,让学习更加趣味化🐲,提高自己学习深度🌱 ,分享的同时督促自己真正理解这些难啃的算法题。你可能想知道的CSDN图标😲。温馨提示,本文代码较多,主要是为了方便自己之后复习,多多见谅。
2.线性表的基本组成
这里直接放一张线性表的结构图:

3.顺序表的基本操作
顺序表指的是用一系列连续的存储单元来存储线性表中的元素,使得逻辑相邻的元素在位置上也是相邻的。给出代码示例:
(1)顺序表结构定义:#define MaxSize 50 typedef int ElemType; typedef struct { ElemType data[MaxSize]; int length; } SqlList;- 1
- 2
- 3
- 4
- 5
- 6
(2)顺序表初始化:
/** * @brief 初始化线性表 * * @param L 线性表 */ void initSqlList(SqlList* L) { L->length = 0; cout << "初始化线性表完成!" << endl; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
(3)顺序表赋值:
/** * @brief 利用数组给线性表赋值 * * @param L 目标线性表 * @param arr 使用的数组 * @param len 数组长度 */ void createSqlList(SqlList* L, ElemType arr[], int len) { for (int i = 0; i < len; i++) { L->data[i] = arr[i]; } L->length = len; cout << "创建线性表完成!" << endl; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
(4)顺序表遍历:
/** * @brief 遍历输出线性表 * * @param L 被遍历的线性表 */ void printSqlList(SqlList* L) { if (!L->length) { cout << "当前线性表为空!" << endl; } else { cout << "遍历输出线性表数据:"; for (int i = 0; i < L->length; i++) { cout << L->data[i] << " "; } cout << endl; } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
(5)顺序表查询(索引查询):
/** * @brief 查找某个位置的元素 * * @param L * @param index 指定的位置 * @return ElemType 返回线性表中的元素 */ int searchByIndex(SqlList* L, int index) { if (index > 0 && index <= L->length) { return L->data[index - 1]; } else { cout << "当前指定的位置不存在!" << endl; return -1; } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
(6)顺序表查询(值查询):
/** * @brief 查找某个元素是否存在,如果存在,直接返回查询到的下标 * * @param L 线性表 * @param value 指定的元素 * @return int 如果存在返回线性表中的索引,否则返回-1 */ int isExist(SqlList* L, ElemType value) { int flag = -1; for (int i = 0; i < L->length; i++) { if (L->data[i] == value) { cout << "该线性表中存在目标元素" << value << ",对应的索引为:" << (i) << endl; flag = i; break; } } return flag; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
(7)顺序表删除指定值(全部删除):
/** * @brief 删除线性表中左右的指定元素 * * @param L 线性表 * @param value 指定的被删除的元素 */ void deleteByValue(SqlList* L, ElemType value) { int j = 0; for (int i = 0; i < L->length; i++) { if (L->data[i] != value) { L->data[j++] = L->data[i]; } } L->length = j; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
(8)顺序表指定位置插入指定值:
void insertSqlList(SqlList* L, ElemType value, int index) { if (L->length > MaxSize) { cout << "该线性表已满!" << endl; } else if (index < 0 || index > L->length) { cout << "指定位置不合法!" << endl; } else { int i = L->length - 1; ElemType temp; while (i >= index - 1) { L->data[i + 1] = L->data[i]; i--; } L->data[index - 1] = value; L->length++; } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
无论你使用的哪门语言,肯定会遇到数组,所以上面的顺序表应该是比较熟悉的,所以上面的这些函数应该比较容易理解,稍微注意一下里面的
删除和插入涉及到的元素移动就行。对于时间和空间复杂度,好说,这里就不详细介绍了。下面贴一些完整的代码,方便运行,当然最好还是自己动手写一遍,熟能生巧嘛:#include <iostream> using namespace std; #define MaxSize 50 typedef int ElemType; typedef struct { ElemType data[MaxSize]; int length; } SqlList; /** * @brief 初始化线性表 * * @param L 线性表 */ void initSqlList(SqlList* L) { L->length = 0; cout << "初始化线性表完成!" << endl; } /** * @brief 利用数组给线性表赋值 * * @param L 目标线性表 * @param arr 使用的数组 * @param len 数组长度 */ void createSqlList(SqlList* L, ElemType arr[], int len) { for (int i = 0; i < len; i++) { L->data[i] = arr[i]; } L->length = len; cout << "创建线性表完成!" << endl; } /** * @brief 遍历输出线性表 * * @param L 被遍历的线性表 */ void printSqlList(SqlList* L) { if (!L->length) { cout << "当前线性表为空!" << endl; } else { cout << "遍历输出线性表数据:"; for (int i = 0; i < L->length; i++) { cout << L->data[i] << " "; } cout << endl; } } /** * @brief 查找某个位置的元素 * * @param L * @param index 指定的位置 * @return ElemType 返回线性表中的元素 */ int searchByIndex(SqlList* L, int index) { if (index > 0 && index <= L->length) { return L->data[index - 1]; } else { cout << "当前指定的位置不存在!" << endl; return -1; } } /** * @brief 查找某个元素是否存在,如果存在,直接返回查询到的下标 * * @param L 线性表 * @param value 指定的元素 * @return int 如果存在返回线性表中的索引,否则返回-1 */ int isExist(SqlList* L, ElemType value) { int flag = -1; for (int i = 0; i < L->length; i++) { if (L->data[i] == value) { cout << "该线性表中存在目标元素" << value << ",对应的索引为:" << (i) << endl; flag = i; break; } } return flag; } /** * @brief 删除线性表中左右的指定元素 * * @param L 线性表 * @param value 指定的被删除的元素 */ void deleteByValue(SqlList* L, ElemType value) { int j = 0; for (int i = 0; i < L->length; i++) { if (L->data[i] != value) { L->data[j++] = L->data[i]; } } L->length = j; } /** * @brief 在指定位置插入数据 * * @param L 线性表 * @param value 需要被插入的数据 * @param index 被指定的位置(逻辑位置) */ void insertSqlList(SqlList* L, ElemType value, int index) { if (L->length > MaxSize) { cout << "该线性表已满!" << endl; } else if (index < 0 || index > L->length) { cout << "指定位置不合法!" << endl; } else { int i = L->length - 1; ElemType temp; while (i >= index - 1) { L->data[i + 1] = L->data[i]; i--; } L->data[index - 1] = value; L->length++; } } int main() { SqlList* L = (SqlList*)malloc(sizeof(SqlList)); initSqlList(L); ElemType arr[10] = {1, 2, 3, 3, 5, 3, 7, 8, 9, 10}; createSqlList(L, arr, 10); printSqlList(L); isExist(L, 5); searchByIndex(L, 8); deleteByValue(L, 3); printSqlList(L); insertSqlList(L, 999, 3); printSqlList(L); return 0; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
4.链表的基本操作
三年了,链表这玩意儿我还是学的稀烂,今天再来看看。主要原因:链表不是很好理解,在实际使用的时候大多是被数组代替了,能够先从链表入手“实际问题”的都是大佬。讲个鬼故事:4行代码看两小时还是一脸懵逼,这就是我理解的链表😅😅。
首先来说一些为什么需要使用链表,链表究竟有什么好的,Java直接删掉了指针和引用,但是崛起的GO依然保留了指针?指针,能够指向某段任意大小的内存空间。相比之下,数组需要首先占用一整块固定空间,对于内存扩充不是很方便,容易产生内存碎片。在表示非线性结构时不是很方便,特别是多对多关系,指针在与图有关的问题上有些不可替代的优势。好,咱多的也不多说了,毕竟自己基础也不是很好。
在写代码的时候遇到了一个疑惑:#include <iostream> using namespace std; typedef int ElemType; typedef struct LNode { ElemType data; struct LNode* next; } LNode, *LinkList; /** * @brief 头插法 * * @param L1 被赋值的链表 * @param arr 用来赋值的数组 * @param len 用于赋值的数组的长度 */ void List_HeadInsert(LinkList L, ElemType arr[], int len) { LNode* s; for (int i = 0; i < len; i++) { s = (LinkList)malloc(sizeof(LNode)); s->data = arr[i]; s->next = L->next; L->next = s; } } void displayList(LinkList L) { LNode* p = L->next; cout << "输出链表中的元素:"; while (p != NULL) { cout << p->data << " "; p = p->next; } cout << endl; } int main() { LinkList L = (LinkList)malloc(sizeof(LNode)); L->next = NULL; ElemType arr[5] = {2, 4, 5, 1, 3}; List_HeadInsert(L, arr, 5); displayList(L); return 0; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
这个代码里面没有使用引用类型的参数,但是实际上得到了如下的正确结果:

按照课本和数据结构(李春葆)的书,里面有很多引用或者指针,但是这里既没有使用引用也没有使用指针,同样达到了赋值的目的,难道这种方法更香?大一时候指针对于两个变量的交换属实在自己的脑海里面留下了极深的影响,通过调用函数直接改变了外层的数据(由于理解不够深入,误认为函数直接传递地址,即以地址作为形参,改变能够直接传到外层去):void change_ab(int *a, int *b) { int temp = 0; temp = *a; *a = *b; *b = temp; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
因此看到这里,我顿时觉得无论是王道里面利用回传LinkList还是李春葆的教材都显得有些麻烦,
本着彻底搞懂* &以及这里似显麻烦的目的,于是和好兄弟讨论了半天,最终查到了一个大佬的解释,结合大佬的提示给出如下解释:

发现上面的两个程序的唯一不同就是在update_1函数里面的为形参重新分配了一次空间。前面提到了实参向形参传递参数的时候,会创建一个临时变量(这个变量其实在堆区创建的,便于回收内存),当实参->形参传值的时候,如果传的是数据值,那么形参的函数中会直接创建临时变量,但是如果传递的是地址就不一样了,传递地址,对应的变量需要具有实际意义,因此对应的变量指向与相同的地址,也就是如果不重新分配那么操作的就是同一块地址空间,修改肯定可以传递到外面,这个就解释了为什么我们上面并没有使用引用也没有回传数据能够修改。也就是得到了一个“有点荒谬的结论”:“不给指针形参重新指定空间,那么其功能等价于引用”。如果这个成立,那我俩岂不贼牛逼😏😏。
之后,好兄弟找到了一个学霸,结合学霸的分析得到:之所以不使用引用也能够初始化是因为当实参->形参传值的时候,传递的是地址,被调用的函数里面依然会创建一个临时的指针类型变量,这个变量指向的内存地址也就是传入的内存地址,这个变量实际对这块内存指向的值的修改会被传递到外面去。因为站在指针的角度上来说,指针只关注于内存地址的指向,不关注内部的值,通过另外一个指针指向这个内存地址并修改,之后使用其他指向这个内存地址访问,得到的肯定是修改过的数据,也就解释了指针交换和这里的链表赋值。回到那个update_1函数里面,因为在函数里面中途修改了临时变量的指向,所以也就是直接与外部无关了
接下来,回到理解荒谬的结论上来,确实效果可以等价这么理解,但是最好还是不要这么说,如果想要修改传递出去使用引用类型还是更加直观,其实也就是多加了&符号。另外再来解释一下你可能像我一样质疑两次displayList(L)在等效引用下为什么结果还是一致的,其实因为这里还创建了一个p的工作指针,对于遍历其实是通过p来实现的,也就是上面说的又加了一个指向与这块内存空间的指针,用这个指针扫描了一次这个内存地址里面的值,这个显然是不更改具体内容的,难不成看一下还得嫁给他😀😀。终于理解通顺了!!!🌟🌟🌟
最后通过查阅大佬的论坛发言得到如下的结论:
(1)给一个函数传值,实参会把具体的值传给函数的形参,函数拿到这个值以后会产生一个临时变量(这个临时变量是不可见的),整个函数的操作就是在操作这个临时变量,所以你在函数内部给,形参赋值并不能改变实参的值。
(2)给一个函数传指针,实参会把外部存储值的地址给形参,注意这是地址,证明外部已经申明了存储该实参值的内存,不然不会存在存储某值的地址,所以内部不再需要分配空间;若不重新指向新的内存空间,操作是同一块地址;
(3)当然有的时候我们的实参只申明了一个指针,并没有申请地址,这个时候编译是没有问题的,但是在运行的时候我们会把实参指向的内容的地址传给形参,而此时实参并没有申请空间,这个时候就会出现一个错误。当我们传递给函数一个指针的时候,我们的目的是要操作某一块内存,既然要操作某一块内存,那么这块内存首先必须存在,既然已经存在在函数内部在分配空间就没有必要,即使分配了也没有任何意义(比如这里第一个程序里面的update_1函数),如果不释放还会出现内存泄露情况。给个错误的例子吧:
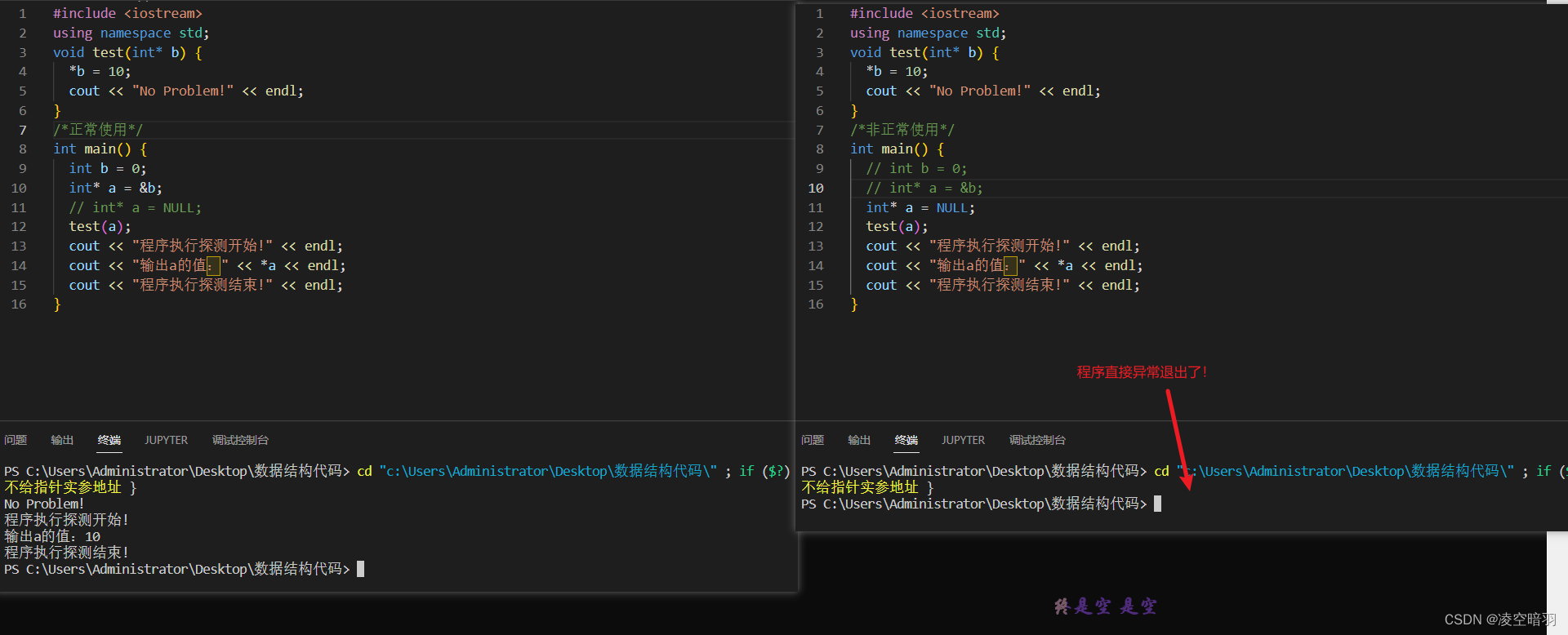
为了更好的说明问题,这里使用Viusal Studio再来杠一下,这个软件对于C++更加专业(本质是因为Windows SDK):
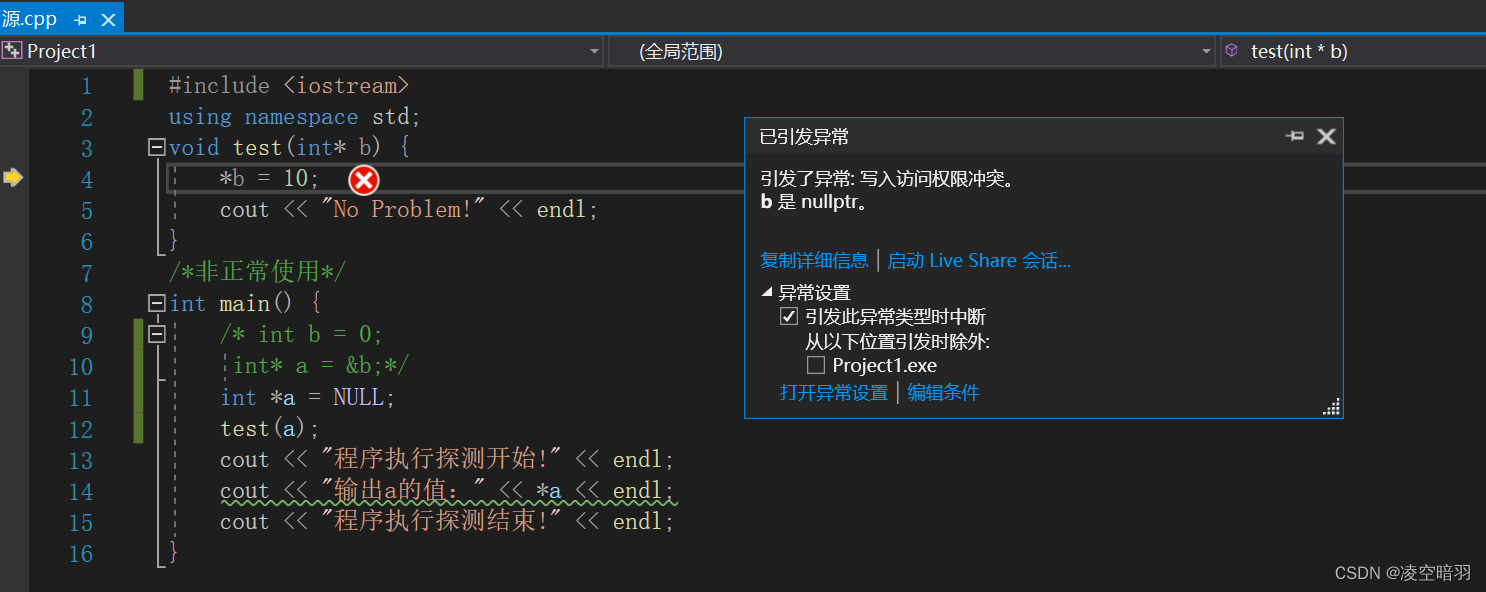
最后结合Visual Studio的优化建议对程序优化(请求并不是每一次都能够成功请求到内存块):/** * @brief 头插法 * * @param L1 被赋值的链表 * @param arr 用来赋值的数组 * @param len 用于赋值的数组的长度 */ void List_HeadInsert(LinkList L, ElemType arr[], int len) { for (int i = 0; i < len; i++) { LNode* s = (LinkList)malloc(sizeof(LNode)); if (s) { s->data = arr[i]; s->next = L->next; L->next = s; } } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
说明:由于王道提供的教材并没有想
VS Studio分析这个内存能否申请成功,默认也是能够申请,因为我们申请的内存通常比较小,现在的计算机内存比较大,在申请大内存或者数据量比较答的时候再做判断即可,对于考研不用纠结这个。因此后面的算法为了更好的聚焦核心实现代码,就不写这些内存请求是否成功的判断了。
因此在使用数据操作的时候,如果需要将修改传入外层,可以直接使用&这样也方便理解一些。但还是需要理解不加&也能达到修改目的的原理。
回到链表的基本操作上来:
(1)链表结构:typedef int ElemType; typedef struct LNode { ElemType data; struct LNode* next; } LNode, *LinkList;- 1
- 2
- 3
- 4
- 5
(2)头插法:
/** * @brief 头插法 * * @param L1 被赋值的链表 * @param arr 用来赋值的数组 * @param len 用于赋值的数组的长度 */ void List_HeadInsert(LinkList& L, ElemType arr[], int len) { LNode* s; for (int i = 0; i < len; i++) { s = (LinkList)malloc(sizeof(LNode)); s->data = arr[i]; s->next = L->next; L->next = s; } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
(2)尾插法
/** * @brief 尾插法,这里的p指针又被称为工作指针,如果 * 不适用p指针,由于尾插法最后需要L->next=NULL,尬住了 * 可以把s理解成珠子,L为串珠子的头,p来把珠子串起来 * * @param L 引用类型的指针,目的是将修改传递出去 * @param arr 包含数据的数组 * @param len 数组长度 */ void List_TailInsert(LinkList& L, ElemType arr[], int len) { LNode *s, *p = L; for (int i = 0; i < len; i++) { s = (LinkList)malloc(sizeof(LNode)); s->data = arr[i]; p->next = s; p = s; } p->next = NULL; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
(3)链表插入(根据逻辑位置):
/** * @brief 通过逻辑顺序添加指定元素,关键就在于查找逻辑位置的上一个元素,如果 * 逻辑位置小于1插入最前面,如果逻辑位置大于线性表总元素数量,插入到最后面 * * @param L 引用类型地址,方便将改变传到函数外部 * @param value 需要插入的值 * @param index 逻辑地址索引 */ void List_InsertByIndex(LinkList& L, ElemType value, int index) { int i = 0; LNode* p = L; while (i < index - 1 && p->next != NULL) { p = p->next; i++; } LNode* s = (LNode*)malloc(sizeof(LNode)); s->data = value; s->next = p->next; p->next = s; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
(4)根据逻辑位置查询节点
/** * @brief 依据索引查找元素 * * @param L 被查找的链表 * @param index 逻辑位置 * @param target 存储目标几点的引用 */ void searchByIndex(LinkList L, int index, LNode*& target) { int i = 0; LNode* p = L->next; if (index < 1) { cout << "逻辑位置不合法!" << endl; target = NULL; } while (i < index - 1 && p != NULL) { i++; p = p->next; } target = p; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
(5)根据值,查询在线性表中第一次出现的位置:
/** * @brief 依据索引查找元素,为0表示未查询到节点 * * @param L 被查找的链表 * @param value 需要匹配的值 * @param target 存储目标几点的引用 */ void searchByValue(LinkList L, ElemType value, int& target) { LNode* p = L->next; int i = 1; target = 0; while (p != NULL) { if (p->data == value) { target = i; break; } p = p->next; i++; } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
(6)根据逻辑位置删除节点:
/** * @brief * 按照逻辑位置删除指定节点,如果逻辑位置大于最后一个节点直接删除尾结点,删除节点的时候需要 * 注意:不能使用p-next=p->next->next;free(p)这样会导致线性表断开,需要使用额外的指针辅助。 * * @param L 引用类型参数将修改传出 * @param index 逻辑位置 */ void deleteByIndex(LinkList& L, int index) { int i = 1; LNode* p = L->next; if (index < 1) { cout << "当前的逻辑位置不合法!" << endl; return; } while (i < index && p->next != NULL) { p = p->next; i++; } LNode* q = p->next; p->next = q->next; free(q); }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
(7)根据指定值删除节点
/** * @brief 根据指定值删除全部的节点 * * @param L 引用类型参数,将修改传递到外部 * @param value 针对的值 */ void deleteByValue(LinkList& L, ElemType value) { LNode *pre = L, *p = L->next, *temp; while (p != NULL) { if (p->data == value) { temp = p; p = p->next; pre->next = p; free(temp); } else { pre = p; p = p->next; } } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
(8)链表遍历
/** * @brief 根据数值删除元素,需要删除全部匹配的元素 * * @param L 引用型参数,改变能够传递到函数外面去 */ void displayList(LinkList L) { cout << "输出链表中的元素:"; LNode* p = L->next; while (p != NULL) { cout << p->data << " "; p = p->next; } cout << endl; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
(9)链表销毁:
/** * @brief 链表的销毁,从头结点依次向后销毁,在销毁链表的时候 * 其实就没有头结点这个概念了,每个节点等价,最后需要防止野指针 * * @param L */ void ListDestory(LinkList& L) { LNode *p = L, *q; while (p != NULL) { q = p->next; free(p); p = q; } L = NULL; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
最后为了方便大家调试全部贴一次代码:
#include <iostream> using namespace std; typedef int ElemType; typedef struct LNode { ElemType data; struct LNode* next; } LNode, *LinkList; /** * @brief 头插法 * * @param L1 被赋值的链表 * @param arr 用来赋值的数组 * @param len 用于赋值的数组的长度 */ void List_HeadInsert(LinkList& L, ElemType arr[], int len) { LNode* s; for (int i = 0; i < len; i++) { s = (LinkList)malloc(sizeof(LNode)); s->data = arr[i]; s->next = L->next; L->next = s; } } /** * @brief 尾插法,这里的p指针又被称为工作指针,如果 * 不适用p指针,由于尾插法最后需要L->next=NULL,尬住了 * 可以把s理解成珠子,L为串珠子的头,p来把珠子串起来 * * @param L 引用类型的指针,目的是将修改传递出去 * @param arr 包含数据的数组 * @param len 数组长度 */ void List_TailInsert(LinkList& L, ElemType arr[], int len) { LNode *s, *p = L; for (int i = 0; i < len; i++) { s = (LinkList)malloc(sizeof(LNode)); s->data = arr[i]; p->next = s; p = s; } p->next = NULL; } /** * @brief 通过逻辑顺序添加指定元素,关键就在于查找逻辑位置的上一个元素,如果 * 逻辑位置小于1插入最前面,如果逻辑位置大于线性表总元素数量,插入到最后面 * * @param L 引用类型地址,方便将改变传到函数外部 * @param value 需要插入的值 * @param index 逻辑地址索引 */ void List_InsertByIndex(LinkList& L, ElemType value, int index) { int i = 0; LNode* p = L; while (i < index - 1 && p->next != NULL) { p = p->next; i++; } LNode* s = (LNode*)malloc(sizeof(LNode)); s->data = value; s->next = p->next; p->next = s; } /** * @brief 依据索引查找元素 * * @param L 被查找的链表 * @param index 逻辑位置 * @param target 存储目标几点的引用 */ void searchByIndex(LinkList L, int index, LNode*& target) { int i = 0; LNode* p = L->next; if (index < 1) { cout << "逻辑位置不合法!" << endl; target = NULL; } while (i < index - 1 && p != NULL) { i++; p = p->next; } target = p; } /** * @brief 依据索引查找元素 * * @param L 被查找的链表 * @param value 需要匹配的值 * @param target 存储目标几点的引用 */ void searchByValue(LinkList L, ElemType value, int& target) { LNode* p = L->next; int i = 1; target = 0; while (p != NULL) { if (p->data == value) { target = i; break; } p = p->next; i++; } } /** * @brief * 按照逻辑位置删除指定节点,如果逻辑位置大于最后一个节点直接删除尾结点,删除节点的时候需要 * 注意:不能使用p-next=p->next->next;free(p)这样会导致线性表断开,需要使用额外的指针辅助。 * * @param L 引用类型参数将修改传出 * @param index 逻辑位置 */ void deleteByIndex(LinkList& L, int index) { int i = 1; LNode* p = L->next; if (index < 1) { cout << "当前的逻辑位置不合法!" << endl; return; } while (i < index && p->next != NULL) { p = p->next; i++; } LNode* q = p->next; p->next = q->next; free(q); } /** * @brief 根据指定值删除全部的节点 * * @param L 引用类型参数,将修改传递到外部 * @param value 针对的值 */ void deleteByValue(LinkList& L, ElemType value) { LNode *pre = L, *p = L->next, *temp; while (p != NULL) { if (p->data == value) { temp = p; p = p->next; pre->next = p; free(temp); } else { pre = p; p = p->next; } } } /** * @brief 根据数值删除元素,需要删除全部匹配的元素 * * @param L 引用型参数,改变能够传递到函数外面去 */ void displayList(LinkList L) { cout << "输出链表中的元素:"; LNode* p = L->next; while (p != NULL) { cout << p->data << " "; p = p->next; } cout << endl; } /** * @brief 链表的销毁,从头结点依次向后销毁,在销毁链表的时候 * 其实就没有头结点这个概念了,每个节点等价,最后需要防止野指针 * * @param L */ void ListDestory(LinkList& L) { LNode *p = L, *q; while (p != NULL) { q = p->next; free(p); p = q; } L = NULL; } int main() { LinkList L = (LinkList)malloc(sizeof(LNode)); L->next = NULL; LNode* target; int position; ElemType arr[6] = {2, 4, 5, 1, 3, 3}; List_HeadInsert(L, arr, 6); displayList(L); ListDestory(L); L = (LinkList)malloc(sizeof(LNode)); L->next = NULL; List_TailInsert(L, arr, 6); displayList(L); List_InsertByIndex(L, 999, 91); displayList(L); searchByIndex(L, 5, target); if (target) { cout << "输出按照逻辑位置查找的指定值为:" << target->data << endl; } searchByValue(L, 999, position); if (position) { cout << "输出按照值查找,第一次出现999的是第" << position << "个" << endl; } deleteByIndex(L, 1); displayList(L); deleteByValue(L, 3); displayList(L); ListDestory(L); return 0; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
- 173
- 174
- 175
- 176
- 177
- 178
- 179
- 180
- 181
- 182
- 183
- 184
- 185
- 186
- 187
- 188
- 189
- 190
- 191
- 192
- 193
- 194
- 195
- 196
- 197
- 198
- 199
- 200
- 201
- 202
- 203
- 204
5.为什么要手动销毁申请的内存?
回到理论上来,还及得大一的时候老师十分强调手动销毁申请的空间,防止出现内存泄露。我当时就慌了,作为萌新,编码写的贼捞,那要是我一不小心忘了岂不尬住了,更何况我电脑本身才8G,辅存也才200G。那要是我写个循环,调调bug岂不尬住了,等下自己把电脑整崩溃了。实不相瞒,当时甚至晚上做梦,写着写着电脑炸了😏😏。借鉴大佬的解释:
(1)平时写的代码关闭之后,即使存在内存泄露也会被操作系统回收,在Java语言中就提到内存回收机制,可见这种回收机制是可以真实存在的;
(2)那为什么还得自己释放呢?有些操作系统不能够自己回收这些被泄露的内存,这样确实存在产生内存碎片的可能;不是所有程序都像我们写的程序跑一下就关闭了,还有大多数程序是服务端的守护进程,是一直运行的,如果存在内存泄漏,那么经过长时间的累计,会造成严重问题,程序会崩溃,操作系统的性能和稳定性也会受到很大影响。6.线性表的其他知识
6.1双链表
双链表,双链表和单链表十分相似,能够很方便的查找和操作一个节点的前驱和后继,比如双向链表能够根据节点同时向两边查询。这里就写简单些:
(1)结构如下:typedef int ElemType; typedef struct LNode { struct LNode* prior; ElemType data; struct LNode* next; } LNode, *LinkList;- 1
- 2
- 3
- 4
- 5
- 6
(2)部分经典用法如下:
#include <iostream> using namespace std; typedef int ElemType; typedef struct LNode { struct LNode* prior; ElemType data; struct LNode* next; } LNode, *LinkList; /** * @brief 头插法构建双向链表 * * @param L 使用引用类型,将改变传递到函数外面 * @param arr 用于赋值的数组 * @param len 数组的长度 */ void List_HeadInsert(LinkList& L, ElemType arr[], int len) { LNode* s; for (int i = 0; i < len; i++) { s = (LNode*)malloc(sizeof(LNode)); s->data = arr[i]; s->next = L->next; s->prior = L; L->next = s; } } /** * @brief 利用尾插法为双向链表赋值,需要使用额外的变量,和单链表一样, * 如果不适用额外的指针变量(工作指针),最后必出现L->next=NULL,尬住了 * * @param L 引用类型参数,将数据传递到函数外部 * @param arr 用来给双向链表赋值的数组 * @param len 数组的长度 */ void List_TailInsert(LinkList& L, ElemType arr[], int len) { LNode *s, *p = L; for (int i = 0; i < len; i++) { s = (LNode*)malloc(sizeof(LNode)); s->data = arr[i]; p->next = s; s->prior = p; p = s; } s->next = NULL; } /** * @brief 指定逻辑位置插入指定数据 * * @param L 引用类型的指针变量,使得改变能够传递到函数外面 * @param value 需要插入的值 * @param index 插入值得逻辑位置 */ void List_InsertByIndex(LinkList& L, ElemType value, int index) { int i = 1; LNode* p = L; if (index < 1) { cout << "当前逻辑位置不合法!" << endl; } else { while (i < index && p->next != NULL) { i++; p = p->next; } LNode* s = (LNode*)malloc(sizeof(LNode)); s->data = value; s->next = p->next; s->prior = p; p->next = s; } } /** * @brief 根据值删除线性表中所有给定的值,注意使用临时 * 变量标记需要被删除的对象能够使代码和思路更加清晰 * * @param L 引用类型参数,方便将改变传递出去 * @param value 指定需要删除的值 */ void List_DeleteByValue(LinkList& L, ElemType value) { LNode *p = L->next, *q = L, *temp; while (p != NULL) { if (p->data == value) { temp = p; p = p->next; q->next = p; p->prior = q; free(temp); } else { q = p; p = p->next; } } } /** * @brief 遍历的线性表 * * @param L 不使用引用,防止修改 */ void displayList(LinkList L) { LNode* p = L->next; cout << "输出双链表中的数据:"; while (p != NULL) { cout << " " << p->data; p = p->next; } cout << endl; } /** * @brief 销毁双向链表,其实和单向链表一致,只是还可以向前销毁 * * @param L 需要被销毁的对象,需要使用引用类型,需要最后防止野指针 */ void ListDestroy(LinkList& L) { LNode *p = L, *q; while (p != NULL) { q = p; p = p->next; free(q); } L = NULL; } int main() { LNode* L = (LinkList)malloc(sizeof(LNode)); L->prior = NULL; L->next = NULL; ElemType arr[5] = {3, 4, 4, 1, 5}; List_TailInsert(L, arr, 5); displayList(L); List_InsertByIndex(L, 999, 4); displayList(L); List_DeleteByValue(L, 4); displayList(L); ListDestroy(L); return 0; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
6.2静态链表
所谓的静态链表其实借用数组来线性描述线性表的链式存储结构,基本结构如下:
#define MaxSize 50 typedef int ElemType; typedef struct LNode { ElemType data; int next; } SLinkList[MaxSize];- 1
- 2
- 3
- 4
- 5
- 6
需要明确,静态链表以
next=-1作为链表结束的标志,对于静态链表的插入和删除和动态链表类似,只需要修改里面的下标,是链式结构和顺序结构的一种中和,举例如下:

6.3链表逆序
链表逆序算是一个理解难度系数比较高的问题,首先如果是只需要逆序输出,那么可以直接利用递归实现:
#include <iostream> using namespace std; typedef int ElemType; typedef struct LNode { ElemType data; LNode* next; } LNode, *LinkList; /** * @brief 头插法 * * @param L1 被赋值的链表 * @param arr 用来赋值的数组 * @param len 用于赋值的数组的长度 */ void List_HeadInsert(LinkList& L, ElemType arr[], int len) { LNode* s; for (int i = 0; i < len; i++) { s = (LinkList)malloc(sizeof(LNode)); s->data = arr[i]; s->next = L->next; L->next = s; } } /** * @brief 根据数值删除元素,需要删除全部匹配的元素 * * @param L 引用型参数,改变能够传递到函数外面去 */ void displayList(LinkList L) { cout << "输出链表中的元素:"; LNode* p = L->next; while (p != NULL) { cout << p->data << " "; p = p->next; } cout << endl; } /** * @brief 逆序输出线性表中间的数据 * * @param L 非引用类型参数 */ void ReverseDisplay(LinkList L) { if (L->next != NULL) { ReverseDisplay(L->next); } if (L != NULL) { cout << L->data << " "; } } int main() { LinkList L = (LinkList)malloc(sizeof(LNode)); L->next = NULL; LNode* target; int position; ElemType arr[6] = {2, 4, 5, 1, 3, 3}; List_HeadInsert(L, arr, 6); displayList(L); cout << "逆序输出单链表数据:"; ReverseDisplay(L->next); return 0; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
如果是需要真实的将链表逆序,那么可以联想一下头插法,利用头插法将数组里面的数据赋值给线性表得到的刚好是逆序的。得到的思路如下:

结合上面的分析可以得到如下代码:#include <iostream> using namespace std; typedef int ElemType; typedef struct LNode { ElemType data; LNode* next; } LNode, *LinkList; /** * @brief 头插法 * * @param L1 被赋值的链表 * @param arr 用来赋值的数组 * @param len 用于赋值的数组的长度 */ void List_HeadInsert(LinkList& L, ElemType arr[], int len) { LNode* s; for (int i = 0; i < len; i++) { s = (LinkList)malloc(sizeof(LNode)); s->data = arr[i]; s->next = L->next; L->next = s; } } /** * @brief 根据数值删除元素,需要删除全部匹配的元素 * * @param L 引用型参数,改变能够传递到函数外面去 */ void displayList(LinkList L) { cout << "输出链表中的元素:"; LNode* p = L->next; while (p != NULL) { cout << p->data << " "; p = p->next; } cout << endl; } /** * @brief 利用头插法的思想实现链表的逆置,对代码附加说明,使用p指针和r指针, * p指针为工作指针,r指针用于记录p指针的下一个指针,防止线性表断开。首先是 * 处理空头,然后将后面的节点依次插入首节点的前面,在循环体中:首先记录工作 * 节点的下一个节点,保证不会丢失对链的追踪,循环体里面的第二三句好理解,就是 * 左边插入,第四句就是回到追踪路径上,依次处理余下的节点。最后分析尾结点也 * 就是关注最后逆置的链表的头的问题,发现这里最后执行的是L->next指向最后一个 * 被提前的节点,刚好说明这个头没有问题,即两边完成了。最后补充说明,空头还是 * 头结点,也就是不会出现访问没有初始化的data的情况。 * * @param L 引用类型参数,方便将修改传递到函数外部去 */ void List_Reverse(LinkList& L) { LNode *p = L->next, *r; L->next = NULL; while (p != NULL) { r = p->next; p->next = L->next; L->next = p; p = r; } } int main() { LinkList L = (LinkList)malloc(sizeof(LNode)); L->next = NULL; LNode* target; int position; ElemType arr[6] = {2, 4, 5, 1, 3, 3}; List_HeadInsert(L, arr, 6); displayList(L); List_Reverse(L); cout << "逆序输出单链表数据:"; displayList(L); return 0; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
如果你能看到这里,真的很感谢你💓!当然很陈恳的说,并不是看完或者理解一次就会了,需要反复理解甚至是使用才能更灵活的掌握线性表。等哪天你遇到“实际问题”,你能首先想着使用链表来解决问题,那个时候你才能说是掌握的比较好了!😀😀😀
plus:文章并没有介绍实际引用题,比如比较经典的利用指针合并两个数列,链表的排序(其实链表排序可以使用空间换时间的思维,利用顺序表里面O(nlog2n)算法处理然后回存链表)等,感兴趣的话可以去找找大佬们的文章哦,再次感谢💓💓! -
相关阅读:
Spring AOP的失效场景
SAP 采购订单抬头屏幕增强(SMOD)
字节面试:如何解决MQ消息积压问题?
竞赛 深度学习YOLO安检管制物品识别与检测 - python opencv
java计算机毕业设计任务进度监督的软件项目实训管理系统源码+数据库+系统+lw文档+mybatis+运行部署
Unity编辑器扩展: 程序化打图集工具
pytest运行时参数说明,pytest详解,pytest.ini详解
ClickHouse相关SQL总结:创建表、分区主键排序设置、删除表、删除分区、修改表字段
Linux ubuntun 手动安装配置OpenJDK1.8
13_星仔带你学Java之接口、内部类、枚举
- 原文地址:https://blog.csdn.net/weixin_46560512/article/details/125456965
