-
MCS:离散随机变量——Hyper Geometric分布
Hyper Geometric
超几何分布是统计学上一种离散概率分布。它描述了从有限N个物件(其中包含D个指定种类的物件)中(不放回)抽出n个物件,成功抽出该指定种类的物件的数量记为 x x x,变量 x x x称为超几何分布, x ∼ H ( N , n , D ) x \sim H(N, n, D) x∼H(N,n,D)。 x x x的取值范围为: 0 ∼ M i n ( D , n ) 0 \sim Min(D,n) 0∼Min(D,n)之间的整数。
P ( x ) = C D x C N − D n − x C N n , x = 0 ∼ M i n ( n , D ) P(x) = \frac{C_D^x C_{N - D}^{n - x}}{C_N^n},x = 0 \sim Min(n, D) P(x)=CNnCDxCN−Dn−x,x=0∼Min(n,D)
期望和方差:
E ( x ) = n D N E(x) = \frac{nD}{N} E(x)=NnD
V ( x ) = n × D N × ( 1 − D N ) × N − n N − 1 V(x) = n \times \frac{D}{N} \times ( 1 - \frac{D}{N}) \times \frac{N- n}{N - 1} V(x)=n×ND×(1−ND)×N−1N−n
生成超几何分布变量
- 样本总量为: N N N, 特定种类样本数量为: D D D, 不放回抽样次数: n n n, x = 0 x = 0 x=0
- For
i
=
1
→
n
i = 1 \to n
i=1→n:
- p = D N p = \frac{D}{N} p=ND
- Generate u , u ∼ U ( 0 , 1 ) u,u \sim U(0, 1) u,u∼U(0,1)
- N = N − 1 N = N - 1 N=N−1
- if u < p , x = x + 1 , D = D − 1 u < p, x = x + 1,D = D - 1 u<p,x=x+1,D=D−1
- Next i i i
- Return x x x
例:假设一共有10个样本,其中有两个存在缺陷,从中不放回抽出4个样本,在抽样的样本中观察到存在缺陷的样本数量是一个随机的超几何变量。
- N = 10 , D = 2 , n = 4 , x = 0 N = 10,D = 2,n = 4, x = 0 N=10,D=2,n=4,x=0
- i = 1 , P = 2 / 10 = 0.2 , u = 0.37 , u > P , N = N − 1 = 9 i = 1,P = 2/10 = 0.2,u = 0.37,u > P, N = N - 1 = 9 i=1,P=2/10=0.2,u=0.37,u>P,N=N−1=9
- i = 2 , P = 2 / 9 = 0.222 , u = 0.51 , u > P , N = N − 1 = 8 i = 2,P = 2/9 = 0.222,u = 0.51,u > P, N = N - 1 = 8 i=2,P=2/9=0.222,u=0.51,u>P,N=N−1=8
- i = 3 , P = 2 / 8 = 0.25 , u = 0.14 , u < P , N = N − 1 = 7 , D = D − 1 = 1 , x = x + 1 i = 3,P = 2/8 = 0.25,u = 0.14,u < P,N = N - 1 = 7,D = D - 1 = 1,x = x + 1 i=3,P=2/8=0.25,u=0.14,u<P,N=N−1=7,D=D−1=1,x=x+1
- i = 4 , P = 1 / 7 = 0.143 , u = 0.84 , u > P , N = N − 1 = 6 i = 4,P = 1/7 = 0.143,u = 0.84,u > P,N = N - 1 = 6 i=4,P=1/7=0.143,u=0.84,u>P,N=N−1=6
- x = 1 x = 1 x=1
模拟生成超几何变量
import numpy as np import matplotlib.pyplot as plt- 1
- 2
def generate_hyper_geometric(N=100, D=10, n=10): x = 0 for i in range(n): p = D/N u = np.random.uniform(0, 1) N -= 1 if u < p: x += 1 D -= 1 return x- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
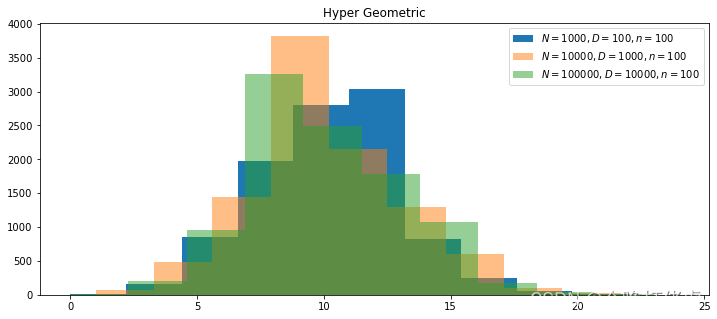
-
相关阅读:
GBase 8c 技术白皮书 三
协程简单使用
学习如何编码
[需求管理-8]:需求分析 - 商业价值评判和确认
部署Kubernetes Dashboard
ITextRenderer将PDF转换为HTML详细教程
SPI通信协议
Android12.0首次开机默认授予app运行时权限(去掉运行时授权弹窗)第二种方法
静态变 量
面向对象编程第二式:继承 (Java篇)
- 原文地址:https://blog.csdn.net/u014281392/article/details/125474696