-
矩阵分析与应用+张贤达
第一章 矩阵与线性方程组(十一)
1.向量的内积与范数
根据元素取值方式的不同,向量分为常数向量、函数向量和随机向量。
- 常数向量是元素为常数的向量
- 函数向量是元素取某个变量的函数值的向量
- 随机向量是元素为随机变量的向量。
虽然常数向量、函数向量和随机向量的内积定义公式有所不同,但是无论向量取何种形式,向量的内积和范数都必须服从一定的公理。
由于实向量是复向量的特例,下面以复向量作为讨论对象,并用 R R R和 C C C分别代表实数域和复数域。
令 V V V是复向量空间。
函数 < x , y > : V ∗ V → C <x,y>:V*V→C <x,y>:V∗V→C称为向量 x x x与 y y y的内积,若对所有 x , y , z ∈ V x,y,z \in V x,y,z∈V,以下内积公理满足:
(1) < x , x > ≥ 0 <x,x> ≥ 0 <x,x>≥0 (非负性)
(1a) < x , x > = 0 <x,x>=0 <x,x>=0,当且仅当 x = 0 x=0 x=0 (正性)
(2) < x + y , z > = < x , z > + < y , z > <x+y,z>=<x,z>+<y,z> <x+y,z>=<x,z>+<y,z> (可加性)
(3) < c x , y > = c ∗ < x , y > <cx,y>=c*<x,y> <cx,y>=c∗<x,y>,对所有复常数c成立 (齐次性)
(4) < x , y > = < y , x > ∗ <x,y>=<y,x>* <x,y>=<y,x>∗ (Hermitian性)
式中,*表示复数共轭。令V是复向量空间。
函数 ∣ ∣ x ∣ ∣ : V → R ||x||:V→R ∣∣x∣∣:V→R称为向量 x x x的范数,若对所有 x , y ∈ V x,y \in V x,y∈V,下面的范数公理成立:
(1) ∣ ∣ x ∣ ∣ ≥ 0 ||x||≥0 ∣∣x∣∣≥0 (非负性)
(1a) ∣ ∣ x ∣ ∣ = 0 ||x||=0 ∣∣x∣∣=0,当且仅当 x = 0 x=0 x=0 (正性)
(2) ∣ ∣ c x ∣ ∣ = ∣ c ∣ ∣ ∣ x ∣ ∣ ||cx||=|c| ||x|| ∣∣cx∣∣=∣c∣∣∣x∣∣,对所有复常数c成立 (齐次性)
(3) ∣ ∣ x + y ∣ ∣ ≤ ∣ ∣ x ∣ ∣ + ∣ ∣ y ∣ ∣ ||x+y||≤||x||+||y|| ∣∣x+y∣∣≤∣∣x∣∣+∣∣y∣∣ (三角不等式)
上述公理是平面上的Euclidean长度的熟知性质。满足公理(1),(2),(3),但不一定满足公理(1a)的函数称为向量的半范数。2.常数向量的内积与范数
两个 m x I mxI mxI维常数向量 x = [ x 1 , x 2 , … , x m ] T x=[x_1,x_2,…,x_m]^T x=[x1,x2,…,xm]T和 y = [ y 1 , y 2 , … , y m ] T y=[y_1,y_2,…,y_m]^T y=[y1,y2,…,ym]T的内积(或叫点积)定义为
< x , y > = x H y = ∑ i = 1 m x i ∗ y i <x,y>=x^Hy=\sum_{i=1}^mx_i^*y_i <x,y>=xHy=i=1∑mxi∗yi
两个向量之间的夹角定义为
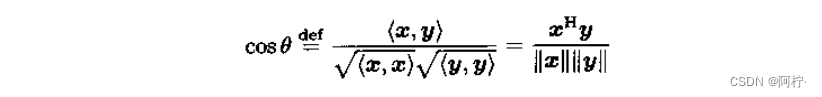
显然,若 x H y = 0 x^Hy=0 xHy=0,则 θ = π / 2 θ=\pi/2 θ=π/2。此时,称常数向量 x x x和 y y y正交。因此,两个常数向量正交的数学定义如下。两个常数向量称为正交,若它们的内积等于零,即 x H y = 0 x^Hy=0 xHy=0,并记作 x ⊥ y x \bot y x⊥y.
根据定义知,零向量 0 0 0与同一空间的任何向量都正交。-
序列 e x p ( j 2 π f m ) {exp(j2πfm)} exp(j2πfm)是一个以单位时间间隔被采样的频率为 f f f的正弦波。复正弦波向量 e m ( f ) e_m(f) em(f)定义为 ( m + 1 ) x 1 (m+1)x1 (m+1)x1向量,即
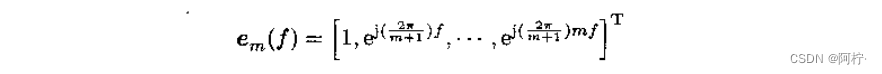
这样一来, N N N个数据样本 x ( n ) , n = 0 , 1 , ⋅ ⋅ ⋅ , N − 1 x(n),n=0,1,···,N-1 x(n),n=0,1,⋅⋅⋅,N−1的离散Fourer变换(DFT)就可以用向量的内积表示为
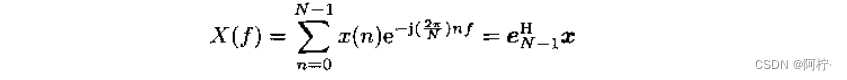
其中, x = [ x ( 0 ) , x ( 1 ) , … , x ( N − 1 ) ] T x=[x(0),x(1),…,x(N-1)]^T x=[x(0),x(1),…,x(N−1)]T常称为数据向量。 -
几种常用的向量范数
(1) l 1 l_1 l1范数
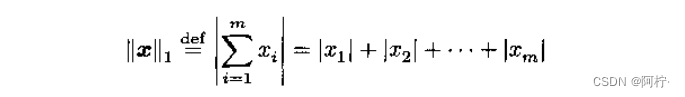
上述范数有时也叫和范数或 1 1 1范数。
(2) l 2 l_2 l2范数
∣ ∣ x ∣ ∣ 2 = ( ∣ x 1 ∣ 2 + ∣ x 2 ∣ 2 + … + ∣ x n ∣ 2 ) 1 / 2 ||x||_2 =(|x_1|^2 +|x_2|^2 +…+|x_n|^2)^{1/2} ∣∣x∣∣2=(∣x1∣2+∣x2∣2+…+∣xn∣2)1/2
这一范数常称Euclidean范数,有时也称Frobenius范数。
(3) l ∞ l_∞ l∞范数
∣ ∣ x ∣ ∣ ∞ = m a x ( ∣ x 1 ∣ , ∣ x 2 ∣ , ⋅ ⋅ ⋅ , ∣ x n ∣ ) ||x||_∞= max(|x_1|,|x_2|,···,|x_n|) ∣∣x∣∣∞=max(∣x1∣,∣x2∣,⋅⋅⋅,∣xn∣)
也称无穷范数或极大范数。
(4) l p l_p lp范数
∣ ∣ x p ∣ ∣ = ( ∑ i = 1 m ∣ x i ∣ p ) 1 / p , p ≥ 1 ||x_p||=(\sum_{i=1}^m|x_i|^p)^{1/p},p≥1 ∣∣xp∣∣=(i=1∑m∣xi∣p)1/p,p≥1
l p l_p lp范数也叫 Hölder 范数
当p=2时, l p l_p lp范数与Euclidean范数完全等价。
另外,无穷范数是 l p l_p lp范数的极限形式,即有
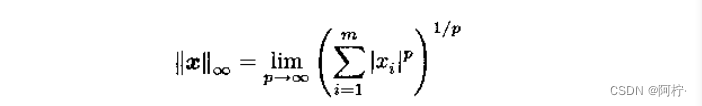
范数||x||称为酉不变的,若 ∣ ∣ U x ∣ ∣ = ∣ ∣ x ∣ ∣ ||Ux||=||x|| ∣∣Ux∣∣=∣∣x∣∣对所有向量 x ∈ C m x \in C^m x∈Cm和所有酉矩阵 U ∈ C m x m U \in C^{mxm} U∈Cmxm恒成立。 -
Euclidean范数 ∣ ∣ ⋅ ∣ ∣ ||·|| ∣∣⋅∣∣是酉不变的。
假定向量 x x x和 y y y有共同的起点(即原点 O O O),它们的端点分别为 x x x和 y y y,则 ∣ ∣ x − y ∣ ∣ 2 ||x-y||_2 ∣∣x−y∣∣2度量两个向量 x , y x,y x,y两端点x,y之间的标准Euclidean距离。
特别地,非负的标量 < x , x > 1 / 2 <x,x>^{1/2} <x,x>1/2称为向量 x x x的Euclidean长度。Euclidean长度为1的向量叫做归一化(或标准化)向量。对于任何不为零的向量 x ∈ C m x\in C^m x∈Cm,向量 x / < x , x > 1 / 2 x/<x,x>^{1/2} x/<x,x>1/2都是归一化的,并且它与 x x x同方向。 -
Euclidean范数是应用最为广泛的向量范数定义。在本书后面的讨论中,如无特别声明,向量范数均指 Euclidean范数。
常数向量 w w w和 v v v的外积(乂叫叉积)记作 w v H wv^H wvH,定义为
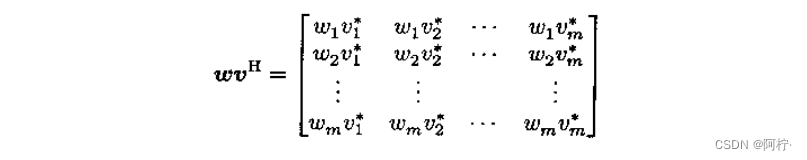
-
相关阅读:
Miracast专业术语
Java- IO流
hive-udf
STL::string简单介绍
微软笔试2022.8.25
12029.EEPROM驱动框架
java第七讲:类中的关键字
anaconda安装pytorch
TDengine 成功“晋级” Percona Live 2023 银牌赞助商,开发者驻足关注
Science子刊新发现:mtDNA损伤或可提前诊断帕金森病
- 原文地址:https://blog.csdn.net/m0_45085885/article/details/125473435