动态规划--背包问题

在学习编程的时候，我们学习的第一个程序基本都是hello world，而背包问题在动态规划问题中的地位就等同于hello world

简单背包问题

问题描述: 给你一个可放总重量 W 的背包和 N 个物品，每个物品有重量 w 和价值 v 两个属性，第 i 个物品的重量是 w[i], 价值是 v[i], 现在让你用这个背包装物品，能装的最大价值是多少？

示例：

输入：


W = 5, N = 3
w = [3,2,1]
v = [5,2,3]


输出：8 选取第一个和最后一个物品，总重量不超过5，价值达到最大8

让我们先来分析一下，这是不是一个动态规划问题

在本系列的第一篇中，我提到了动态规划的三个特性，现在来回顾并分析一下

重叠子问题 光看题目，我们应该就能看出来，如果采用穷举的方式处理此问题，在不断回溯循环的过程中，肯定会涉及到大量的重复计算

无后效性 当我们选择了一个物品后，后续我们选择任意一个物品都不会对当前选择的物品的重量和价值产生任何影响

最优子结构 当我们做决策时，可以使用前面已经选择的物品以及计算出的重量和价值进行推算，即后续的计算可以通过前面的状态推导出来。

显而易见：此问题就是动态规划问题。

开始求解

这里我们再次回忆一下动态规划问题的处理过程：

我们处理动态规划问题的时候需要分为这么几步：

1）确定初始化状态，初始化状态作为整个求解链路的原点，需要优先明确；
2）状态参数，中间状态在一步一步推导出最终状态的过程中会发生变化的变量；
3）明确决策方式，即：如何通过前面的状态推导出后面的状态；
4）中间状态存储，子问题存在大量重复计算的情况，我们将中间状态存储入“备忘录”。

这道问题的初始化状态还是比较明显的就是当背包容量为0 或者没有任何物品可选的时候

状态参数：如题目中的描述，我们选择一个物品加入背包，物品的数量会增加，背包的剩余容量会减少，在这里选择哪几个物品，背包剩余容量就是变量即状态参数

决策方式：在本题目中，我们可以选择加入某个物品或者不加入某个物品，加入后，总价值和剩余容量会有个变化。这就是本题的决策方式。

中间状态存储：跟之前一样，依然是为了解决子问题的重复计算，我们需要开辟独立空间保存子问题的解。

分析完成，我们可以尝试着把状态决策转移的过程使用伪代码表示出来，以方便我们写出状态转移方程

DP(/**
    * 物品索引
    */
    int tn, 
    /**
     * 剩余容量
     **/
    int rw) {

    /**
     * 当遍历完所有物品时，就该返回 0 了，因为没有物品也就没有价值了
     **/
    if (tn < 0) 
        return 0;
    

    /**
     * 当背包还能容纳的重量已经小于当前物品的重量时，显然这个物品不能放入背包
     **/
    if (rw < w[tn]) 
        return dp(tn-1, rw);
    

    /**
     * 作出决策，该不该放入物品
     * 
     * 1. 放入：那么价值是 DP(tn - 1, rw - w[tn])+v[tn]；[表示总容量为rw-w[tn]的时候，前tn-1个遍历所得的结果，加上当前物品的价值]
     * 
     * 2. 不放入：那么价值是 DP(tn - 1, rw)。[表示总容量为rw的时候，前tn-1个遍历所得的结果]
     * 
     * 
     * 两者取最大值
     */
    return max(dp(tn - 1, rw), dp(tn - 1,rw - w[tn]) + v[tn]);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

分析到这里，我们大致可以写出状态转移方程了：

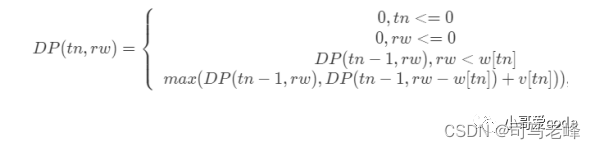
编写代码进行求解

到这里，我们可以编写代码进行求解了

这里有一个问题，这道题目中，有两个状态参数，我们需要设置一个二维数组来存储子问题的解。

我们设置其为DP[tn][rw], 其中行代表的是 tn，表示第几个物品；列代表的是 rw，表示背包还能容纳的重量。这个索引组合（比如 DP[2][3]）对应位置的值，就是这个子问题的答案，表示当背包还能容纳 3 的重量时，放入前 2 件物品的最大价值。

int dp(int[] w, int[] v, int N, int W) {
    // 创建备忘录
    int[][] dp = new int[N+1][W+1];
  
    // 初始化状态
    for (int i = 0; i < N + 1; i++) { dp[i][0] = 0; }
    for (int j = 0; j < W + 1; j++) { dp[0][j] = 0; }
  
    for (int tn = 1; tn < N + 1; tn++) { // 遍历每一件物品
    for (int rw = 1; rw < W + 1; rw++) { // 背包容量有多大就还要计算多少次
        if (rw < w[tn]) {
          // 当背包容量小于第tn件物品重量时，只能放入前tn-1件
          dp[tn][rw] = dp[tn-1][rw];
        } else {
                // 当背包容量还大于第tn件物品重量时，进一步作出决策
          dp[tn][rw] = Math.max(dp[tn-1][rw], dp[tn-1][rw-w[tn]] + v[tn]);
        }
      }
    }
  
  return dp[N][W];
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

到这里，我们本期要说的简单背包问题就分析完了，预告一下，下期分析完全背包问题！！

如果觉得本文有帮助可以分享给自己的小伙伴们！邀请他们关注下我的微信公众号

小哥爱code