力扣：第81场双周赛

6104. 统计星号

给你一个字符串 s ，每 两个 连续竖线 '|' 为 一对 。换言之，第一个和第二个 '|' 为一对，第三个和第四个 '|' 为一对，以此类推。

请你返回 不在 竖线对之间，s 中 '*' 的数目。

注意，每个竖线 '|' 都会 恰好 属于一个对。

示例 1：

输入：s = "l|*e*et|c**o|*de|"
输出：2
解释：不在竖线对之间的字符加粗加斜体后，得到字符串："l|*e*et|c**o|*de|" 。
第一和第二条竖线 '|' 之间的字符不计入答案。
同时，第三条和第四条竖线 '|' 之间的字符也不计入答案。
不在竖线对之间总共有 2 个星号，所以我们返回 2 。
1
2
3
4
5
6

提示：

• 1 <= s.length <= 1000
• s 只包含小写英文字母，竖线 '|' 和星号 '*' 。
• s 包含 偶数 个竖线 '|' 。

问题解析

可以一开始设一个flag：

• 当遇到的竖线数为奇数时，说明我们在一个竖线对之间，此时不记录‘*’的值。
• 当遇到的竖线数为偶数时，说明我们不在竖线对之间，此时可以记录‘ *’的值。

AC代码

class Solution {
public:
    int countAsterisks(string s) {
        int n=s.size(),res=0,cnt=0;
        for(int i=0;i<n;i++)
        {
            if(s[i]=='|')cnt++;
            else if(cnt%2==0&&s[i]=='*')res++;
        }
        return res;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12

6106. 统计无向图中无法互相到达点对数

给你一个整数 n ，表示一张 无向图 中有 n 个节点，编号为 0 到 n - 1 。同时给你一个二维整数数组 edges ，其中 edges[i] = [ai, bi] 表示节点 ai 和 bi 之间有一条 无向 边。

请你返回 无法互相到达 的不同 点对数目 。

示例 1：

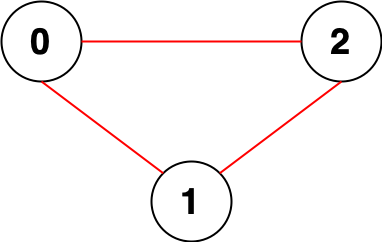
输入：n = 3, edges = [[0,1],[0,2],[1,2]]
输出：0
解释：所有点都能互相到达，意味着没有点对无法互相到达，所以我们返回 0 。
1
2
3

示例 2：

输入：n = 7, edges = [[0,2],[0,5],[2,4],[1,6],[5,4]]
输出：14
解释：总共有 14 个点对互相无法到达：
[[0,1],[0,3],[0,6],[1,2],[1,3],[1,4],[1,5],[2,3],[2,6],[3,4],[3,5],[3,6],[4,6],[5,6]]
所以我们返回 14 。
1
2
3
4
5

提示：

• 1 <= n <= 105
• 0 <= edges.length <= 2 * 105
• edges[i].length == 2
• 0 <= ai, bi < n
• ai != bi
• 不会有重复边。

问题解析

从样例2上我们就可以看出来了，只要不在一个连通块里的都不能叫互相到达，那么我们可以先根据路径把点都连成一个个连通块，再根据连通块的数量和节点数计算组合数。至于连成连通块只要用带记录点数的并查集就可以了。注意要压缩路径不然会t。

AC代码

class Solution {
public:
    int mysize[1000000],fa[1000000];
    int find(int x)
    {
        if(x!=fa[x])
            x=find(fa[x]);
        return fa[x];
    }
    long long countPairs(int n, vector<vector<int>>& edges) {
        for(int i=0;i<n;i++)fa[i]=i,mysize[i]=1;
        for(auto i:edges)
        {
            int a=i[0],b=i[1];
            int x=find(a),y=find(b);
            if(x!=y)
            {
                if(mysize[x]>mysize[y])swap(x,y);
                fa[x]=y;
                mysize[y]+=mysize[x];
            }
        }
        unordered_map<int,int>mymap;
        //res记录结果，ans记录遍历过的连通块的点
        long long res=0,ans=0;
        for(int i=0;i<n;i++)
        {
            int x=find(i);
            //如果当前连通块没有遍历到，就计算组合数
            if(mymap[x]==0)
            {
            	//当前连通块的点我们都视为遍历过
                ans+=mysize[x];
                //（n-ans）就是我们还没遍历到的其它连通块的节点数，这些节点对于当前这个连通块都是不可到达的
                res += (n - ans) * mysize[x];
                mymap[x]=1;
            }
        }
        return res;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

6105. 操作后的最大异或和

给你一个下标从 0 开始的整数数组 nums 。一次操作中，选择 任意 非负整数 x 和一个下标 i ，更新 nums[i] 为 nums[i] AND (nums[i] XOR x) 。

注意，AND 是逐位与运算，XOR 是逐位异或运算。

请你执行 任意次 更新操作，并返回 nums 中所有元素 最大 逐位异或和。

示例 1：

输入：nums = [3,2,4,6]
输出：7
解释：选择 x = 4 和 i = 3 进行操作，num[3] = 6 AND (6 XOR 4) = 6 AND 2 = 2 。
现在，nums = [3, 2, 4, 2] 且所有元素逐位异或得到 3 XOR 2 XOR 4 XOR 2 = 7 。
可知 7 是能得到的最大逐位异或和。
注意，其他操作可能也能得到逐位异或和 7 。
1
2
3
4
5
6

示例 2：

输入：nums = [1,2,3,9,2]
输出：11
解释：执行 0 次操作。
所有元素的逐位异或和为 1 XOR 2 XOR 3 XOR 9 XOR 2 = 11 。
可知 11 是能得到的最大逐位异或和。
1
2
3
4
5

提示：

• 1 <= nums.length <= 10^5
• 0 <= nums[i] <= 10^8

问题解析

异或运算的性质是：二进制下，相同位置上的数相同则为0，不相同则为1。

这就说明了，如果想要通过异或运算得到一个尽可能大的值，那么二进制下每个位置上1的数量应该是奇数。比如2（10）和1（01）异或运算，二进制下第一个位置和第二个位置上的1都是只有1个；如果是2（10）和3（11），那么第一个位置上1的个数是奇数，第二个位置上就是偶数了。

和运算的性质是：二进制下，相同位置上的数都是1则为1，其它情况都是0。

题目说了可以任意次操作，那么如果某个位置上的1数量为偶数时（不为0），我们可以通过and运算来把那个位置变成奇数（只要把某个二进制下该位置为1的数and一个除了这个位置为0其它全是1的数即可）。

也就是说，进行异或运算，每个位置的1我们能是奇数都是奇数（如果为0就没办法了），记录下这些1的位置，再转成十进制数就是我们要的结果了。

例如：3（11），2（10），4（100），6（110）。此时第一个位置上1的数量是1，第二个位置是3，第三个位置是2，那我们通过and运算把第三个位置减少一个1，这样最后异或运算得到的二进制数就是：111。转成十进制就是7.

AC代码

class Solution {
public:
    map<int,int>mymap;
    int maximumXOR(vector<int>& nums) {
        int n=nums.size(),res=0;
        //v先存下2的0~30次幂
        vector<int>v(31,1);
        for(int i=1;i<31;i++)
        {
            v[i]=v[i-1]*2;
        }
        //对所有数求一边二进制
        for(int i=0;i<n;i++)
        {
            int x=nums[i],cnt=0;
            while(x)
            {
            	//这个位置如果为1，那就加到我们的结果里，注意每个位置的数只能取一次，取完后这个位置的数清0
                if(x%2==1)res+=v[cnt],v[cnt]=0;
                cnt++;
                x/=2;
            }
        }

        return res;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

6107. 不同骰子序列的数目

给你一个整数 n 。你需要掷一个 6 面的骰子 n 次。请你在满足以下要求的前提下，求出 不同 骰子序列的数目：

序列中任意 相邻 数字的 最大公约数 为 1 。
序列中 相等 的值之间，至少有 2 个其他值的数字。正式地，如果第 i 次掷骰子的值 等于 第 j 次的值，那么 abs(i - j) > 2 。
请你返回不同序列的 总数目 。由于答案可能很大，请你将答案对 10^ 9 + 7 取余 后返回。

如果两个序列中至少有一个元素不同，那么它们被视为不同的序列。

示例 1：

输入：n = 4
输出：184
解释：一些可行的序列为 (1, 2, 3, 4) ，(6, 1, 2, 3) ，(1, 2, 3, 1) 等等。
一些不可行的序列为 (1, 2, 1, 3) ，(1, 2, 3, 6) 。
(1, 2, 1, 3) 是不可行的，因为第一个和第三个骰子值相等且 abs(1 - 3) = 2 （下标从 1 开始表示）。
(1, 2, 3, 6) i是不可行的，因为 3 和 6 的最大公约数是 3 。
总共有 184 个不同的可行序列，所以我们返回 184 。
1
2
3
4
5
6
7
8
9

提示：

• 1 <= n <= 104

问题解析

设一个n*6 *6的三维数组f，f[i] [last] [last2]的意思是：长度为i的序列，且最后一个数是last，倒数第二个数是last2的序列

有f[i] [last] [last2]个。

然后我们扩展至长度为i+1的序列时，枚举添加到尾部的数是j，即f[i+1] [j] [last]

因为last和j是相邻情况，所以j!=last,而且gcd(j,last)==1。

同时last2也不能等于j，因为此时j和last2的位置只相隔一个数，不满足条件。

状态转移方程即为：f[i+1] [j] [last]=(f[i+1] [j] [last] + f[i] [last] [last2])%MOD;

最后只要枚举i和j的数把f[n] [i] [j]的值全部加起来，就是长度为n的序列的种类数了。

AC代码

class Solution {
public:
    int MOD=1e9+7;
    int gcd(int a,int b)
    {
        return a==0?b:gcd(b%a,a);
    }
    int distinctSequences(int n) {
        vector<vector<vector<long long>>>v(n+1,vector<vector<long long>>(7,vector<long long>(7)));
        if(n==1)return 6;
        for(int i=1;i<=6;i++)
            for(int j=1;j<=6;j++)
                if(i!=j&&gcd(i,j)==1)
                    v[2][i][j]++;
        for(int i=2;i<n;i++)
            for(int j=1;j<=6;j++)
                for(int last=1;last<=6;last++)
                    if(j!=last&&gcd(j,last)==1)
                        for(int last2=1;last2<=6;last2++)    
                            if(last2!=j)                          
                                v[i + 1][j][last] = (v[i + 1][j][last] + v[i][last][last2]) % MOD;
        long long res=0;
        for(int i=1;i<=6;i++)
            for(int j=1;j<=6;j++)
                res+=v[n][i][j];                    
        return res%MOD;               
                 
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29