三十九、字符串类的创建（上）

1、历史遗留问题

• C语言不支持真正意义上的字符串
• C语言用字符数组和一组函数实现字符串操作
• C语言不支持自定义类型，因此无法获得字符串类型
• 从C到C++的进化过程引入了自定义类型
• 在C++中可以通过类完成字符串类型的定义
  • 问题：

C++中的原生类型系统是否包含字符串类型？

没有，通过标准库。

2、DTLib 中字符串类的设计

3、DTLib 中字符串类的实现

        

4、实现时的注意事项

• 无缝实现 String对象与char*字符串的互操作
• 操作符重载函数需要考虑是否支持const版本
• 通过C语言中的字符串函数实现String的成员函数

5、编程实验：字符串类的实现

String.h

String.cpp

6、小结

• C /C+＋语言本身不支持字符串类型
• C语言通过字符数组和一组函数支持字符串操作
• C++通过自定义字符串类型支持字符串操作
• 字符串类型通过C语言中的字符串函数实现

四十、字符串类的创建（下）

1、字符串类中的常用成员函数

2、重载数组访问操作符[]

• char& operator [] (int i);
• char operator [] (int i) const;
• 注意事项
  • 当i的取值不合法时，抛出异常
    • 合法范围：( 0<=i ) && ( i < m_length )

3、判断是否以指定字符串开始或结束

• bool startWith(const char* s) const;
• bool startWith(const String& s) const;
• bool endOf(const char* s) const;
• bool endOf(const String& s) const;

4、在指定位置处插入字符串

• String& insert(int i, const char* s);
• String& insert(int i, const String& s);

5、去掉字符串两端的空白字符

• String & trim();

6、编程实验：常用成员函数的实现

string.h

string.cpp

7、To be continued ...

思考：

如何在目标字符串中查找是否存在指定的子串？

四十一、KMP 子串查找算法

1、问题

如何在目标字符串S中，查找是否存在子串P ？

2、朴素解法

3、朴素解法的一个优化线索

4、示例

5、伟大的发现

• 匹配失败时的右移位数与子串本身相关，与目标串无关
• 移动位数 = 已匹配的字符数 - 对应的部分匹配值
• 任意子串都存在一个唯一的部分匹配表

6、部分匹配表示例

7、问题：部分匹配表是怎么得到的？

• 前缀
  • 除了最后一个字符以外，一个字符串的全部头部组合
• 后缀
  • 除了第一个字符以外，一个字符串的全部尾部组合
• 部分匹配值
  • 前缀和后缀最长共有元素的长度

示例: ABCDABD

8、问题：怎么编程产生部分匹配表？

• 实现关键
  • PMT[1] = 0（下标为0的元素匹配值为0）
  • 从2个字符开始递推（从下标为1的字符开始递推）
  • 假设PMT[n] = PMT[n-1]+1（最长共有元素的长度）
  • 当假设不成立，PMT[n]在PMT[n-1]的基础上减小

9、编程实验：部分匹配表的递推与实现

10、部分匹配表的使用（KMP算法）

11、编程实验：KMP子串查找算法的实现

12、小结

• 部分匹配表是提高子串查找效率的关键
• 部分匹配值定义为前缀和后缀最长共有元素的长度
• 可以用递推的方法产生部分匹配表
• KMP利用部分匹配值与子串移动位数的关系提高查找效率

四十二、KMP 算法的应用

1、思考

如何在目标字符串中查  找是否存在指定的子串？

2、字符串类中的新功能

3、子串查找（KMP算法的直接运用）

• int indexOf(const char* s) const
• int indexOf(const String& s) const

4、在字符串中将指定的子串删除

• String& remove(const char* s)
• String& remove(const String& s)
  1. 根据KMP在目标字符串中查找子串的位置
  2. 通过子串位置和子串长度进行删除

5、字符串的减法操作定义（ operator - ）

• 使用remove实现字符串间的减法操作
  • 字符串自身不被修改
  • 返回产生的新串

6、字符串中的子串替换

• String& replace(const char* t, const char* s)
• String& replace(const String& t, const char* s)
• String& replace(const char* t, const String& s)
• String& replace(const String& t, const String& s)

7、从字符串中创建子串

• String sub(int i, int len) const
  • 以i为起点提取长度为len的子串
  • 子串提取不会改变字符串本身的状态

8、编程实验：新成员函数的实现

string.h

string.cpp

9、小结

• 字符串类是工程开发中必不可少的组件
• 字符串中应该包含常用字符串操作函数
  • 增：insert , operator + , .….
  • 删：remove , operator -, …
  • 查：indexOf , ...
  • 改：replace , ...

补充、字符串匹配算法

1、BF算法，Brute Force（暴力算法）

第一轮，从主串的首位开始，把主串和模式串的字符逐个比较：

显然，主串的首位字符是a，模式串的首位字符是b，两者并不匹配。

第二轮，把模式串后移一位，从主串的第二位开始，把主串和模式串的字符逐个比较：

主串的第二位字符是b，模式串的第二位字符也是b，两者匹配，继续比较：

主串的第三位字符是b，模式串的第三位字符也是c，两者并不匹配。

第三轮，把模式串再次后移一位，从主串的第三位开始，把主串和模式串的字符逐个比较：

主串的第三位字符是b，模式串的第三位字符也是b，两者匹配，继续比较：

主串的第四位字符是c，模式串的第四位字符也是c，两者匹配，继续比较：

主串的第五位字符是e，模式串的第五位字符也是e，两者匹配，比较完成！

由此得到结果，模式串 bce 是主串 abbcefgh 的子串，在主串第一次出现的位置下标是 2：

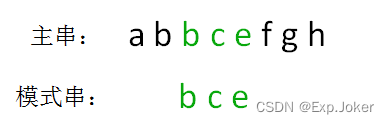
假设主串的长度是m，模式串的长度是n，那么在这种极端情况下，BF算法的最坏时间复杂度是O（mn）。

 

2、RK 算法

全称Rabin-Karp，是由算法的两位发明者Rabin和Karp的名字来命名的。

① RK 算法的核心

BF算法只是简单粗暴地对两个字符串的所有字符依次比较，而RK算法比较的是两个字符串的[哈希值]。

每一个字符串都可以通过某种哈希算法，转换成一个整型数，这个整型数就是hashcode：

hashcode = hash（string）

② RK 算法的推演

给定主串和模式串如下（假定字符串只包含26个小写字母）：

第一步，需要生成模式串的hashcode。

生成hashcode的算法多种多样，比如：

方法一：按位相加

这是最简单的方法，可以把a当做1，b当做2，c当做3......然后把字符串的所有字符相加，相加结果就是它的hashcode。

bce =  2 + 3 + 5 = 10

但是，这个算法虽然简单，却很可能产生hash冲突，比如bce、bec、cbe的hashcode是一样的。

方法二：转换成26进制数

既然字符串只包含26个小写字母，那么可以把每一个字符串当成一个26进制数来计算。

bce = 2*(26^2) + 3*26 + 5 = 1435

这样做的好处是大幅减少了hash冲突，缺点是计算量较大，而且有可能出现超出整型范围的情况，需要对计算结果进行取模。

 

后续采用的是按位相加的hash算法，所以bce的hashcode是10：

第二步，生成主串当中第一个等长子串的hashcode。

由于主串通常要长于模式串，把整个主串转化成hashcode是没有意义的，只有比较主串当中和模式串等长的子串才有意义。

因此，首先生成主串中第一个和模式串等长的子串hashcode，

即abb = 1 + 2 + 2 = 5：

第三步，比较两个hashcode。

显然，5！=10，说明模式串和第一个子串不匹配，继续下一轮比较。

第四步，生成主串当中第二个等长子串的hashcode。

bbc = 2 + 2 + 3 = 7：

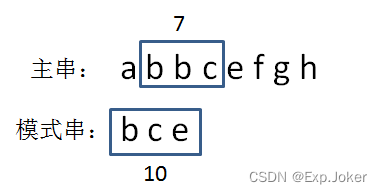
第五步，比较两个hashcode。

显然，7！=10，说明模式串和第二个子串不匹配，继续下一轮比较。

第六步，生成主串当中第三个等长子串的hashcode。

bce= 2 + 3 + 5 = 10：

第七步，比较两个hashcode。

显然，10 ==10，两个hash值相等！这是否说明两个字符串也相等呢？

别高兴的太早，由于存在hash冲突的可能，还需要进一步验证。

第八步，逐个字符比较两字符串。

hashcode的比较只是初步验证，之后还需要像BF算法那样，对两个字符串逐个字符比较，最终判断出两个字符串匹配。

最后得出结论，模式串bce是主串abbcefgh的子串，第一次出现的下标是2。

③ RK 算法的优化

每次hash的时间复杂度是0(n)，如果把全部子串都进行hash，总的时间复杂度是0(mn)。

解决方法：对子串的hash计算并不是独立的，从第二个子串开始，每一个子串的 hash都可以由上一个子串进行简单的增量计算来得到：

上图中，我已知子串abbcefg的hashcode是26，那么如何计算下一个子串，也就是bbcefgd的hashcode呢？

由于新子串的前面少了一个a，后面多了一个d，所以：

新hashcode = 旧hashcode - 1 + 4 = 26-1+4 = 29 

再下一个子串bcefgde的计算也是同理：

新hashcode = 旧hashcode - 2 + 5 = 29-2+5 = 32

④ RK 算法代码实现

 

⑤ RK 算法时间复杂度

RK算法计算单个子串hash 的时间复杂度是0 (n)，但由于后续的子串hash是增量计算，所以总的时间复杂度仍然是0 (n)。

⑥ RK 算法缺点

RK算法的缺点在于哈希冲突。每一次哈希冲突的时候，RK算法都要对子串和模式串进行逐个字符的比较,如果冲突太多了，算法就退化成了BF算法。

3、BM 算法

BM算法的名字取自于它的两位发明者，计算机科学家Bob Boyer和JStrother Moore。

① BM 算法的核心

采用字符比较的思路，并且尽量减少无谓的比较，这就是BM算法的努力方向。

为了能减少比较，BM算法制定了两条规则，一个是[坏字符规则]，一个是[好后缀规则]。

坏字符规则

② BM 算法 - 坏字符规则 推演

“坏字符” 是什么意思？就是指模式串和子串当中不匹配的字符。

当模式串和主串的第一个等长子串比较时，子串的最后一个字符T就是坏字符：

为什么坏字符不是主串第2位的字符T呢？那个位置不是最先被检测到的吗？

BM算法的检测顺序相反，是从字符串的最右侧向最左侧检测。

当检测到第一个坏字符之后，只有模式串与坏字符T对齐的位置也是字符T的情况下，两者才有匹配的可能。

模式串的第1位字符也是T，直接把模式串当中的字符T和主串的坏字符对齐，进行下一轮的比较：

坏字符的位置越靠右，下一轮模式串的挪动跨度就可能越长，节省的比较次数也就越多。这就是BM算法从右向左检测的好处。

接下来，继续逐个字符比较，发现右侧的G、C、G都是一致的，但主串当中的字符A，是又一个坏字符：

按照刚才的方式，找到模式串的第2位字符也是A，于是我们式串的字符A和主串中的坏字符对齐，进行下一轮比较：

接下来，继续逐个字符比较，这次发现全部字符都是匹配的，比较公正完成：

如果坏字符在模式串中不存在，又该如何挪动呢？

直接把模式串挪到主串坏字符的下一位：

③ BM 算法 - 坏字符规则 代码实现

BM算法的[阉割版]（坏字符规则只是BM算法的两大法宝之一，除此之外它还具备另一件法宝:[好后缀规则]。）

好后缀规则

④ BM 算法 - 好后缀规则 推演

“好后缀” 又是什么意思？就是指模式串和子串当中相匹配的后缀。

对于上面的例子，如何继续使用“坏字符规则”，会有怎样的效果呢？

从后向前比对字符，发现后面三个字符都是匹配的，到了第四个字符的时候，发现坏字符G：

接下来在模式串找到了对应的字符G，但是按照坏字符规则，模式串仅仅能够向后挪动一位：

这时候坏字符规则显然并没有起到作用，为了能真正减少比较次数，轮到好缀规则出场了。

回到第一轮的比较过程，发现主串和模式串都有共同的后缀“GCG”，这就是所谓的“好后缀”。

如果模式串其他位置也包含与“GCG”相同的片段，那么就可以挪动模式串，让这个片段和好后缀对齐，进行下一轮的比较：

显然，在这个例子中，采用好后缀规则能够让模式串向后移动更多位，节省了更多无谓的比较。

那么，如果模式串当中并不存在其他与好后缀相同的片段，该怎么处理？是不是可以直接把模式串挪到好后缀之后？

不能直接挪动模式串到好后缀的后面，还要先判断一种特殊情况：

模式串的前缀是否和好后缀的后缀相匹配，免得挪过头了。

 

⑤ 在什么情况下应该使用坏字符规则，什么情况下应该使用好后缀规则呢？

举个例子，假设坏字符规则可以让模式串在下一轮挪动3位，好后缀规则可以让模式串在下一轮挪动5位，那就采用好后缀规则。

在每一轮的字符比较之后，按照坏字符和好后缀规则分别计算相应的挪动距离，哪一种距离更长，就把模式串挪动对应的长度。

⑥ BM 算法 - 好后缀规则 代码实现

四十三、递归的思想与应用（上）

1、递归是一种数学上分而自治的思想

• 将原问题分解为规模较小的问题进行处理
  • 分解后的问题与原问题的类型完全相同，但规模较小
  • 通过小规模问题的解，能够轻易求得原问题的解
• 问题的分解是有限的（递归不能无限进行）
  • 当边界条件不满足时，分解问题（递归继续进行）
  • 当边界条件满足时，直接求解（递归结束）

2、递归模型的一般表示法

3、递归在程序设计中的应用

• 递归函数
  • 函数体中存在自我调用的函数
  • 递归函数必须有递归出口（边界条件）
  • 函数的无限递归将导致程序崩溃

4、递归思想的应用

5、编程实验：递归求和

unsigned int sum(unsigned int n);

6、斐波拉契数列

数列自身递归定义：1，1，2，3，5，8，13，21，...

7、编程实验：斐波拉契数列

unsigned int Fibonacci(unsigned int n);

8、用递归的方法编写函数求字符串长度

9、编程实验：求字符串长度

unsigned int strlen(const char* s);

10、小结

• 递归是一种将问题分而自治的思想
• 用递归解决问题首先要建立递归的模型
• 递归解法必须要有边界条件，否则无解
• 不要陷入递归函数的执行细节，学会通过代码描述递归问题

四十四、递归的思想与应用（中）

1、单向链表的转置

2、编程实验：单向链表的转置

Node* reverse(Node* list)

3、单向排序链表的合并

4、编程实验：单向排序链表的合并

Node* merge(Node* list1, Node* list2)

5、汉诺塔问题

• 将木块借助B柱由A柱移动到C柱
• 每次只能移动一个木块
• 只能出现小木块在大木块之上

6、汉诺塔问题分解

• 将n-1个木块借助C柱由A柱移动到B柱
• 将最底层的唯一木块直接移动到C柱
• 将n-1个木块借助A柱由B柱移动到C柱

7、编程实验：汉诺塔问题求解

void HanoiTower(int n, char a, char b, char c)

8、全排列问题

9、编程实验：全排列的递归解法

void permutation(char* s)

10、小提示

递归还能用于需要回溯穷举的场合。

四十五、递归的思想与应用（下）

1、函数调用过程回顾

• 程序运行后有一个特殊的内存区供函数调用使用
  • 用于保存函数中的实参，局部变量，临时变量，等
  • 从起始地址开始往一个方向增长（如：高地址→低地址）
  • 有一个专用“指针”标识当前已使用内存的”顶部”

2、程序中的栈区：一段特殊的专用内存区

3、实例分析：逆序打印单链表中的偶数结点

4、编程实验：函数调用栈分析

void r_print_even(Node* list)

5、八皇后问题

在一个8×8的国际象棋棋盘上，有8个皇后，每个皇后占一格;要求皇后间不会出现相互“攻击”的现象

（不能有两个皇后处在同一行、同一列或同一对角线上）。

6、关键数据结构定义

• 棋盘：二维数组( 10 * 10 )
  • 0表示位置为空，1表示皇后，2表示边界
• 位置：struct Pos;
  • 
• 方向
  • 水平：(-1,0),(1,0)
  • 垂直：(0,-1),(0,1)
  • 对角线：(-1,1),(-1,-1),(1,-1),(1,1)

7、算法思路

1.初始化：j = 1

2.初始化：i = 1

3.从第j行开始，恢复 i 的有效值（通过函数调用栈进行回溯），判断第i个位置

a. 位置i可放入皇后：标记位置(i,j)， j++，转步骤2

b. 位置i不可放入皇后：i++，转步骤a

c. 当i>8时，j--，转步骤3

结束：

第8行有位置可放入皇后

8、编程实验：八皇后问题的递归解法

class QueueSolution;

9、小结

• 程序运行后的栈存储区专供函数调用使用
• 栈存储区用于保存实参，局部变量，临时变量，等
• 利用栈存储区能够方便的实现回溯算法
• 八皇后问题是栈回溯的经典应用