---

题目一

给定一个非负数组arr，长度为N，
那么有N-1种方案可以把arr切成左右两部分
每一种方案都有，min{左部分累加和，右部分累加和}
求这么多方案中，min{左部分累加和，右部分累加和}的最大值是多少？
整个过程要求时间复杂度O(N)

解题思路

先求全局累加和,左部分不断往右扩

代码

	public static int bestSplit(int[] arr) {
		if (arr == null || arr.length < 2) {
			return 0;
		}
		int N = arr.length;
		int sumAll = 0;
		for (int num : arr) {
			sumAll += num;
		}
		int ans = 0;
		int sumL = 0;
		// [0...s]  [s+1...N-1]
		for (int s = 0; s < N - 1; s++) {
			sumL += arr[s];
			int sumR = sumAll - sumL;
			ans = Math.max(ans, Math.min(sumL, sumR));
		}
		return ans;
	}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

题目二

把题目一中提到的，
min{左部分累加和，右部分累加和}，定义为S(N-1)，也就是说：
S(N-1)：在arr[0…N-1]范围上，做最优划分所得到的min{左部分累加和，右部分累加和}的最大值
现在要求返回一个长度为N的s数组，
s[i] =在arr[0…i]范围上，做最优划分所得到的min{左部分累加和，右部分累加和}的最大值
得到整个s数组的过程，做到时间复杂度O(N)

解题思路

暴力解:所有位置划分点都尝试一遍

	public static int[] bestSplit1(int[] arr) {
		if (arr == null || arr.length == 0) {
			return new int[0];
		}
		int N = arr.length;
		int[] ans = new int[N];
		ans[0] = 0;
		for (int range = 1; range < N; range++) {
			for (int s = 0; s < range; s++) {
				int sumL = 0;
				for (int L = 0; L <= s; L++) {
					sumL += arr[L];
				}
				int sumR = 0;
				for (int R = s + 1; R <= range; R++) {
					sumR += arr[R];
				}
				ans[range] = Math.max(ans[range], Math.min(sumL, sumR));
			}
		}
		return ans;
	}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

不回退的解法
在求上一个区间的时候,存在着一个最好的划分点,在求现在的区间的时候,该划分点只会往右移,不会往左退

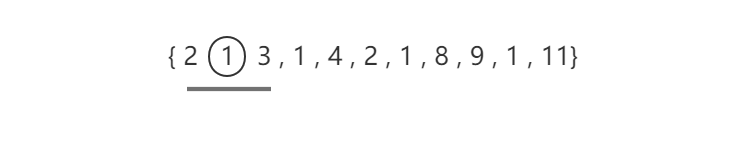
如图,在0-3的区间内,最佳划分点为1位置,那么在求0-4位置,最佳划分点要么不变,要么右移,因为往左移的话,左区间的值会变小,右区间的值会变大,最终答案会变小
我们尝试让划分点往右移,如果让答案变大,那么右移,如果变小或者不变,那么保持不动

	public static int sum(int[] sum, int L, int R) {
		return sum[R + 1] - sum[L];
	}

	public static int[] bestSplit3(int[] arr) {
		if (arr == null || arr.length == 0) {
			return new int[0];
		}
		int N = arr.length;
		int[] ans = new int[N];
		ans[0] = 0;
		int[] sum = new int[N + 1];
		for (int i = 0; i < N; i++) {
			sum[i + 1] = sum[i] + arr[i];
		}
		// 最优划分
		// 0~range-1上，最优划分是左部分[0~best]  右部分[best+1~range-1]
		int best = 0;
		for (int range = 1; range < N; range++) {
			while (best + 1 < range) {
				int before = Math.min(sum(sum, 0, best), sum(sum, best + 1, range));
				//最好划分点右移
				int after = Math.min(sum(sum, 0, best + 1), sum(sum, best + 2, range));
				if (after >= before) {
					best++;
				} else {
					break;
				}
			}
			ans[range] = Math.min(sum(sum, 0, best), sum(sum, best + 1, range));
		}
		return ans;
	}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

不回退的技巧

ans=max{min{左,右}}
ans=min{max{左,右}}
每个位置上的答案,如果满足上面公式,存在不回退抽象化,以后可能都存在不回退现象
只要你发现指标跟区间之间存在单调性,它又是一个类似于这样范式和把最优放外头把最差放里面的情况,可能都存在不回退现象,不需要去证明,用对数器去验证即可

题目三

摆放着n堆石子。现要将石子有次序地合并成一堆
规定每次只能选相邻的2堆石子合并成新的一堆，
并将新的一堆石子数记为该次合并的得分
求出将n堆石子合并成一堆的最小得分合并方案

解题思路

考虑一个问题:
arr从L.R范围上怎么合并最优?
枚举最后一刀
中间划分点的位置左部分跟右部分全试一遍,那么从L到R的最优划分总在其中。
范围上的尝试的动态规划模型
定义dp[L][R]:arr 在L到R范围里最优划分情况下,最优合并方案情况下的最小代价
先看对角线,dp[i][i]:只有一个数,因此都为0

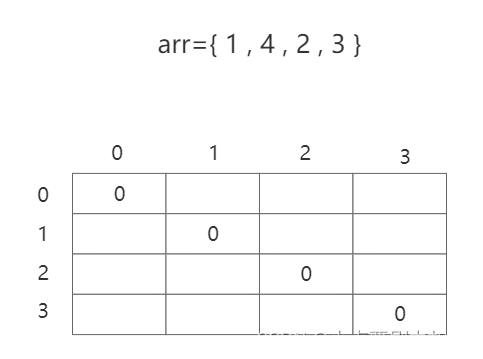
我们再看第二条对角线怎么填,dp[0][1]:即arr在0到1范围怎么合并,只有一种合并方法,两个数相加,
因此dp[0][1]=5,同理dp[1][2]=6,dp[2][3]=5

那么dp[1][3]怎么填
看最后一刀怎么砍,砍在1-2之间合并代价最小
先把[1,1]合并了,然后再[2,3]合你看怎么最少,最后加上123整体的累加和
即dp[1][1]+dp[2][3]+sum(1,3);
那么dp[0][2]怎么填
我们枚举最后一刀在0-1位置和最后一刀在1-2位置,看哪种情况最优
dp[0][0]+dp[1][2]+sum(0,2)
dp[0][1]+dp[2][2]+sum(0,2)
取二者中的最小值
所以剩下的格子从左往右再从下往上推到顶格,最后求出我们要的解[0,3]范围上整体答案是什么

	public static int process1(int L, int R, int[] s) {
		if (L == R) {
			return 0;
		}
		int next = Integer.MAX_VALUE;
		for (int leftEnd = L; leftEnd < R; leftEnd++) {
			next = Math.min(next, process1(L, leftEnd, s) + process1(leftEnd + 1, R, s));
		}
		return next + w(s, L, R);
	}

	public static int min2(int[] arr) {
		if (arr == null || arr.length < 2) {
			return 0;
		}
		int N = arr.length;
		int[] s = sum(arr);
		int[][] dp = new int[N][N];
		// dp[i][i] = 0
		for (int L = N - 2; L >= 0; L--) {
			for (int R = L + 1; R < N; R++) {
				int next = Integer.MAX_VALUE;
				// dp(L..leftEnd)  + dp[leftEnd+1...R]  + 累加和[L...R]
				for (int leftEnd = L; leftEnd < R; leftEnd++) {
					next = Math.min(next, dp[L][leftEnd] + dp[leftEnd + 1][R]);
				}
				dp[L][R] = next + w(s, L, R);
			}
		}
		return dp[0][N - 1];
	}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

假设我现在正在求L等于3,R等于17位置的格子的解。
正常来讲你是需要枚举所有划分点的。
3-3是左部分4-17右部分
3-4是左部分5-17右部分
3-5是左部分6-17右部分
3-6是左部分7-17右部分
尝试所有求解的顺序是,从底层从左往右依次从下往上求的。所以当我求这个格子的时候,我左边的格子已经求过了。
左边可是代表3-16范围上怎么和最优,下面格代表4-17范围上怎么和最优
我左侧3-16的问题,假设它的最优划分点在8-9之间
我下面的格子4-17这个问题上,它的最优划分点12-13之间。
如果我能够证明我在左侧不用越过8以左,我在右侧不用越过13以右我的枚举行为将大大简化。
我只用试划分点8-9,9-10, 11-12, 12-13可以了。别的什么划分位置我都不试,我的左边跟我的下方,如果能够给我一个尝试的下限和一个尝试的上限,我的枚举行为将得到大量的改进。

	public static int min3(int[] arr) {
		if (arr == null || arr.length < 2) {
			return 0;
		}
		int N = arr.length;
		int[] s = sum(arr);
		int[][] dp = new int[N][N];
		int[][] best = new int[N][N];
		for (int i = 0; i < N - 1; i++) {
			best[i][i + 1] = i;
			dp[i][i + 1] = w(s, i, i + 1);
		}
		for (int L = N - 3; L >= 0; L--) {
			for (int R = L + 2; R < N; R++) {
				int next = Integer.MAX_VALUE;
				int choose = -1;
				for (int leftEnd = best[L][R - 1]; leftEnd <= best[L + 1][R]; leftEnd++) {
					int cur = dp[L][leftEnd] + dp[leftEnd + 1][R];
					if (cur <= next) {
						next = cur;
						choose = leftEnd;
					}
				}
				best[L][R] = choose;
				dp[L][R] = next + w(s, L, R);
			}
		}
		return dp[0][N - 1];
	}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

四边形不等式优化特征

1，两个可变参数的区间划分问题
2，每个格子有枚举行为
3，当两个可变参数固定一个，另一个参数和答案之间存在单调性关系
4，而且两组单调关系是反向的：(升 升，降 降) (升 降，降 升)
5，能否获得指导枚举优化的位置对：上+右，或者，左+下

那么我们看上一题
符合1和2特征
当两个可变参数固定另外一个参数和答案之间存在单调性关系。
例如我要在3-17上做最优划分,让它合并代价最小。
当我固定17,你看一下4-17范围上的合并代价恐怕不会比3-17的合并代价高.范围变小和合并代价只会变小或不变。
2-17范围上,范围变大了,恐怕它合并代价不会比原始问题更少。
因此固定右边的数,划分点向右移,代价变小,向左移,代价变大,符合(升 升，降 降)
当我固定3时,同理,划分点向右移,代价变大,划分点向左移,代价变小.,符合(升 降，降 升)。
因此符合特征3和4
在求解过程中,我们发现能获得指导枚举优化的位置对:左+下,符合特征5
符合这前五个特征的不用证明。就写对数器验证。你验证出来你就用,你没验出来那就不存在。大不了不用它。

410. 分割数组的最大值

给定一个非负整数数组 nums 和一个整数 m ，你需要将这个数组分成 m 个非空的连续子数组。

设计一个算法使得这 m 个子数组各自和的最大值最小。

示例 1：

输入：nums = [7,2,5,10,8], m = 2
输出：18
解释：
一共有四种方法将 nums 分割为 2 个子数组。
其中最好的方式是将其分为 [7,2,5] 和 [10,8] 。
因为此时这两个子数组各自的和的最大值为18，在所有情况中最小。

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/split-array-largest-sum

解题思路

题目含义为把数组分为k份,哪种情况下,最大部分的累加和最小
尝试模型:一个样本做行一个样本做列
dp[i][j]:代表arr从0到i这些位置必须切割j份,j个子数组累加和的最大值最小情况是多少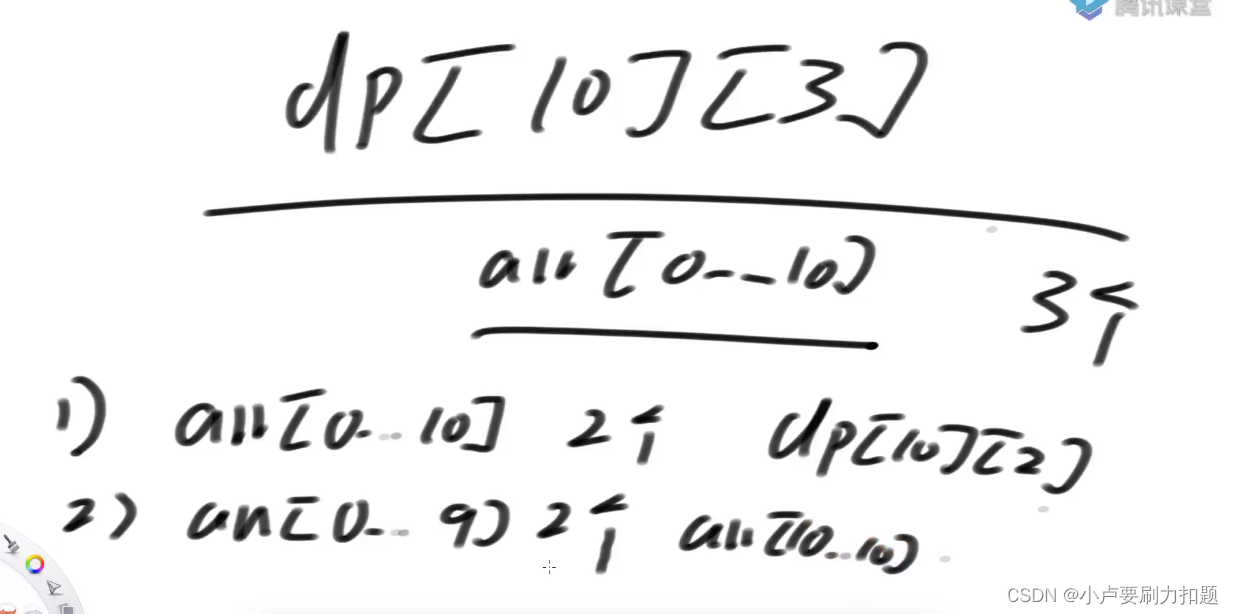

例如,dp[10][3]:枚举最后一个子数组的范围
1)arr[0-10]分为2部分,最后一个部分没有
2)arr[0-9]分为2部分,最后一个部分为arr[10]
3)arr[0-8]由1个切割点负责,最后一个部分为arr[9-10]
…

0位置:arr[0]只有一个元素,0个子数组,不填
第一行都是arr[0],只有一个元素,再多的子数组没有用,填arr[0]
第一列全是X, 0个子数组没法算
第二列arr[0,1,2,3…],一个子数组,累加和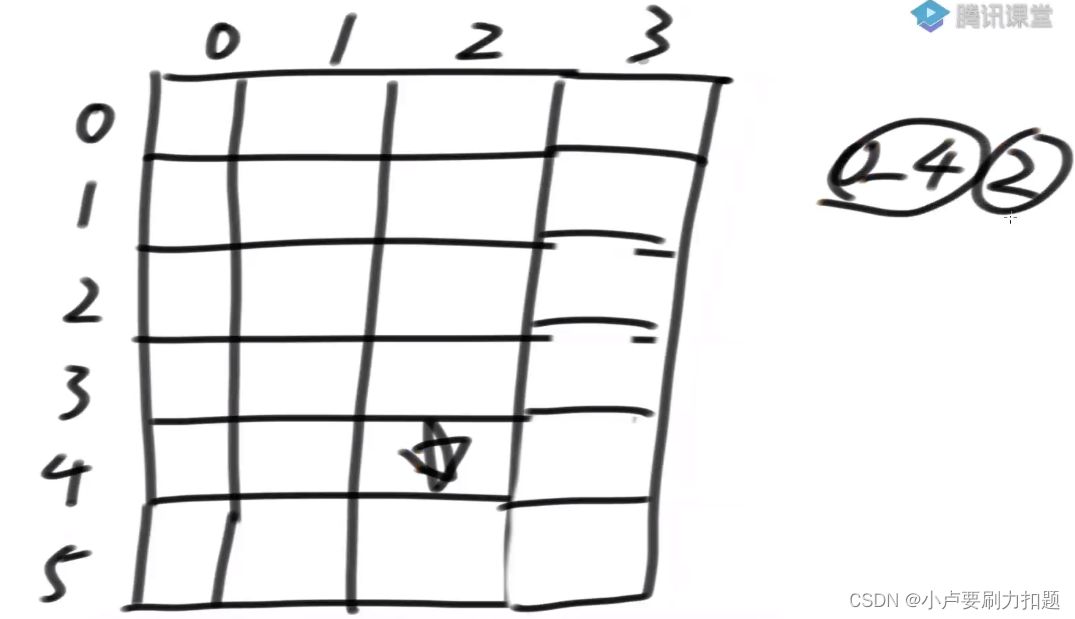

我们看普遍位置:
dp[4][2]:0-4位置,分成2个子数组

0-4范围只分为1个子数组,最后一个子数组为空
0-3范围只分为1个子数组,最后一个子数组负责4位置
0-2范围只分为1个子数组,最后一个子数组负责3-4
0-1范围只分为1个子数组,最后一个子数组负责2-4
0-0范围只分为1个子数组,最后一个子数组负责1-4
因此星号依赖自己左侧的一列

	// 求原数组arr[L...R]的累加和
	public static int sum(int[] sum, int L, int R) {
		return sum[R + 1] - sum[L];
	}

	// 不优化枚举的动态规划方法，O(N^2 * K)
	public static int splitArray1(int[] nums, int K) {
		int N = nums.length;
		int[] sum = new int[N + 1];
		for (int i = 0; i < N; i++) {
			sum[i + 1] = sum[i] + nums[i];
		}
		int[][] dp = new int[N][K + 1];
		for (int j = 1; j <= K; j++) {
			dp[0][j] = nums[0];
		}
		for (int i = 1; i < N; i++) {
			dp[i][1] = sum(sum, 0, i);
		}
		// 每一行从上往下
		// 每一列从左往右
		// 根本不去凑优化位置对儿！
		for (int i = 1; i < N; i++) {
			for (int j = 2; j <= K; j++) {
				int ans = Integer.MAX_VALUE;
				// 枚举是完全不优化的！
				for (int leftEnd = 0; leftEnd <= i; leftEnd++) {
					int leftCost = leftEnd == -1 ? 0 : dp[leftEnd][j - 1];
					int rightCost = leftEnd == i ? 0 : sum(sum, leftEnd + 1, i);
					int cur = Math.max(leftCost, rightCost);
					if (cur < ans) {
						ans = cur;
					}
				}
				dp[i][j] = ans;
			}
		}
		return dp[N - 1][K];
	}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

我们通过研究依赖关系,发现存在单调性
固定住数组长度情况下,当子数组数量上升,最后得到答案只会下降,当子数组数量下降,最终得到答案只会上升。
子数组变少只会让瓶颈下降,数组长度变长会更麻烦。累加和会变大。反向单调关系。

填表顺序:从左到右,从下到上

	public static int sum(int[] sum, int L, int R) {
		return sum[R + 1] - sum[L];
	}
	public static int splitArray2(int[] nums, int K) {
		int N = nums.length;
		int[] sum = new int[N + 1];
		for (int i = 0; i < N; i++) {
			sum[i + 1] = sum[i] + nums[i];
		}
		int[][] dp = new int[N][K + 1];
		int[][] best = new int[N][K + 1];
		for (int j = 1; j <= K; j++) {
			dp[0][j] = nums[0];
			best[0][j] = -1;
		}
		for (int i = 1; i < N; i++) {
			dp[i][1] = sum(sum, 0, i);
			best[i][1] = -1;
		}
		// 从第2列开始，从左往右
		// 每一列，从下往上
		for (int j = 2; j <= K; j++) {
			for (int i = N - 1; i >= 1; i--) {
				int down = best[i][j - 1];
				// 如果i==N-1，则不优化上限
				int up = i == N - 1 ? N - 1 : best[i + 1][j];
				int ans = Integer.MAX_VALUE;
				int bestChoose = -1;
				for (int leftEnd = down; leftEnd <= up; leftEnd++) {
					int leftCost = leftEnd == -1 ? 0 : dp[leftEnd][j - 1];
					int rightCost = leftEnd == i ? 0 : sum(sum, leftEnd + 1, i);
					int cur = Math.max(leftCost, rightCost);
					if (cur < ans) {
						ans = cur;
						bestChoose = leftEnd;
					}
				}
				dp[i][j] = ans;
				best[i][j] = bestChoose;
			}
		}
		return dp[N - 1][K];
	}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

二分法

我们换一种思路
假定一个目标拆块的时候,拆出来的每一块累加和不能超过这个目标,问你能够做到这一点的情况下,至少要拆几块
当我定好一个X的目标,只要遍历数组一变,我就知道它至少要几个子数组。
先定一个粗略小目标5,当满足这个目标的时候,至少要5块,遍历一遍数组就能搞定
反着求解,先定一个目标,在看我们至少有几块
假设这个问题是f函数搞定的
现在问题是一共就两个子数组,我想知道最合适的目标是什么?
那就从0到所有数字的累加和范围上二分。
二分的时候,你看每个二分点是不是超过两个子数组了
因为目标一定是0~所有数的累加和之间挑,二分的方式总能找到最合适的目标

    public int splitArray(int[] nums, int m) {
        long sum=0;
        int n=nums.length;
        for(int i=0;i<n;i++){
            sum+=nums[i];
        }
        long l=0;
        long r=sum;
        long ans=0;
        while(l<=r){
            long mid=l+(r-l)/2;
            long cur=getNeedPart(nums,mid);
            if(cur<=m){
                ans=mid;
                r=mid-1;
            }else{
                l=mid+1;
            }
        }
        return (int)ans;
    }
    public long getNeedPart(int[] arr,long aim){
        int n=arr.length;
        for(int i=0;i<n;i++){
            if(arr[i]>aim){
                return Integer.MAX_VALUE;
            }
        }
        int all=arr[0];
        int patrs=1;
        for(int i=1;i<n;i++){
            if(all+arr[i]<=aim){
                all+=arr[i];
            }else{
                all=arr[i];
                patrs++;
            }
        }
        return patrs;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40