1. 前言

《MATLAB 神经网络43个案例分析》是MATLAB技术论坛（www.matlabsky.com）策划，由王小川老师主导，2013年北京航空航天大学出版社出版的关于MATLAB为工具的一本MATLAB实例教学书籍，是在《MATLAB神经网络30个案例分析》的基础上修改、补充而成的，秉承着“理论讲解—案例分析—应用扩展”这一特色，帮助读者更加直观、生动地学习神经网络。

《MATLAB神经网络43个案例分析》共有43章，内容涵盖常见的神经网络（BP、RBF、SOM、Hopfield、Elman、LVQ、Kohonen、GRNN、NARX等）以及相关智能算法（SVM、决策树、随机森林、极限学习机等）。同时，部分章节也涉及了常见的优化算法（遗传算法、蚁群算法等）与神经网络的结合问题。此外，《MATLAB神经网络43个案例分析》还介绍了MATLAB R2012b中神经网络工具箱的新增功能与特性，如神经网络并行计算、定制神经网络、神经网络高效编程等。

近年来随着人工智能研究的兴起，神经网络这个相关方向也迎来了又一阵研究热潮，由于其在信号处理领域中的不俗表现，神经网络方法也在不断深入应用到语音和图像方向的各种应用当中，本文结合书中案例，对其进行仿真实现，也算是进行一次重新学习，希望可以温故知新，加强并提升自己对神经网络这一方法在各领域中应用的理解与实践。自己正好在多抓鱼上入手了这本书，下面开始进行仿真示例，主要以介绍各章节中源码应用示例为主，本文主要基于MATLAB2015b(32位)平台仿真实现，这是本书第三十五章粒子群优化算法的寻优算法实例，话不多说，开始！

2. MATLAB 仿真示例

打开MATLAB，点击“主页”，点击“打开”，找到示例文件

选中PSOMutation.m，点击“打开”

PSOMutation.m源码如下：

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%功能：该代码为基于变异粒子群算法的函数极值寻优算法
%环境：Win7，Matlab2015b
%Modi: C.S
%时间：2022-06-21
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%


%% 该代码为基于变异粒子群算法的函数极值寻优算法
%% 清空环境
clc
clear
tic
%% 参数初始化
%粒子群算法中的两个参数
c1 = 1.49445;
c2 = 1.49445;

maxgen=500;   % 进化次数  
sizepop=100;   %种群规模

Vmax=1;
Vmin=-1;
popmax=5;
popmin=-5;

%% 产生初始粒子和速度
for i=1:sizepop
    %随机产生一个种群
    pop(i,:)=5*rands(1,2);    %初始种群
    V(i,:)=rands(1,2);  %初始化速度
    %计算适应度
    fitness(i)=fun(pop(i,:));   %染色体的适应度
end

%% 个体极值和群体极值
[bestfitness bestindex]=min(fitness);
zbest=pop(bestindex,:);   %全局最佳
gbest=pop;    %个体最佳
fitnessgbest=fitness;   %个体最佳适应度值
fitnesszbest=bestfitness;   %全局最佳适应度值

%% 迭代寻优
for i=1:maxgen
    
    for j=1:sizepop
        
        %速度更新
        V(j,:) = V(j,:) + c1*rand*(gbest(j,:) - pop(j,:)) + c2*rand*(zbest - pop(j,:));
        V(j,find(V(j,:)>Vmax))=Vmax;
        V(j,find(V(j,:)<Vmin))=Vmin;
        
        %种群更新
        pop(j,:)=pop(j,:)+0.5*V(j,:);
        pop(j,find(pop(j,:)>popmax))=popmax;
        pop(j,find(pop(j,:)<popmin))=popmin;
        
        if rand>0.98     
            pop(j,:)=rands(1,2);
        end
        
        %适应度值
        fitness(j)=fun(pop(j,:)); 
   
    end
    
    for j=1:sizepop
        
        %个体最优更新
        if fitness(j) < fitnessgbest(j)
            gbest(j,:) = pop(j,:);
            fitnessgbest(j) = fitness(j);
        end
        
        %群体最优更新
        if fitness(j) < fitnesszbest
            zbest = pop(j,:);
            fitnesszbest = fitness(j);
        end
    end 
    yy(i)=fitnesszbest;    
        
end
%% 结果分析
plot(yy)
title('最优个体适应度','fontsize',12);
xlabel('进化代数','fontsize',12);ylabel('适应度','fontsize',12);
% web browser www.matlabsky.com
toc
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89

调用函数源码如下：

function y = fun(x)
%函数用于计算粒子适应度值
%x           input           输入粒子 
%y           output          粒子适应度值 

y=-20*exp(-0.2*sqrt((x(1)^2+x(2)^2)/2))-exp((cos(2*pi*x(1))+cos(2*pi*x(2)))/2)+20+exp(1);

%y=x(1)^2-10*cos(2*pi*x(1))+10+x(2)^2-10*cos(2*pi*x(2))+10;
1
2
3
4
5
6
7
8

添加完毕，点击“运行”，开始仿真，输出仿真结果如下：

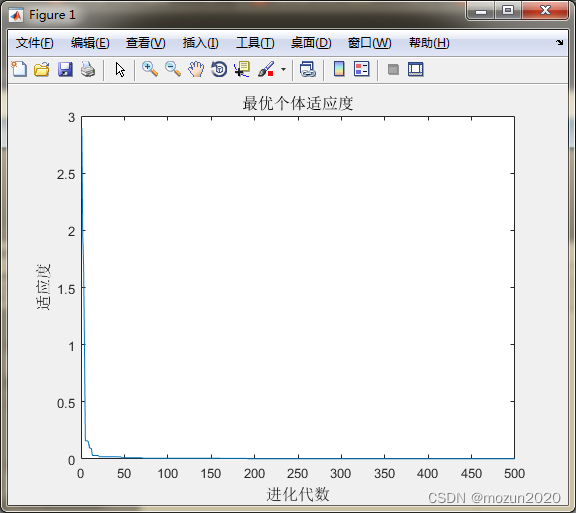
3. 小结

粒子群优化算法(Particle Swarm optimization,PSO)又翻译为粒子群算法、微粒群算法、或微粒群优化算法。是通过模拟鸟群觅食行为而发展起来的一种基于群体协作的随机搜索算法。通常认为它是群集智能 (Swarm intelligence, SI) 的一种。它可以被纳入多主体优化系统(Multiagent Optimization System, MAOS)。粒子群优化算法是由Eberhart博士和kennedy博士提出。对本章内容感兴趣或者想充分学习了解的，建议去研习书中第三十五章节的内容。后期会对其中一些知识点在自己理解的基础上进行补充，欢迎大家一起学习交流。