• 暑假算法训练day3

    目录

    C. Challenging Cliffs

    题意：
    在这里插入图片描述
    思路：把高度差最小的放两边。分别将比 a 1 a_1 a1​大的按递增放 a 1 a_1 a1​后边，将比 a n a_n an​大的按递增放 a n a_n an​前边

    #include <bits/stdc++.h>
using namespace std;
const double pi = acos(-1.0);
#define x first
#define y second
#define LL long long 
#define int LL
#define pb push_back
#define all(v) (v).begin(),(v).end()
#define PII pair<int,int>
#define ll_INF 0x7f7f7f7f7f7f7f7f
#define INF 0x3f3f3f3f
#define debug(x) cerr << #x << ": " << x << endl
#define io ios_base::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr)
LL Mod(LL a,LL mod){return (a%mod+mod)%mod;}
LL lowbit(LL x){return x&-x;}//最低位1及其后面的0构成的数值
LL qmi(LL a,LL b,LL mod) {LL ans = 1; while(b){ if(b & 1) ans = ans * (a % mod) % mod; a = a % mod * (a % mod) % mod; b >>= 1;} return ans; }
int _;
int n;
const int N=2e5+10;
int a[N];
void solve()
{
	cin>>n;
	for(int i=1;i<=n;i++)cin>>a[i];
	int d=ll_INF;
	int x=0,y=0;
	int idx1=0,idx2=0;
	sort(a+1,a+1+n);
	for(int i=2;i<=n;i++)
	{
		if(d>abs(a[i]-a[i-1]))
		{
			x=a[i],y=a[i-1];
			idx1=i-1,idx2=i;
			d=abs(a[i]-a[i-1]);
		}
	}
	if(x>y)swap(x,y);
	vector<int>v1,v2;
	for(int i=1;i<=n;i++)
	{
		if(i==idx1||i==idx2)continue;
		if(a[i]>=x)v1.pb(a[i]);
		else v2.pb(a[i]);
	}
	cout<<x<<' ';
	for(auto x:v1)cout<<x<<' ';
	for(auto x:v2)cout<<x<<' ';
	cout<<y<<endl;
}
signed main()
{
    io;
 	cin>>_; 
 	while(_--)
    solve();
    return 0;
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38
    • 39
    • 40
    • 41
    • 42
    • 43
    • 44
    • 45
    • 46
    • 47
    • 48
    • 49
    • 50
    • 51
    • 52
    • 53
    • 54
    • 55
    • 56
    • 57
    • 58
    • 59

    B. Prinzessin der Verurteilung

    题意：
    在这里插入图片描述
    思路：
    字符串长度不超过1000，而 2 6 3 > 1000 26^3>1000 263>1000证明满足题意得子串长度最大为3

    #include <bits/stdc++.h>
using namespace std;
const double pi = acos(-1.0);
#define x first
#define y second
#define LL long long 
#define int LL
#define pb push_back
#define all(v) (v).begin(),(v).end()
#define PII pair<int,int>
#define ll_INF 0x7f7f7f7f7f7f7f7f
#define INF 0x3f3f3f3f
#define debug(x) cerr << #x << ": " << x << endl
#define io ios_base::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr)
LL Mod(LL a,LL mod){return (a%mod+mod)%mod;}
LL lowbit(LL x){return x&-x;}//最低位1及其后面的0构成的数值
LL qmi(LL a,LL b,LL mod) {LL ans = 1; while(b){ if(b & 1) ans = ans * (a % mod) % mod; a = a % mod * (a % mod) % mod; b >>= 1;} return ans; }
int _;
int n;
void solve()
{
	cin>>n;
	string s;
	cin>>s;
	string a="";
	queue<pair<string,int>>q;
	q.push({a,0});
	while(q.size())
	{
		auto t=q.front();
		q.pop();
		t.x.resize(t.y+1);
		for(char c='a';c<='z';c++)
		{
			t.x[t.y]=c;
			if(s.find(t.x)==-1)
			{
				cout<<t.x<<endl;
				return;
			}
			else q.push({t.x,t.y+1});
		}
	}
}
signed main()
{
    io;
 	cin>>_; 
 	while(_--)
    solve();
    return 0;
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38
    • 39
    • 40
    • 41
    • 42
    • 43
    • 44
    • 45
    • 46
    • 47
    • 48
    • 49
    • 50
    • 51
    • 52

    B1. Palindrome Game (easy version)

    题意：
    在这里插入图片描述
    思路：
    A和B足够聪明，所以A和B要尽可能在自己操作完一次后形成一个回文串。
    如果零得个数为偶数只有两种情况：

    1. 平手
    2. B获胜

    但是A的操作对答案无影响，所以B足够聪明，B就一定能获胜（后出手）。
    如果零的个数是奇数：
    A第一次放在最中间，那么剩下偶数个是B起手，那么

    1. A赢
      在这里插入图片描述

    2. B赢（只要A在第三步反转“作死”，B赢，但是两个人足够聪明，所以排除这种情况）
      在这里插入图片描述

      综上所述，如果零的个数为偶数或者1，Bwin，如果是奇数，Awin

    #include <bits/stdc++.h>
using namespace std;
const double pi = acos(-1.0);
#define x first
#define y second
#define LL long long 
#define int LL
#define pb push_back
#define all(v) (v).begin(),(v).end()
#define PII pair<int,int>
#define ll_INF 0x7f7f7f7f7f7f7f7f
#define INF 0x3f3f3f3f
#define debug(x) cerr << #x << ": " << x << endl
#define io ios_base::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr)
LL Mod(LL a,LL mod){return (a%mod+mod)%mod;}
LL lowbit(LL x){return x&-x;}//最低位1及其后面的0构成的数值
LL qmi(LL a,LL b,LL mod) {LL ans = 1; while(b){ if(b & 1) ans = ans * (a % mod) % mod; a = a % mod * (a % mod) % mod; b >>= 1;} return ans; }
int _;
int n;
void solve()
{
	cin>>n;
	string s;
	cin>>s;
	int one=0,zero=0;
	for(int i=0;i<n;i++) 
		if(s[i]=='0')zero++;
		else one++;
	if(zero==0)
	{
		cout<<"DRAW"<<endl;
		return;
	}
	else if(zero%2)
	{
		if(zero>1)cout<<"ALICE"<<endl;
		else cout<<"BOB"<<endl;
	    return;
	}
	else
	{
	    cout<<"BOB"<<endl;
	    return;
	}
}
signed main()
{
    io;
 	cin>>_; 
 	while(_--)
    solve();
    return 0;
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38
    • 39
    • 40
    • 41
    • 42
    • 43
    • 44
    • 45
    • 46
    • 47
    • 48
    • 49
    • 50
    • 51
    • 52
    • 53

    C. Factorials and Powers of Two

    题意：
    在这里插入图片描述
    思路：
    d ! d! d!当 d = 15 d=15 d=15时已经超过题目给的范围，我们发现， 2 d 2^d 2d是2进制中1的个数，如果k要求最小，那么 2 d 2^d 2d的个数尽可能少， d ! d! d!尽可能大，考虑状态压缩，枚举剪掉的 d ! d! d!。

    #include <bits/stdc++.h>
using namespace std;
const double pi = acos(-1.0);
#define x first
#define y second
#define LL long long 
#define int LL
#define pb push_back
#define all(v) (v).begin(),(v).end()
#define PII pair<int,int>
#define ll_INF 0x7f7f7f7f7f7f7f7f
#define INF 0x3f3f3f3f
#define debug(x) cerr << #x << ": " << x << endl
#define io ios_base::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr)
LL Mod(LL a,LL mod){return (a%mod+mod)%mod;}
LL lowbit(LL x){return x&-x;}//最低位1及其后面的0构成的数值
LL qmi(LL a,LL b,LL mod) {LL ans = 1; while(b){ if(b & 1) ans = ans * (a % mod) % mod; a = a % mod * (a % mod) % mod; b >>= 1;} return ans; }
int _;
int n;
const int N=21;
int f[N];
int cnt(int x)
{
	int res=0;
	while(x)
	{
		if(x&1)res++;
		x>>=1;
	}
	return res;
}
void solve()
{ 
	int x;
	cin>>x;
	int res=cnt(x);
	for(int i=0;i<1<<15;i++)
	{
		int y=x;
		for(int j=0;j<15;j++)
		{
			if((i>>j)&1)y-=f[j+1];
		}
		if(y>=0)res=min(res,cnt(y)+cnt(i));
	}
	cout<<res<<endl;
}
signed main()
{
    io;
    f[0]=1;
    for(int i=1;i<=15;i++)f[i]=f[i-1]*i;
 	cin>>_; 
 	while(_--)
    solve();
    return 0;
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38
    • 39
    • 40
    • 41
    • 42
    • 43
    • 44
    • 45
    • 46
    • 47
    • 48
    • 49
    • 50
    • 51
    • 52
    • 53
    • 54
    • 55
    • 56
    • 57

    C. Not Assigning

    题意：
    在这里插入图片描述
    思路：
    素数除了2以外都是奇数，奇数+奇数=偶数，偶数+奇数=奇数
    可知这棵树一定是一条链，一种方案是轮换放2，3
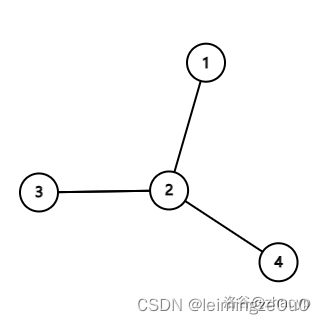
    在这里插入图片描述

    #include <bits/stdc++.h>
using namespace std;
const double pi = acos(-1.0);
#define x first
#define y second
#define LL long long 
#define int LL
#define pb push_back
#define all(v) (v).begin(),(v).end()
#define PII pair<int,int>
#define ll_INF 0x7f7f7f7f7f7f7f7f
#define INF 0x3f3f3f3f
#define debug(x) cerr << #x << ": " << x << endl
#define io ios_base::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr)
LL Mod(LL a,LL mod){return (a%mod+mod)%mod;}
LL lowbit(LL x){return x&-x;}//最低位1及其后面的0构成的数值
LL qmi(LL a,LL b,LL mod) {LL ans = 1; while(b){ if(b & 1) ans = ans * (a % mod) % mod; a = a % mod * (a % mod) % mod; b >>= 1;} return ans; }
int _;
int n;
const int N=1e5+10;
int h[N],e[N*2],ne[N*2],idx;
int d[N];
map<PII,int>mp;
PII q[N];
void add(int a,int b)
{
	e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
void dfs(int u,int fa,int f)
{
	if(h[u]==-1)return;
	for(int i=h[u];~i;i=ne[i])
	{
		int j=e[i];
		if(j==fa)continue;
		if(f)mp[{u,j}]=mp[{j,u}]=2;
		else mp[{u,j}]=mp[{j,u}]=3;
		f^=1;
		dfs(j,u,f);
	}
}
void solve()
{ 
	cin>>n;
	idx=0;
	memset(h,-1,sizeof h);
	for(int i=1;i<=n;i++)d[i]=0;
	for(int i=0;i<n-1;i++)
	{
		int a,b;
		cin>>a>>b;
		add(a,b),add(b,a);
		d[a]++,d[b]++;
		q[i]={a,b};
	}
	int root=-1;
	for(int i=1;i<=n;i++)
	{
		if(d[i]>2)
		{
			cout<<-1<<endl;
			return;
		}
		if(d[i]==1)
		{
			root=i;
		}
	}
	dfs(root,-1,0);
	for(int i=0;i<n-1;i++)
	{
		cout<<mp[q[i]]<<' ';
	}
	cout<<endl; 
}
signed main()
{
    io;
 	cin>>_; 
 	while(_--)
    solve();
    return 0;
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38
    • 39
    • 40
    • 41
    • 42
    • 43
    • 44
    • 45
    • 46
    • 47
    • 48
    • 49
    • 50
    • 51
    • 52
    • 53
    • 54
    • 55
    • 56
    • 57
    • 58
    • 59
    • 60
    • 61
    • 62
    • 63
    • 64
    • 65
    • 66
    • 67
    • 68
    • 69
    • 70
    • 71
    • 72
    • 73
    • 74
    • 75
    • 76
    • 77
    • 78
    • 79
    • 80
    • 81
    • 82
    • 83

    D. Weights Assignment For Tree Edges

    题意：
    在这里插入图片描述
    思路：
    我们可以构造两个点之间的距离是他们距离根节点的差值，dfs即可

    #include <bits/stdc++.h>
using namespace std;
const double pi = acos(-1.0);
#define x first
#define y second
#define LL long long 
#define int LL
#define pb push_back
#define all(v) (v).begin(),(v).end()
#define PII pair<int,int>
#define ll_INF 0x7f7f7f7f7f7f7f7f
#define INF 0x3f3f3f3f
#define debug(x) cerr << #x << ": " << x << endl
#define io ios_base::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr)
LL Mod(LL a,LL mod){return (a%mod+mod)%mod;}
LL lowbit(LL x){return x&-x;}//最低位1及其后面的0构成的数值
LL qmi(LL a,LL b,LL mod) {LL ans = 1; while(b){ if(b & 1) ans = ans * (a % mod) % mod; a = a % mod * (a % mod) % mod; b >>= 1;} return ans; }
int _;
int n;
const int N=2e5+10;
int h[N],ne[N<<1],e[N<<1],idx=1;
int d[N];
int c[N];
void add(int a,int b)
{
	e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
void dfs(int u)
{
	for(int i=h[u];~i;i=ne[i])
	{
		int j=e[i];
		if(j==u)continue;
		d[i]=c[j]-c[u];
		dfs(j);	
	}
}
void solve()
{ 
	cin>>n;
	idx=1;
	int root=-1;
	memset(h,-1,sizeof h);
	for(int i=1;i<=n;i++)
	{
		int x;
		cin>>x;
		if(x==i)
		{
			root=x;
			d[root]=0;
		}
		add(x,i);
	}
	for(int i=1;i<=n;i++)
	{
		int x;
		cin>>x;
		c[x]=i;
	}
	dfs(root);
	for(int i=1;i<=n;i++)
	{
		if(d[i]<0)
		{
			cout<<-1<<endl;
			return;
		}
	}
	for(int i=1;i<=n;i++)cout<<d[i]<<' ';
	cout<<endl;
}
signed main()
{
    io;
 	cin>>_; 
 	while(_--)
    solve();
    return 0;
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38
    • 39
    • 40
    • 41
    • 42
    • 43
    • 44
    • 45
    • 46
    • 47
    • 48
    • 49
    • 50
    • 51
    • 52
    • 53
    • 54
    • 55
    • 56
    • 57
    • 58
    • 59
    • 60
    • 61
    • 62
    • 63
    • 64
    • 65
    • 66
    • 67
    • 68
    • 69
    • 70
    • 71
    • 72
    • 73
    • 74
    • 75
    • 76
    • 77
    • 78
    • 79
    • 80
  • 相关阅读:
    豪华低价不是国产新能源的“良药”
    LeetCode【2251. 花期内花的数目】
    跨平台宏定义
    1.4+1.5 L1、L2正则化
    GJB 128B-2021标准版本变更汇总 ,发布， 下载
    数据库中的DDL与DML
    新服务入驻生产环境 CICD 全流程、自动化脚本教程
    航天环宇提交招股书上会稿：计划募资6亿元，控股股东为李完小
    使用Hot Chocolate和.NET 6构建GraphQL应用(9) —— 实现Mutate更新数据
    C++图像金字塔下采样的函数
  • 原文地址：https://blog.csdn.net/qq_52765554/article/details/125465920