一、理论基础

1、算术优化算法

请参考这里。

2、IX-AOA原理介绍

（1）微调更新时间分配

为更好的分配算法寻优时间，采用非线性曲线调整算法不同时间勘探和开发的功能切换，其数学模型如下式：$$f=5+10\times rand(1,1)\text{\hspace{1em}(1)}$$$$MOA=t-(2+\text{csch}(1+\log (t/T)){)}^f\text{\hspace{1em}(2)}$$其中，$\log$表示以$e$为底的对数，$f$定义为区间$[5,15]$之间的随机整数，保证了算法在前后期勘探与开发并存，分工合作达到更好的寻优效果，同时由式(2)可知，根据双曲线性质，$\text{csch}(t)$仍为递减函数且双曲线减缓了曲线下降速度，且前期函数值取值较小采用算法全局搜索功能大范围遍历候选解进行最优值更新；同时算法后期随着迭代次数增加函数值增加，随机值大于 MOA的情况下进行全局勘探，围绕最优个体进行局部极值识别更新最优解，达到收敛精度的提升效果。

（2）最优个体激活引导策略

标准AOA中并没有充分利用最优个体位置的信息，因此提出一种基于sigmoid激活函数的最优个体引导位置更新方程，即：$$w=M\_max-(M\_max-M\_min)/(1+\exp (1-\tau \times t/T))\text{\hspace{1em}(3)}$$借鉴粒子群(PSO)中利用惯性权重调整勘探和开发的启发，在AOA位置更新部分使用较大的权重有利于全局搜索，较小的权重将优化局部开发，在此，惯性权重使用基于sigmoid激活函数曲线特性微调算法功能，经过多次试验节可得$\mu$为20其寻优效果最佳，其调节曲线sigmoid函数曲线如下图1所示。

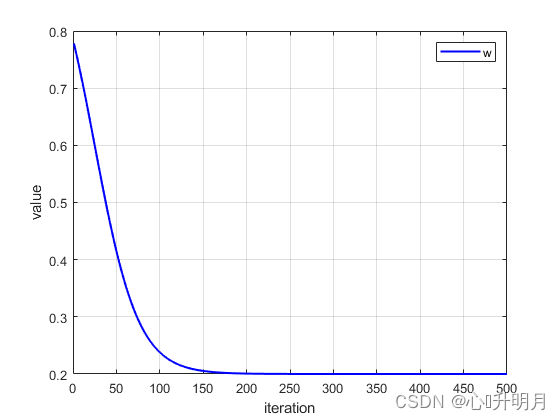
图1 $w$函数曲线

图1绘制了sigmoid曲线后半部分曲线，从图中看出，迭代初期较大的$w$值有益于算法早期的全局搜索能力优化，后期较小的$w$值改善算法后期的局部开发功能，使得算法整体性能得到有效协调。

（3）小孔成像学习策略

小孔成像原理请参考这里。由于小孔成像产生的候选解不排除解覆盖现象，种群多样性并没有得到改善，由此，在小孔成像位置更新部分加入双曲线，增加候选解错开分布性，达到改善种群分布的目标。$$delta=(t-1)/T\text{\hspace{1em}(4)}$$$$u=(-t{)}^{\ast }\text{csch}(delt{a}^{\ast }t{)}^2\text{\hspace{1em}(5)}$$$$x^{\prime \ast }=u^{\ast }((a+b)/2+(a+b)/(2^{\ast }k))-x_{i,j}/k)\text{\hspace{1em}(6)}$$其中，当前迭代次数$t$从2初始迭代，$x^{\prime \ast }$与$x_{i,j}$分别表示新机制更新位置以及当前第$i$个解的第$j$个位置。

（4）IX-AOA执行流程

IX-AOA迭代寻优进程主要步骤如下：
Step 1：初始化算法参数，如$Alpha$、$\mu$等。
Step 2：初始种群位置，并确定初始最优个体和最优值。
Step 3：根据基本AOA对应公式计算MOP和式(2)计算MOA确定算法寻优机制，根据MOA随着迭代次数变化纵向微调算法寻优过程。
Step 4：种群个体横向更新，按照式(3)随迭代次数$t$动态更新权重系数，横向更新种群个体进化产生子代种群个体。
Step 5：当前位置的多样性候选解生成。当算法进行到后期时，在当前位置的范围内即$[a,b]$按照式(6)产生交错分布的候选解，对当前位置周围进行二次开采以丰富算法种群多样性。
Step 6：对候选解之间适应度进行竞争对比，保留更有价值的位置信息。
Step 7：判断当前迭代步数是否达到最大迭代次数，若是，则算法终止进程并输出最优值以及最佳个体解信息；否则返回Step 3。

二、仿真实验与结果分析

将IX-AOA与AOA、GWO和SSA进行对比，以常用23个测试函数中的F3、F4(单峰函数/100维)、F10、F11(多峰函数/100维)、F19、F20(固定维度多峰函数/3维、6维)为例，实验设置种群规模为30，最大迭代次数为500，每种算法独立运算30次，结果显示如下：

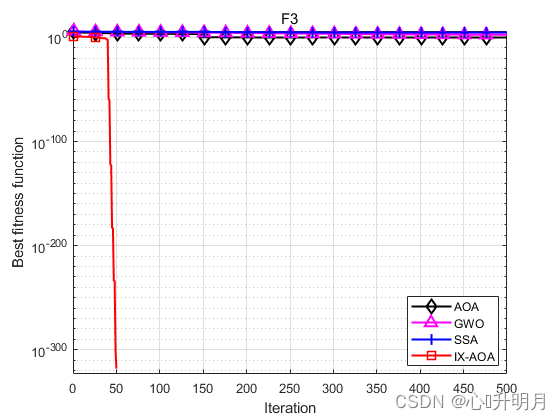
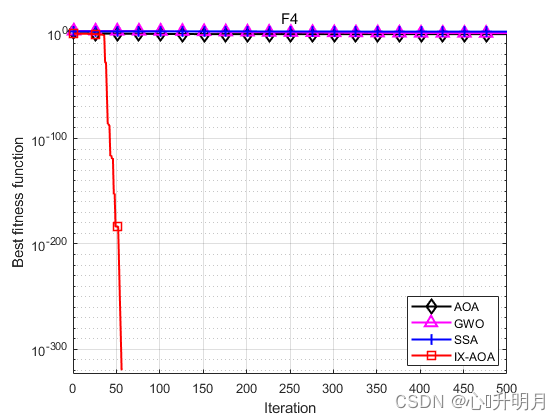
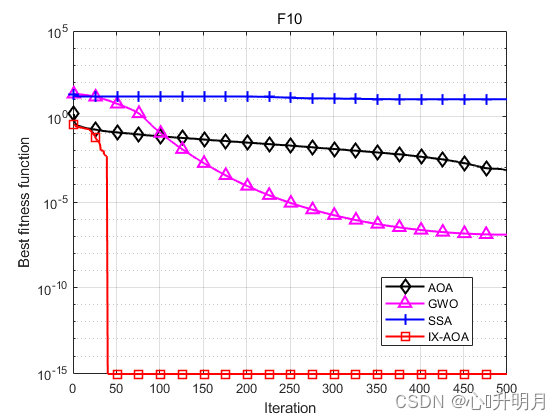
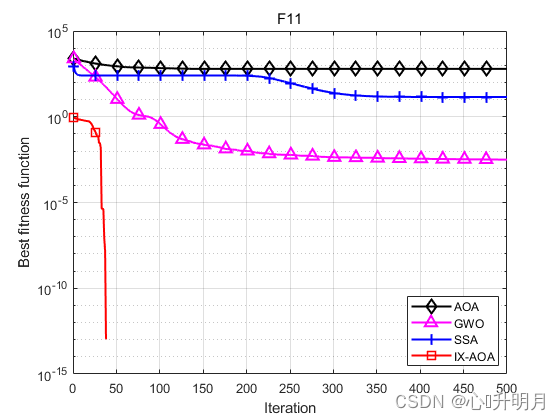
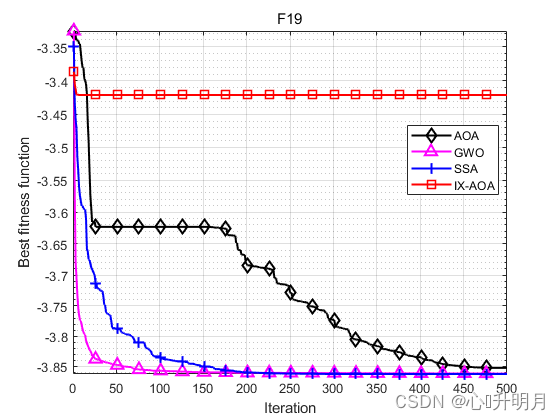
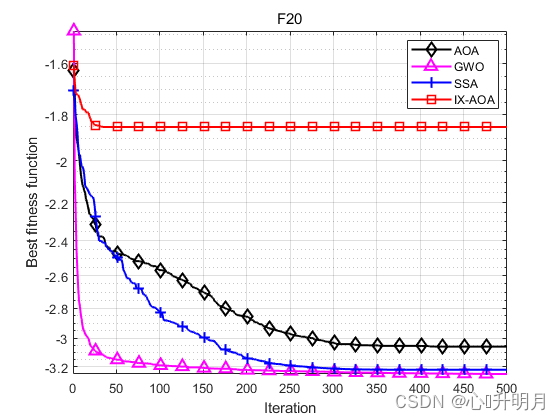
函数：F3
AOA：Best: 0.29967,Worst: 3.8522,Mean: 0.83113,Sstd: 0.80228
GWO：Best: 18.1232,Worst: 1600.5964,Mean: 333.3045,Std: 329.8962
SSA：Best: 16949.2831,Worst: 95733.9141,Mean: 49757.2582,Std: 22148.3184
IXAOA：Best: 0,Worst: 0,Mean: 0,Std: 0
函数：F4
AOA：Best: 0.071581,Worst: 0.14109,Mean: 0.094635,Sstd: 0.012826
GWO：Best: 0.042698,Worst: 5.0382,Mean: 0.82891,Std: 1.032
SSA：Best: 22.6646,Worst: 32.5421,Mean: 27.6167,Std: 2.6499
IXAOA：Best: 0,Worst: 0,Mean: 0,Std: 0
函数：F10
AOA：Best: 8.8818e-16,Worst: 0.0033038,Mean: 0.00074075,Sstd: 0.0011248
GWO：Best: 5.6446e-08,Worst: 2.3807e-07,Mean: 1.2391e-07,Std: 5.0681e-08
SSA：Best: 8.3456,Worst: 13.1789,Mean: 10.1938,Std: 1.3365
IXAOA：Best: 8.8818e-16,Worst: 8.8818e-16,Mean: 8.8818e-16,Std: 0
函数：F11
AOA：Best: 218.9727,Worst: 991.8197,Mean: 620.6591,Sstd: 187.6163
GWO：Best: 8.5265e-14,Worst: 0.03237,Mean: 0.0031719,Std: 0.0086384
SSA：Best: 6.759,Worst: 22.0775,Mean: 14.1508,Std: 3.9413
IXAOA：Best: 0,Worst: 0,Mean: 0,Std: 0
函数：F19
AOA：Best: -3.8624,Worst: -3.8422,Mean: -3.8526,Sstd: 0.0044611
GWO：Best: -3.8628,Worst: -3.8549,Mean: -3.8621,Std: 0.0017835
SSA：Best: -3.8628,Worst: -3.8628,Mean: -3.8628,Std: 1.011e-11
IXAOA：Best: -3.7955,Worst: -2.6157,Mean: -3.421,Std: 0.28633
函数：F20
AOA：Best: -3.1736,Worst: -2.828,Mean: -3.0579,Sstd: 0.083611
GWO：Best: -3.322,Worst: -3.0842,Mean: -3.2551,Std: 0.076845
SSA：Best: -3.322,Worst: -3.1592,Mean: -3.2238,Std: 0.061175
IXAOA：Best: -2.7606,Worst: -1.069,Mean: -1.8512,Std: 0.38402
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

实验结果表明：IX-AOA有效提高了算法寻优效率，显示了其早期强势的全局搜索以及良好的局部极值识别精确度。

三、参考文献

[1] 杨文珍, 何庆. 融合微平衡激活的小孔成像算术优化算法[J/OL]. 计算机工程与应用: 1-11 [2022-06-21].