LeetCode高频题42. 接雨水

提示：本题是系列LeetCode的150道高频题，你未来遇到的互联网大厂的笔试和面试考题，基本都是从这上面改编而来的题目
互联网大厂们在公司养了一大批ACM竞赛的大佬们，吃完饭就是设计考题，然后去考应聘人员，你要做的就是学基础树结构与算法，然后打通任督二脉，以应对波云诡谲的大厂笔试面试题！
你要是不扎实学习数据结构与算法，好好动手手撕代码，锻炼解题能力，你可能会在笔试面试过程中，连题目都看不懂！比如华为，字节啥的，足够让你读不懂题

基础知识：
【1】LeetCode高频题11：盛最多水的容器

---

文章目录

• LeetCode高频题42. 接雨水
• • @[TOC](文章目录)
• 题目
• 一、审题
• 耗费额外空间，找最大值预设数组
• 优化空间o(1)，面试最优解，用maxL和maxR表示i左侧最大值，和右侧最大值，取小的话，结算就结算瓶颈这边的水量
• 总结

题目

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

---

一、审题

示例 1：

输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。
示例 2：

输入：height = [4,2,0,3,2,5]
输出：9

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/trapping-rain-water
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

---

耗费额外空间，找最大值预设数组

先从左往右，找0–i-1上最大值maxL，记录为一个left数组
再从右往左，找i+1–N-1上最大值maxR，记录为一个right数组
每次来到i位置，看看left[i]和right[i]最小值就是瓶颈，减掉[i]就是水量，累加和就是结果

手撕代码：

        //复习：2
        public int trapReview2(int[] height) {
            if (height == null || height.length < 3) return 0;//至少要3根板子，2根不行
            //maxL=[0]和maxR=[N-1]从两边记录最大值
            int N = height.length;
            int[] left = new int[N];
            int[] right = new int[N];
            //先从左往右，找0--i-1上最大值maxL，记录为一个left数组
            left[0] = height[0];
            for (int i = 1; i < N; i++) {
                left[i] = height[i] > left[i - 1] ? height[i] : left[i - 1];//[i]大换，否则还是左边大
            }
            //再从右往左，找i+1--N-1上最大值maxR，记录为一个right数组
            right[N - 1] = height[N - 1];
            for (int i = N - 2; i >= 0; i--) {
                right[i] = height[i] > right[i + 1] ? height[i] : right[i + 1];//[i]大换，否这右边大
            }
            //每次来到i位置，看看left[i]和right[i]最小值就是瓶颈，减掉[i]就是水量，累加和就是结果
            int ans = 0;
            for (int i = 1; i < N - 1; i++) {
                //结算i
                ans += Math.max(0, Math.min(left[i - 1], right[i + 1]) - height[i]);
                //如果i太高没水
            }

            return ans;
        }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

测试：

    public static void test(){
        int[] arr = {4,2,0,3,2,5};
        Solution solution = new Solution();
        System.out.println(solution.trap(arr));
        System.out.println(solution.trapReview(arr));
        System.out.println(solution.trapReview2(arr));
    }


    public static void main(String[] args) {
        test();
    }
1
2
3
4
5
6
7
8
9
10
11
12

9
9
9
1
2
3

问题不大，LeetCode测试：


速度其实慢了点，而且left和right还耗费了额外空间

观察一下，不就是要左边最大值，右边最小值，两者取小结算吗
能否省下left和right数组，用maxL和maxR表示呢？？？

完全可以！

---

优化空间o(1)，面试最优解，用maxL和maxR表示i左侧最大值，和右侧最大值，取小的话，结算就结算瓶颈这边的水量

本题和基础知识：
【1】LeetCode高频题11：盛最多水的容器
这个题目，方法基本一样，题目微微有区别，那个题目就是让你组合最大的水桶，
以底边a为最长，考虑桶越高就接越多水

本题就是让你整体看看每个位置能借多少水，求和加起来就是总量【有点区别，可以仔细体会一下，方法类似】

这题，就是接雨水，看水桶i位置左右的桶高瓶颈
i位置上方能留下几个水？？？

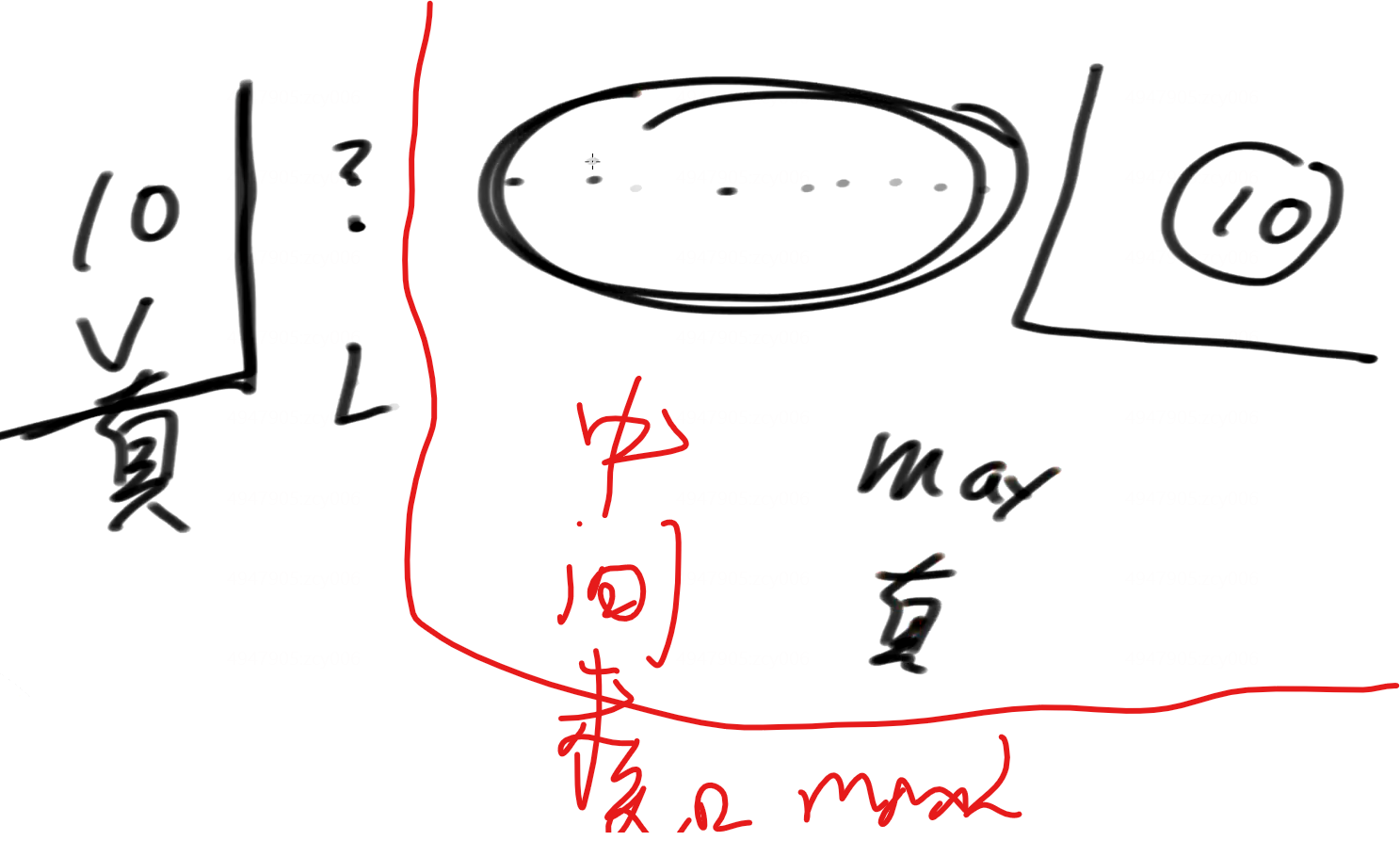
i位置高度为5，它左边最高高度能到10
右边最高高度能到20
则瓶颈就是左边的10
再加水就要从左边溜出去

故，i=5处能接水高度是10-5

来到i，记忆左侧的最大值，右边最大值
瓶颈-我i处的高，就是i能接的水
当然i太高，接0格水
边界0和N-1位置无法接水

为啥不关注中间更高的呢？没用，因为我要看两边最高的，看的是瓶颈

所以方法很简单：
maxL=[0]和maxR=[N-1]从两边记录最大值
L从1开始，R从N-2开始，看看maxL和maxR的关系
（1）maxL<maxR,先结算L处【因为L瓶颈，L左边不会再有比我更高的桶，所以先结算左边】，L++
（2）maxL>maxR,先结算R处【因为R瓶颈，R右边不会再有比我更高的桶，所以先结算右边】，R–
（3）maxL=maxR，同时结算L与R处，L++，R–
中途不要忘记更新maxL和maxR

每个位置结算公式：

maxL和maxR谁小谁是瓶颈，先结算这边，用min-[i]就是水量
但是如果[i]太高大于min，则水量是负数，没法接水，就取0水量
上面红色那个

maxL和maxR谁小谁先结算，为啥呢？

左边小，那中间可能还有更高的高度也没关系，因为瓶颈是左边的最大值
同理右边小右边结算右边

再换个思路理解
其实，为啥昨天小，先结算L，因为左边真的所有最大都出来了，L右边那些有个最大是10，但是中间那些不知道啊，不过没关系，右边就是比左边小，瓶颈也是右边maxR，要是中间比我maxL还小，没关系啊，瓶颈是左边maxL
所以先结算真的maxL这边呗，
同理，右边是瓶颈就结算真的右边maxR，左边中间的不管

最后把结果加起来给ans

手撕代码非常简单

        //复习：
        public int trapReview(int[] height) {
            if (height == null || height.length < 3) return 0;//至少要3根板子，2根不行
            //maxL=[0]和maxR=[N-1]从两边记录最大值
            int N = height.length;
            int maxL = height[0];
            int maxR = height[N - 1];
            //L从1开始，R从N-2开始，看看maxL和maxR的关系
            int L = 1;
            int R = N - 2;
            int ans = 0;//水量结果
            while (L <= R){
                //当L=R时最后一个结算
                //（1）maxL<maxR,先结算L处，L++
                if (maxL < maxR) {
                    ans += Math.max(0, maxL - height[L]);
                    maxL = Math.max(height[L++], maxL);//更新L和maxL
                }
                //（2）maxL>maxR,先结算R处，R--
                else {
                    ans += Math.max(0, maxR - height[R]);
                    maxR = Math.max(height[R--], maxR);//更新R和maxR
                }
                //（3）maxL=maxR，同时结算L与R处，L++，R--，也可以只移动一个，保证L=R时只算一次
                //(2)(3)融合了，所以把，都行
            }

            return ans;
        }
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

测试：

public static void test(){
        int[] arr = {4,2,0,3,2,5};
        Solution solution = new Solution();
        System.out.println(solution.trap(arr));
        System.out.println(solution.trapReview(arr));
    }


    public static void main(String[] args) {
        test();
    }
1
2
3
4
5
6
7
8
9
10
11

9
9
1
2

LeetCode测试：


老牛了吧！
L++，R–，相遇结束，就是o(n）复杂度
这速度比上面预设数组快，空间也更好

---

总结

提示：重要经验：

1）本题跟之前盛水最多的容器颇有相似之处，盛水主要是找底边最大情况下，尽量拿最高的桶，看maxL和maxR谁是瓶颈
2）本题也是来到L,R位置，看看左边大，还是右边大，看看瓶颈，结算水量，然后更新maxL和maxR，o(n)搞定
3）笔试求AC，可以不考虑空间复杂度，但是面试既要考虑时间复杂度最优，也要考虑空间复杂度最优。