目录

1. 概要

2. Simulink求解器

2.1 Simulink仿真过程

2.2 Simulink求解器分类

2.3 Simulink仿真参数设置界面

3. 定步长求解器 fixed step discrete solver

3.1 定步长离散求解器 fixed step discrete solver

3.2 定步长连续求解器 fixed step continuous solver

3.2.1 显式定步长连续求解器

3.2.2 隐式定步长连续求解器

4. Choose a Fixed-Step Solver

4.1 When to Use a Fixed-Step Solver

​​​​​​​4.2 选择定步长的基本流程

5. 变步长求解器

​​​​​​​5.1 变步长离散求解器

​​​​​​​5.2 变步长连续求解器

​​​​​​​5.2.1 显式变步长连续求解器

5.2.2 隐式变步长连续求解器

5.3 ​​​​​​​变步长求解器的误差容限（Error Tolerances）

5.3.1 局部误差 Local Error

​​​​​​​5.3.2 绝对误差容限Absolute Tolerances

5.3.3 小贴士

6. 一个简单例子：求解器选择对仿真结果的影响

---

 

1. 概要

        本文综合性地介绍Simulink求解器的方方面面。最后通过一个简单的例子示例了求解器的配置选择对于仿真结果的影响。

2. Simulink求解器

2.1 Simulink仿真过程

Simulink 模型的执行分几个阶段进行。首先进行的是初始化阶段，在此阶段，Simulink 将库模型块合并到模型中来，确定传送宽度、数据类型和采样时间，计算块参数，确定块的执行顺序，以及分配内存。然后，Simulink 进入到“仿真循环”，每次循环仿真时间前进一个仿真“时间步”， 时间步（time step）是发生计算的时间间隔, 此时间间隔的大小称为步长。在每个仿真时间步期间，Simulink 按照初始化阶段确定的块执行顺序依次执行模型中的每个块。对于每个块而言，Simulink 调用函数来计算块在当前采样时间下的状态，导数和输出。如此反复，一直持续到仿真结束。以这种方式计算模型状态的过程称为解算模型。

 

2.2 Simulink求解器分类

 

没有任何一种模型解算方法能适用于所有系统。Simulink® 提供了一组程序，称为求解器。每个求解器代表一种特定的模型解算方法。

求解器运用一种数值方法来解算代表模型的一组常微分方程。通过这种计算，它确定下一个仿真步的时间。在解算此初始值问题的过程中，求解器还满足您指定的准确性要求。

数学家们开发出了多种数值积分方法来解算表示动态系统连续状态的常微分方程 (ODE)。提供了一套全面的定步长和变步长连续求解器，其中每个求解器实现一种特定的 ODE 解法（请参阅比较求解器）。在模型配置参数的求解器窗格中选择求解器。

MATLAB® 和 Simulink 提供的所有求解器都遵循类似的命名约定：ode 后跟两三个数字（表示求解器的阶）。有些求解器可以求解刚性微分方程，它们使用的方法由 s、t 或 tb 后缀表示。

 

Simulink求解器基于计算步长类型分类可分为两大类：变步长求解器和定步长求解器。基于模型状态分类可分为：连续与离散求解器。还进一步细分为：隐式求解与显式求解、单步求解与多步求解以及单阶式与变阶式求解。

（1）定步长与变步长求解器

定步长求解器的仿真步长固定，没有误差控制机制；变步长求解器在仿真过程中需要计算仿真步长，通过增加/减小步长来满足所设定的误差宽容限。在生成实时运算代码时，必须使用定步长求解器，若不打算配置模型代码生成，求解器的选择根据模型的特性及仿真速度、精确度等要求而定。通常，变步长求解器可以减少仿真时间，定步长求解步长越小，仿真精度越高，故在同样仿真精度要求下，在采用定步长求解器进行仿真时，整个仿真过程必须采用变步长求解器中的最小步长。

（2）连续与离散求解器

在定步长与变步长求解器中均有连续与离散求解器。连续与离散求解器都是依靠模块来计算所有离散状态值。定义离散状态的模块负责在每个采样时间点计算离散状态值，连续求解器是通过数值积分来计算定义连续状态的模块的状态值。在选择求解器时，必须先确定模型中是否需要离散求解器。在模型中若没有连续状态模块，Simulink会自动选择离散求解器（即便设定使用连续求解器），若有连续状态模型必须采用连续求解器。

（3）显式与隐式求解器

隐式求解器的应用主要解决模型中的刚性问题，显式求解器应用解决非刚性问题。譬如，在控制系统中，控制部件反应灵敏是快变的，具有小的时间常数，而受控对象一般惯性大、慢变的，具有大的时间常数。通常将具有非常不同时间尺度的系统称之为刚性系统，通俗讲，就是系统中含有时间快变和慢变分量（同时含有小时间常数和大时间常数的系统）。刚性系统有非常大的恢复能力使得快变化分量的扰动很快就衰减，当数值积分这样一个系统时，一旦快变分量消失时期望选取合适的时间步长用于计算慢变分量。故刚性系统的实质是要计算的解是慢变化，但存在迅速衰减的扰动，这样的扰动出现使得慢变解的数值计算复杂化。因此，对系统中的震荡现象，隐式求解远比显式求解稳定，但计算的消耗比显式求解大，它需要在仿真的每个步长利用Newton-like方法计算所产生的雅可比（Jacob）矩阵和代数方程组。为了减少计算消耗，Simulink提供了计算雅可比方法的参数，提高仿真性能。

（4）单步与多步求解器

在Simulink求解库中提供了单步与多步求解器。单步求解就是在计算系统当前时刻y(tn)，需要利用前一时刻y(tn-1)以及在tn-1与tn之间多个时间点的微分量（这些时间点称为微步长）；多步求解器就是利用系统前多个时刻的值计算当前时刻的值。Simulink提供了一个显式多步求解器ode113和一个隐式多步求解器ode15s，这两个都是变步长求解器。

（5）变阶式求解器

Simulink提供两种变阶式求解器，ode15s求解器利用1阶到5阶仿真；ode113应用1阶到13阶。对于ode15s可以设置最高阶次。

 

2.3 Simulink仿真参数设置界面

Solver 面板：

(1)仿真时间设置：

Start time 开始时间：仿真和生成代码为双精度值，单位秒；参数名称为StartTime，参数类型为string。

Stop time 结束时间：仿真和生成代码为双精度值，单位秒；参数名称为StopTime，参数类型为string；此值应不小于Start time(若相等，则只运行一步)，可以设置为无穷大inf。

(2)求解器设置：不同的求解器，具体设置参数也不尽相同，这里指说明共同部分。

变步长求解器的配置参数包含以下各项：

Solver

Max step size：设置最大步长，缺省为auto，即为仿真时间历程的1/50；参数名称为MaxStep。

Min step size：设置最小步长，缺省为auto，即为不限制警告数量，最小步长近似机器精度；可以设置为一个大于零的实数，或者两个元素的数组(在产生错误警告前，第一个元素最小步长，第二个元素为最大步长)，参数名称为MinStep

Initial step size：求解器第一步执行的时间步长。

Relative tolerance

Absolute tolerance

Shape preservation

Initial step size

Number of consecutive min steps

Zero-crossing control

Time tolerance

Number of consecutive zero crossings

Algorithm

 

定步长求解器的设置包含以下参数：

Solver

Periodic sample time constraint

Fixed-step size (fundamental sample time)

Tasking mode for periodic sample times

Higher priority value indicates higher task priority

Automatically handle rate transitions for data transfers

 

2.4 选择求解器

求解器选择标准。仿真模型的合适求解器的选择取决于以下特性：

1. 系统动态特性
2. 解稳定性
3. 计算速度
4. 求解器稳健性

 

理想情况下，所选择的求解器应该：

1. 成功解算模型。
2. 对于变步长求解器，提供的解在指定的容差范围内。
3. 在合理的时间内解算模型。

 

图 1 Simulink求解器和选择流程

 

对于稍微复杂的问题，仅仅通过以上流程难以做出最有决定，通常需要尝试使用不同求解器进行仿真，以迭代方法为选择求解器。将多个求解器的仿真结果进行比较，然后从中选择一个性能最佳、开销最少的求解器。

 

通用的求解器选择流程：

1. 使用 auto 求解器。新模型默认情况下将其求解器选择设置为 auto 求解器。auto 求解器会为模型推荐定步长或变步长求解器以及最大步长。有关详细信息，请参阅 使用自动求解器选择求解器 。
2. 如果对使用 auto 求解器的仿真结果不满意，可在模型配置参数的求解器窗格中选择求解器。
3. 在编译和仿真模型时，可以基于模型的动态特性选择求解器。变步长求解器更适合纯连续模型，如质点弹性阻尼系统的动态特性。对于包含多个开关的模型（如逆变电力系统），建议使用定步长求解器，因为求解器重置次数会导致变步长求解器像定步长求解器那样工作。

 

注意：

当模型将需要用于生成代码进行部署时，只能使用定步长求解器。如果您在仿真过程中选择了变步长求解器，请使用它来计算部署时定步长求解器需要的步长。

 

3. 定步长求解器 fixed step discrete solver

 

顾名思义，定步长求解器在仿真求解过程使用固定的步长。通常来说，步长越小仿真精度就越高，但是其代价则是运算负荷更大仿真时间更长。

3.1 定步长离散求解器 fixed step discrete solver

 

定步长离散求解器通过在当前时间点的基础上加上仿真步长来计算下一时间点。因此，仿真的精度和时间长度取决于仿真步长的大小，步长越小精度越高。仿真步长可以任意设置，当步长设置为缺省的auto时，且模型中含有离散采样模块，Simulink会自动选择模型的基础采样时间（fundamental sample times）作为步长，若没有则默认整个仿真只有50步，仿真步长为仿真时间跨度的1/50，即：

 

对于离散系统来说，自然应该选择使用离散求解器。但是，即便示离散系统，也不一定非要使用定步长求解器。当离散系统中存在多个采样率时，定步长求解器和变步长求解器的行为是可能不一样的。

 

3.2 定步长连续求解器 fixed step continuous solver

 

当采用定步长连续求解器时，在当前时间点的基础上加上仿真步长来计算下一时间点，连续求解器使用数值积分技术计算模型的连续状态值，具体一点比如说，基于上一个时刻的状态值以及上一个时刻与当前时刻的中间若干时刻的状态的微分值来求解当前时刻的状态值。

对于一个没有状态变量或者只有离散状态的模型，Simulink将自动使用定步长离散求解器，即便你给它指定一个定步长连续求解器。

Simulink提供了两类定步长连续求解器：显式（explicit）定步长连续求解器和隐式（implicit）定步长连续求解器。两类求解器的差别在于仿真速度和稳定性。隐式求解器在每个仿真时间步需要进行更多的运算，但是也更加稳定。因此，在求解一个刚性系统时，隐式定步长连续求解器比显式定步长连续求解器更加合适。两类定步长连续求解器的选择基本流程如下图所示： 

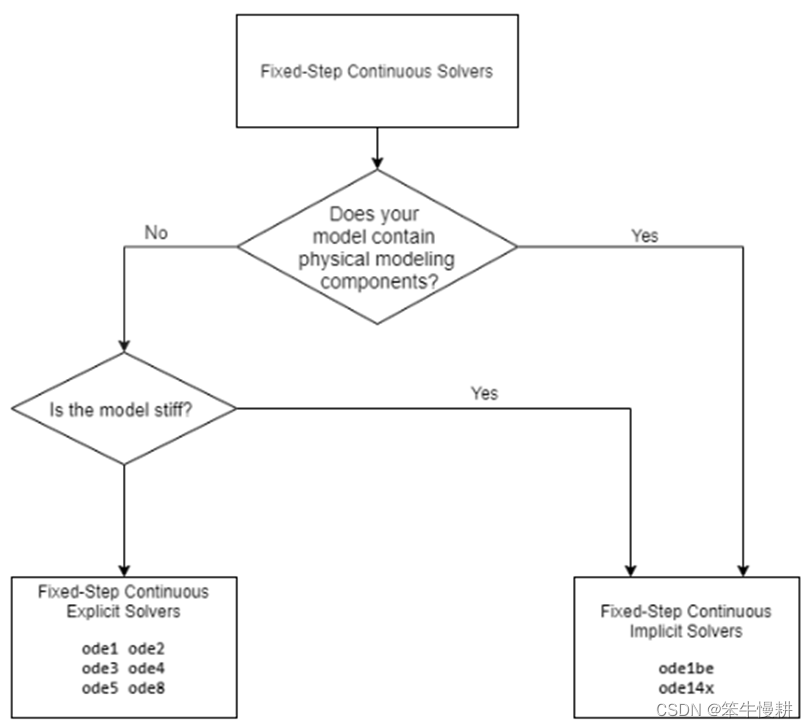
图 2 定步长连续求解器

 

3.2.1 显式定步长连续求解器

显式求解器基于关于上一时刻的状态以及状态的导数的显式的函数计算下一时刻的状态值，这个显式的函数关系表示如下:

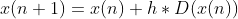
其中：

•         x 表示状态.
  •         Dx 表示求解器所采用的状态的导数的估计函数
    •         h 表示步长

 

Simulink提供了一系列的显式定步长连续求解器，它们的主要区别在于用于估计状态导数的数值积分技术（numerical integration techniques），如下所示：

这些求解器都没有误差控制机制（error control mechanism）. 所以，仿真误差（或反过来说accuracy）以及仿真时间直接取决于求解器所选择的步长。步长越小仿真误差越小，但是仿真时间越长。对于相同的步长，求解器阶数越高仿真结果越精确（误差越小）。

如果指定了定步长求解器类型，Simulink会缺省地选择FixedStepAuto solver. Auto solver会自动选择一个运算负荷适中且既能处理连续状态又能处理离散状态的合适的步长。与离散求解器相同，如果模型中存在离散采样率，Simulink会缺省地将步长设定为模型的基础采样时间间隔（fundamental sample time）。如果没有的话，Simulink也同样地自动将步长设定为(Tstop-Tstart)/50。 但是，这样可能会导致对连续状态的变化的计算不够精确。如果出现这种情况或者是担心出现这种情况，可以明确选择一个不同的求解器，或者明确指定一个固定的步长，或者两者合用以或者一个仿真误差和仿真时间之间的折衷。

 

​​​​​​​3.2.2 隐式定步长连续求解器

隐式求解器基于关于上一时刻的状态以及下一个时刻的状态的导数的隐式的函数计算下一时刻的状态值，这个函数的数学表达式如下:

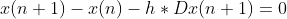
Simulink提供了两个定步长隐式求解器： ode14x and ode1be. 这些求解器结合使用牛顿方法（Newton's method）和外推（extrapolation）法 计算下一个时刻的状态值。用户可以指定牛顿方法的迭代次数和外推所使用的阶数。迭代次数越大、外推阶数越高能够获得更加精确的结果，当然其计算代价也相应增大。

 

4. Choose a Fixed-Step Solver

 

Simulink模型的求解器参数的缺省设定是auto, Simulink选择一个求解器的启发式探索方法（heuristics method）如下图所示：

​​​​​​​4.1 When to Use a Fixed-Step Solver

需要基于模型生成代码并作为产品部署到嵌入式平台运行的模型必须使用fixed-step solver。这是因为变步长求解器会根据系统状态，动态地调整仿真步长，这种可变的步长无法映射到目标系统的实时时钟上。

 

理论上来说，定步长连续求解器只要步长足够小，能够获得任意仿真精度。但是，这个当然伴随着代价，步长越小运算负荷越大，仿真时间也会越长。因此需要取得仿真精度与运算负荷之间的折衷。通常需要进行一些实验和分析以确定用于最终产品部署的固定步长.

 

​​​​​​​4.2 选择定步长的基本流程

 

Step1：使用变步长求解器获得一个基线(baseline)结果

Step1-1 确定一个可以接受的误差容限（ acceptable error tolerances）

Step1-2 选择一个可变步长求解器，使用auto或者指定一个明确的求解器。Additionally, enable the Save states, Save time, and Save outputs parameters in the Data Import/Export pane of the Model Configuration Parameters. Set the logging format for your model to Dataset to allow the Simulation Data Inspector to log the signals.

Step1-3 执行仿真。这个结果将作为基线结果用于后续对比

Step2：执行定步长仿真

关于定步长选择的考虑（Considerations for Selecting a Fixed Step Size）

最优步长必须在仿真速度、精度以及像代码生成、模型的物理或动力学特性等约束之间的折衷平衡。比如说，代码生成要求步长必须比处理器时钟周期要更大；仿真性能目标则要求步长必须小于任何一个模块的离散采样时间间隔；如果模型中包含周期性信号的话，步长必须要保证奈奎斯特采样率要求。

Step3：对比定步长仿真结果与基线结果

重复step2和step3以找到一个满足定步长仿真结果与基线结果对比在预定的相对误差容限以内的最大定步长作为选择结果。

关于如何进行有效的定步长仿真结果与基线结果的对比，更具体的信息可以进一步参考[2]。

 

5. 变步长求解器

 

变步长求解器在仿真过程中根据状态变化状况自适应地调整步长，比如说，在状态发生快速变化时会减小步长以减小误差，在状态发生变化缓慢时则会增加步长以降低运算负荷避免不必要的运算。虽然，计算步长本身会带来额外的运算开销，但是总体上仍然能够有效地降低仿真所需要的总的步数，并将状态发生快速变化或者分段连续的状态变化时的误差控制在指定要求的范围内。

将求解器配置（Solver configuration pane）的Type设定为Variable-step时，用户可以指定一种变步长求解器。与定步长求解器相同的是，变步长求解器也包含一个离散求解器和若干个连续求解器。与定步长求解器不同的是，仿真过程中步长随误差评估状况而动态变化。

选择连续求解器还是离散求解器取决于你的模型是否包含状态定义，以及如果有的话，所定义的状态的类型。如果模型中没有状态变量或者只有离散状态，则应该选用离散求解器；如果模型中有连续状态的话，则应该选择使用连续求解器。连续求解器使用数值积分（numerical integration）技术计算下一个时刻的连续状态值. 如果模型中没有状态变量或者只有离散状态，即便指定了连续求解器，Simulink也会自动选择使用离散求解器（所以，用户其实不用关心离散求解器和连续求解器的选择？）

 

​​​​​​​5.1 变步长离散求解器

 

对于不包含连续状态的模型，变步长离散求解器会自动地在减小步长以捕捉诸如过零（zero-crossing）之类的事件，或者增大步长以提高仿真速度。

考虑一个模型有两个离散输入信号源，一个采样周期为0.5s，另一个采样周期为0.75s，且均在时刻0进行第一次采样。采样变步长求解器和定步长求解器时的步长变化对比如下图所示。 

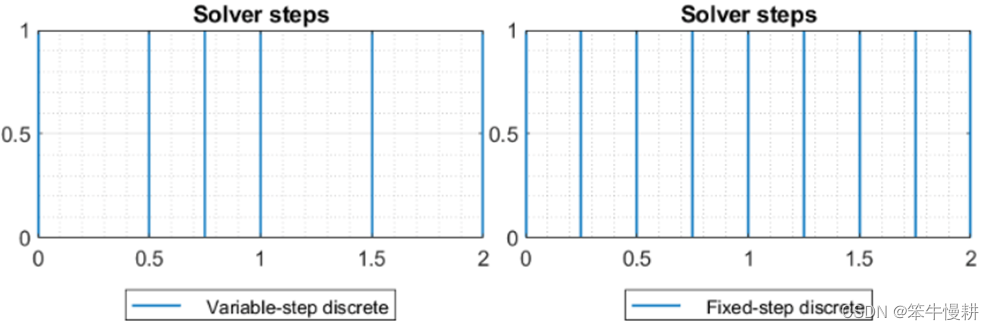
        定步长求解器必须以两个周期的最大公约数即0.25s作为其步长，只有这样它才能确保不会错过两个信号的任何一个有效采样时刻。而变步长求解器则只需要在两个周期的倍数集合的并集时刻进行计算，这样它所需要计算的次数会小于定步长求解器所需要计算的次数。 

​​​​​​​5.2 变步长连续求解器

变步长求解器在仿真过程中动态地调整步长，在满足所指定的误差容限的前提下尽量采用大的步长以降低运算负荷和仿真时间开销。

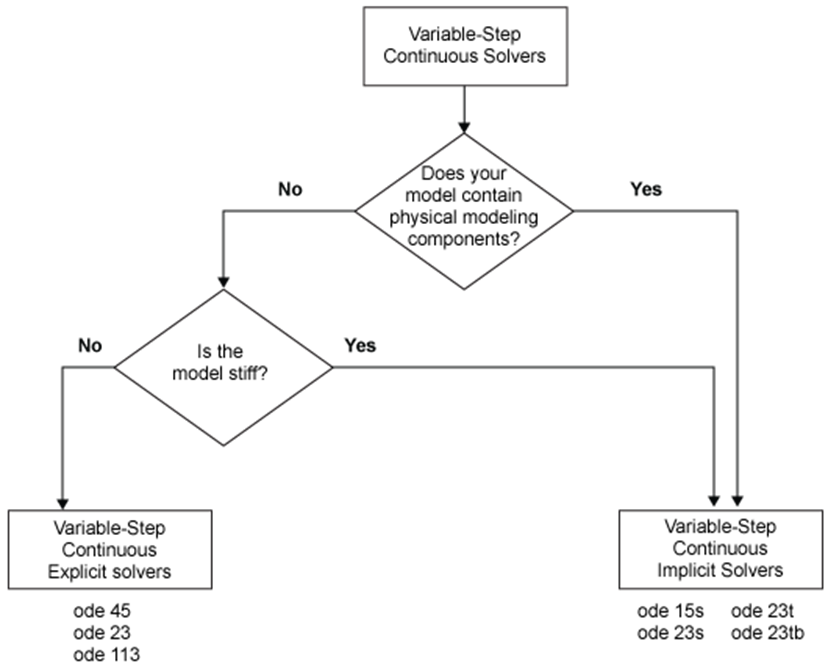
图 3 变步长连续求解器

 

变步长连续求解器的使用选择决策树如上图所示。还可以进一步将变步长求解器分为one-step or multistep, single-order or variable-order, and explicit or implicit. 更多信息参考 One-Step Versus Multistep Continuous Solvers.

​​​​​​​5.2.1 显式变步长连续求解器

Simulink提供了以下4种显式的变步长连续求解器： ode45; ode23; ode113; odeN. 它们的异同点对比如下表所示：

1. ode45基于显式Runge—Kutta(4，5)公式，Dormand—Prince对．它是—个单步求解器(solver)。也就是说它在计算y(tn)时，仅仅利用前一步的计算结果y(tn-1)．对于大多数问题．在第一次仿真时、可用ode45试一下．
2. ode23是基于显式Runge—Kutta(2，3)．Bogackt和Shampine对．对于宽误差容限和存在轻微刚性的系统、它比ode45更有效一些．ode23也是单步求解器．
3. odell3是变阶Adams-Bashforth—Moulton PECE求解器．在误差容限比较严时，它比ode45更有效．odell3是一个多步求解器，即为了计算当前的结果y(tn），不仅要知道前一步结果y(tn-1)，还要知道前几步的结果y(tn-2)，y(tn-3)，…；

【建议】

当仿真速度需要优先考虑时可以选用odeN，比如说：

1. 模型的动态行为中包含大量的过零和/或求解器复位
2. SolverProfiler对模型的分析中没有发现任何失败的仿真步尝试​​​​​​​

5.2.2 隐式变步长连续求解器

当仿真问题为刚性问题时，可以尝试使用以下隐式的变步长连续求解器：ode15s; ode23s; ode23t; ode23tb. 它们的异同点对比如下表所示：

1. odel5s是基于数值微分公式(NDFs)的变阶求解器．它与后向微分公式BDFs(也叫Gear方法)有联系．但比它更有效．ode15s是一个多步求解器，如果认为一个问题是刚性的，或者在用ode45s时仿真失败或不够有效时，可以试试odel5s。 odel5s是基于一到五阶的NDF公式的求解器．尽管公式的阶数越高结果越精确，但稳定性会差一些．如果模型是刚性的，并且要求有比较好的稳定性，应将最大的阶数减小到2．选择odel5s求解器时，对话框中会显示这一参数． 可以用ode23求解器代替。odel5s，ode23是定步长、低阶求解器．
2. ode23s是基于一个2阶改进的Rosenbrock公式．因为它是一个单步求解器，所以对于宽误差容限，它比odel5s更有效．对于一些用odel5s不是很有效的刚性问题，可以用它解决．
3. ode23t是使用“自由”内插式梯形规则来实现的．如果问题是适度刚性，而且需要没有数字阻尼的结果，可采用该求解器．
4. ode23tb是使用TR-BDF2来实现的，即基于隐式Runge—Kutta公式，其第一级是梯形规则步长和第二级是二阶反向微分公式．两级计算使用相同的迭代矩阵．与ode23s相似，对于宽误差容限，它比odel5s更有效．

5.3 ​​​​​​​变步长求解器的误差容限（Error Tolerances）

5.3.1 局部误差 Local Error

变步长求解器使用标准的误差控制技术监控每个仿真时间步局部误差。在每个仿真时间步（time step）求解器计算该时间步终点时刻的各状态值并估计各局部误差（local error）。比较这个局部误差与可接受的误差容限（包括相对误差容限rtol和绝对误差容限atol。如果任何一个状态的局部误差超过了可接收误差，求解器将减小步长再次尝试。

相对误差容限Relative tolerance 表示局部误差与状态值本身的比率（绝对值）的门限。缺省的门限为1e-3, 意味着要求局部误差不超过状态值本身的0.1%.

绝对误差容限Absolute tolerance ，顾名思义就是指针对误差（绝对值）本身的门限，事实上是表示当前状态值趋近于0时所允许的最大误差值。

求解器要求状态i的误差满足以下条件：

        ​​​​​​​        

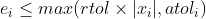
下图所示为在不同区间分别由相对误差容限和绝对误差容限所决定的可接受误差的示例：

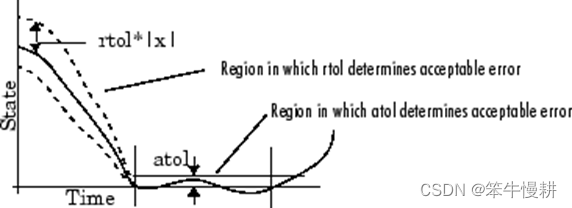
图 4 相对误差容限和绝对误差容限

 

​​​​​​​5.3.2 绝对误差容限Absolute Tolerances

在模型的配置参数对话框（Solver pane of the Configuration Parameters dialog box）中可以设置全局的绝对误差容限。这个误差容限适用于所有状态，可以设置为auto或者一个标量值.如果设置为auto（缺省值）的话，Simulink首先会根据相对误差容限为每个状态设定一个绝对误差容限，如果相对误差容限reltol大于等于1e-3, abstol会被初始化为1e-6； 如果reltol < 1e-3, abstol则会初始化为reltol * 1e-3. 随着仿真时间的推移，每个状态的绝对误差容限会更新为该状态到当前为止的最大值乘以该状态的相对误差容限。因此，如果一个状态值从0变到1，而reltol=1e-3,abstol则开始时被初始化为1e-6，然后到仿真结束时更新为1e-3。如果一个状态值从0变到1000的话，abstol到仿真结束时将更新为1。

如果根据以上规则确定的绝对误差容限不合适的话，用户可以自己确定一个合适的值。比如说，通过仿真试错的方式来确定合适的值。用户也可以设定AutoScaleAbsTol来使能绝对误差容限的自适应调节过程，详细参见Auto scale absolute tolerance.

有若干个模块允许用户指定绝对误差容限用于求解状态值，如下所示：

• Integrator
• Second-Order Integrator
• Variable Transport Delay
• Transfer Fcn
• State-Space
• Zero-Pole

为这些模块所指定的绝对误差容限覆盖了上述的在Configuration Parameters dialog box中所作的全局设定。在有些场合下，用户可能会希望覆盖全局设定，比如说，由于所有的模块状态的变化幅度的差异非常大，导致全局设定没能提供充分的误差控制

模块的绝对误差容限有以下设定选项:

• auto
• -1(same as auto)
• positive scalar
• real vector (having a dimension equal to the number of corresponding continuous states in the block)​​​​​​​

5.3.3 小贴士

如果你选择设置绝对误差容限的话，请注意，设定的太小会导致求解器在状态值接近零的区间会需要超额的仿真步数，从而导致仿真变慢。另一方面，如果设定得太大的话，当一个或者多个状态趋近于零，仿真结果可能会变得不够准确。理由参见以上图3。

一旦仿真结束后，你可以验证你的仿真结果的准确度。具体做法是，将绝对误差容限设定为一个更小的值重新仿真，如果两次仿真的结果之间的差异足够小的话，就说明仿真结果足够准确，也就意味着绝对误差容限是合理的。

 

6. 一个简单例子：求解器选择对仿真结果的影响

考虑如下图所示的一个简易simulink模型，由于各模块的作用都是显而易见的，这里不做过多解释。

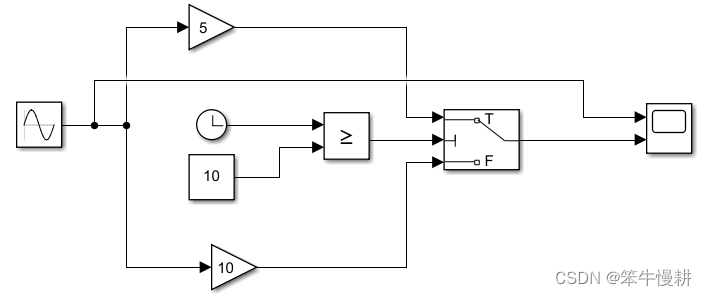
这个模型中没有离散采样模块，求解器的缺省配置如下图所示：

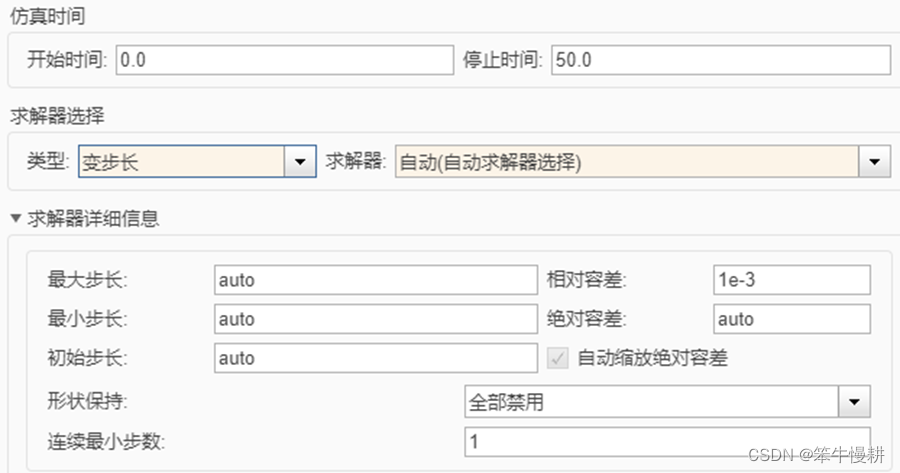
仿真结果如下图所示，很显然，仿真输出结果曲线不够光滑，连续性不够好。这就是因为缺省配置的条件下，采用步数为50，即步长为1. 对于本例这样的简易模型，即便如此粗糙的配置，仿真误差也在误差容限范围以内（事实上由于并没有做什么处理，在所仿真的采样时刻，误差总是0）. 

如果想要仿真输出波形显得更光滑一些的话，可以采用定步长求解器，并将步长设置更小一些，如下所示： 

这样我们就得到了如下图所示的光滑输出波形了。

 

本文内容主要编译自[1]~[4]。最后一个示例取自[5]。

[1] Fixed Step Solvers in Simulink - MATLAB & Simulink - MathWorks 中国

[2] Choose a Fixed-Step Solver - MATLAB & Simulink - MathWorks 中国

[3] Variable Step Solvers in Simulink - MATLAB & Simulink - MathWorks 中国

[4] 选择求解器 - MATLAB & Simulink - MathWorks 中国

[5] 姚俊，马松辉编著，Simulink建模与仿真