微机原理笔记 - 主页

第 1 章 微型计算机基础概论

1. 微型计算机系统

（1）微型控制机是嵌入计算机的一种 8 位或 16 位机，没有操作系统。

（2）计算机的基本组成（ 3+1 结构）：CPU 、储存器、I/O 和应用软件。

（3）冯·诺依曼计算机：以计算器为核心，以存储程序原理为基础。

• 存储程序原理：CPU 控制程序逐条自动运行。
  

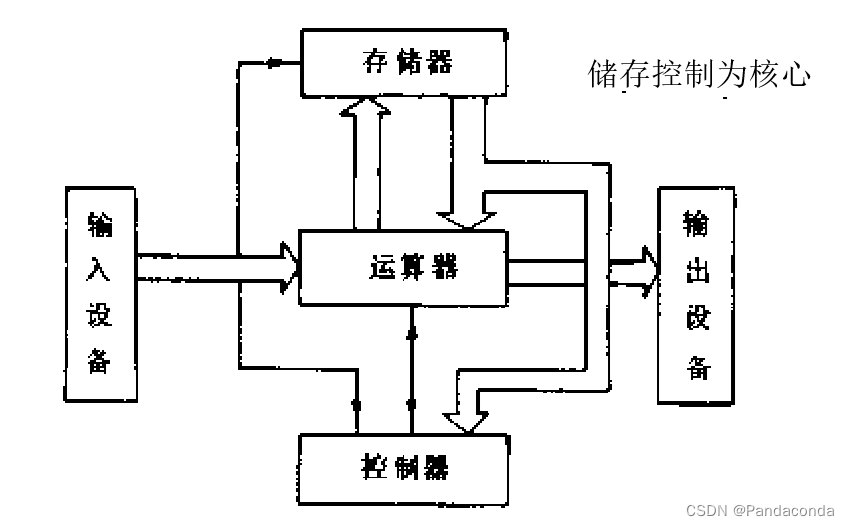
（4）微机系统组成

2. 计算机中的数值及编码

（1）常用记数制

• 二进制： 数字后面加 B ，如 1001B 等。

  eg. 1101.101=1×2³+1×2²+0×2¹+1×2⁰+1×2^-1+1×2^-3

• 十进制： 一般不加，如 1001 等。

  eg. 1234.5=1×10³ +2×10² +3×10¹ +4×10⁰ +5×10^-1

• 十六进制：数字后面加 H ，如 1001H（如果开头是字母，则需要加0，如0A5H）等。

  eg. DFC.8=13×16²+15×16¹+12×16⁰+8×16^-1

• 八进制： 数字后面加 O ，如 1001O 等。

（2）各数制之间的转换

• 十进制与二进制

eg.

• 二进制与十六进制

eg.

（3）二进制编码

• BCD 码：只是为了方便认识十进制，用 0000 - 1001 表示 0 - 9 。

  eg. [0100 1001 0001.0101 1000]_BCD = 491.58

  eg. 0101 1000B = 88D = [1000 1000]_BCD

• ASCII码（字母大小写的转化只需加减一个 20H 即可）

0 - 9 ： 30H - 39H

A - Z ： 41H - 5AH

a - z ： 61H - 7AH

奇偶校验位： 由于 H 表示高 3 位，故剩下那一位就是奇偶校验位。比如 0100 0001 和 1100 0001 都表示 A，前面那个偶码，后面那个是奇码。

3. 无符号二进制数的运算

（1）逻辑运算

• 与运算（&）

• 或运算（|）

• 非运算（~）

• 异或运算（^）

（2）乘除法

• 一个数乘以 2 相当于该数左移一位，除以 2 则相当于该数右移 1 位。

  eg. 00001011 × 0100(4) = 00101100B（相当于左移两位）

  eg. 00001011 ÷ 0100(4) = 00000010B（相当于右移两位）

（3）无符号数的表示范围

• 一个n位的无符号二进制整数X，其表示范围为 0 ≤ X ≤ 2n-1（n = 8, 255）。

• 如果发生溢出，则 C_n-1 = 1 。

  8 位可以编 256 个，0 - 255，C₇ = 1

  16 位可以编 65536 个，0 - 6553515，C₁₅ = 1

（4）74L138 译码器

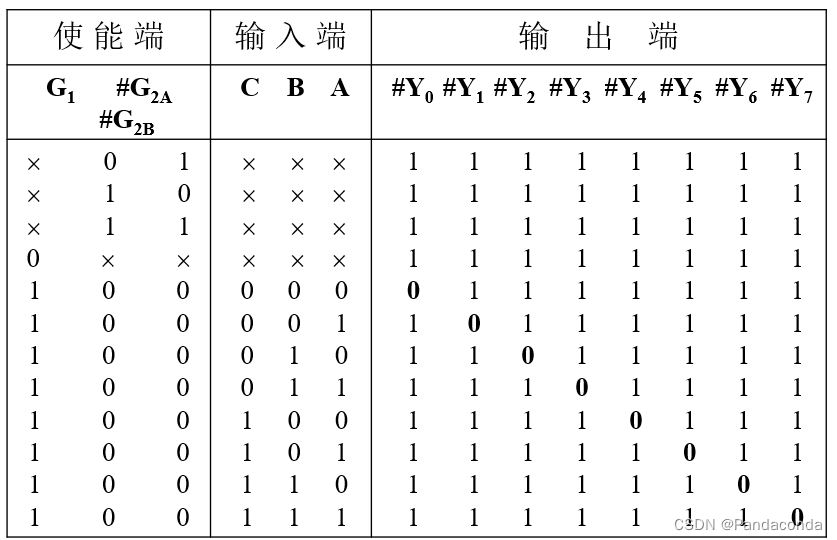
4. 带符号二进制数的运算

（1）有符号二进制数的表示

• 原码

  一个8位的二进制表示一个带符号数，最高有效位D7位为符号位。

  eg. +1 表示为：0000 0001 B

  eg. +127 表示为：0111 1111 B

  eg. -1 表示为：1000 0001 B

  eg. -127 表示为：1111 1111 B

  带符号二进制数不能用原码而是补码来表示，因为原码的 + 0 和 - 0 不一样，会少表示一个码。

• 反码

  • 若 X > 0 ，则 [X]_反 = [X]_原
  • 若 X < 0 ，则 [X]_反 = 对应原码的符号位不变，数值部分按位求反

  eg. X = - 52 = - 0110100，则 [X]_原 = 1011 0100，[X]_反 = 1100 1011

• 补码

  • 若 X > 0 ，则 [X]_补 = [X]_反 = [X]_原
  • 若 X < 0 ，则 [X]_补 = [X]_反 + 1

  eg.

[+0]_补 = [+0]_原= 0000 0000

[-0]_补 = [-0]_反 + 1 = 1111 1111 + 1 = 0000 0000（对8位字长，进位被舍掉）

∴ [+0]_补 = [-0]_补 = 0000 0000，并且将 1000 0000 定义为 -128

原码： -127 ~ +127 补码： -128 ~ +127

（2）带符号数的运算

• 通过引进补码，运算方法和二进制运算相同（可以将减法变成加法）。

  eg.

（3）补码与十进制数的转换

• 正数

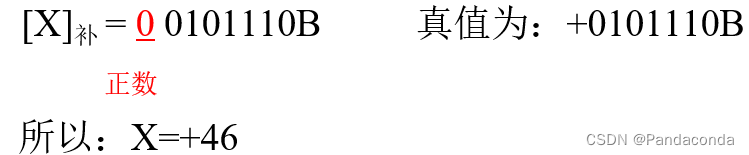
• 负数（补码求补 = 原码）

真值转补码：

X = -46 = - 0010 1110

[X]_补 = 1101 0010

（4）有符号数的溢出问题

• 判断方法： 两个8位带符号二进制数相加或相减时，若 C7 异或 C6＝1，则结果产生溢出。

  • 两负数相加可能溢出

• 两正数相加可能溢出

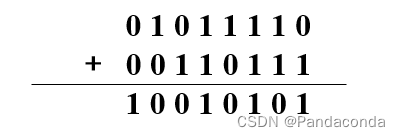
• 两负数相加可能没有溢出

无符号数的溢出系统不会报错，需要程序员自行处理。

有符号数的溢出系统会报错。

重点

• 开头是字母的十六进制书写

• 熟练字节十进制与二进制的相互转换

• BCD 码的定义

• ASC 码的注意事项

• 二进制的乘除运算

• 8、16 位数的表示范围

• 带符号负数用补码

• -128 的补码定义

• 负数的补码求补才能求真值，方法。

• 二进制数运算的溢出问题