我们知道，当快速排序的递归层次越多，那么栈就有可能会溢出。那么我们就需要写一个非递归的。

1. 快速排序(非递归)

那么我们怎么把递归改成非递归的呢？
我们需要利用栈这个数据结构。
我们看下面的一组数据：

首先，我们将第一个元素的下标和最后一个元素的下标放到栈中：

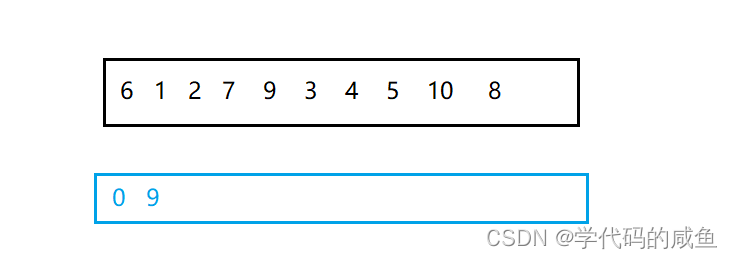
然后，我们将9取出来放到right，将0取出来放到left里，然后做单趟排序。
排完序是这个样子：

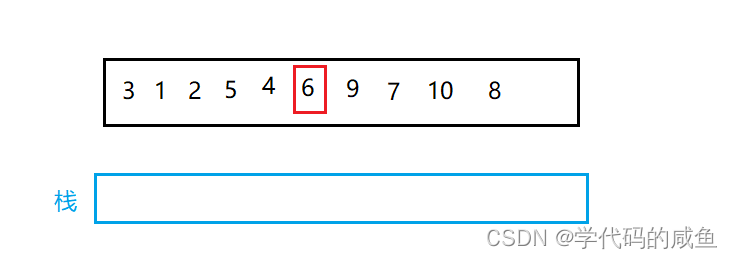
然后，我们在将6的左区间和右区间有序该怎么办呢？我们将0和key-1入栈，然后将key+1和n-1入栈。

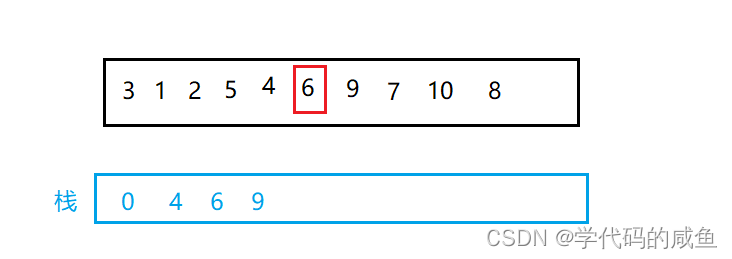
我们再出栈将9放到right，将6出栈放到left，再做单趟排序。
也就是6的右区间做单趟排序：

然后，我们再将9的左区间入栈，9的右区间入栈。
因为，9的右区间只有一个数不需要入栈，只入左区间。

然后，我们将7出栈放到right里，将6出栈放到left里。再做单趟排序：

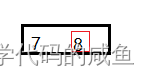
此时，我们将8的左右区间入栈，8的左区间只有一个不入栈，8的右区间没有也不入栈。此时，栈里面还有0和4，也就是6的左区间，思路是一样的。
完整代码：

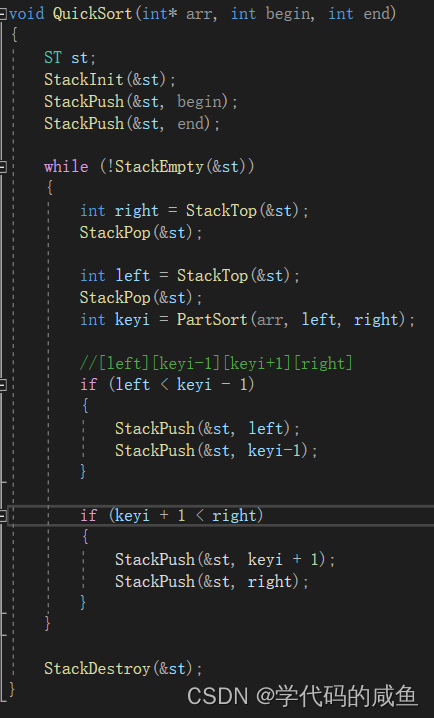
同样道理，我们也可以用队列来实现。

2. 归并排序

2.1 基本思想

归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。 归并排序核心步骤：

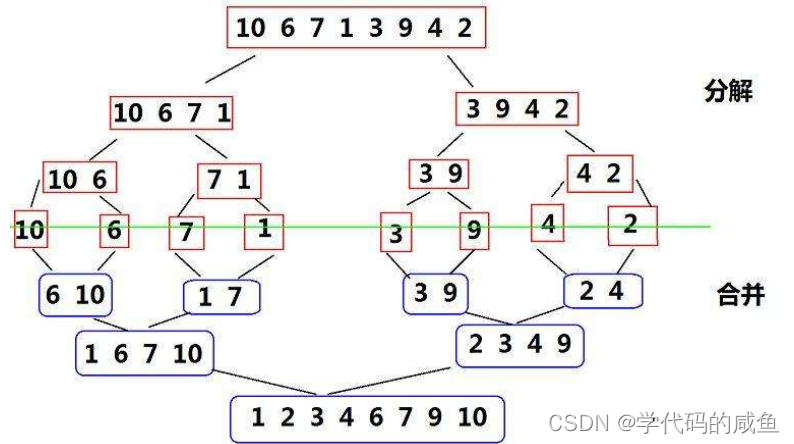
动图演示：

2.2 递归版本具体实现

其实我们就是将序列给分解成不能在分解的子问题。也就是只有1个或者没有的时候，我们就可以开始合并了。
在合并的时候我们要额外开辟一个数组，因为如果在原数组合并，会把值给覆盖。
首先，我们来看一下分解的代码：

当begin和end都为0时，就返回，然后递归右区间，begin和end都为1时，返回。此时，我们就可以合并[0,0]和[1,1]两个区间的值了。其它的道理类似。

那么，在说一下如何合并：

我们以这组序列为例：
首先，我们需要将[0,0]和[1,1]合并，就是比较大小，小的先放到tmp数组里，然后再继续比较。当合并完之后，我们将tmp里数据复制到原数组中。

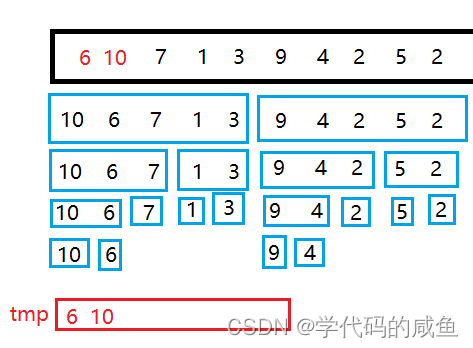
这样[0,1]区间就有序了，我们就开始合并[0,1]和[2,2]

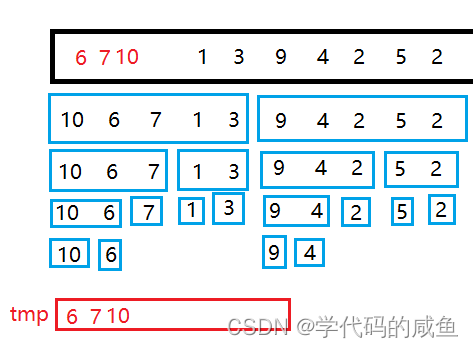
这样[0,2]就有序了，我们需要合并[3,3]和[4,4]

这样[0,2]和[3,4]都有序了，我们需要合并[0,2]和[3,4]

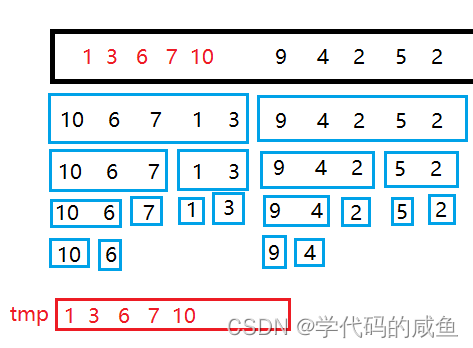
这样左区间就有序了，右区间也是同样的道理。
完整代码如下：

2.3 非递归版本具体实现

首先，我们看一下这组数据：

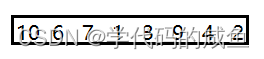
我们要归的话，需要一个一个归，10和6归，7和1归，3和9归，4和2归。
那么我们就可以定义一个gap代表要归并的个数。
当gap为1时，也就是一个一个来合并。

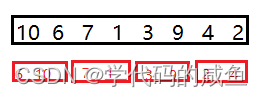
然后，我们将gap为2，这样就是两两合并。
也就是[0,1]和[2,3]合并，[4,5]和[6,7]合并。

然后就是四四合并，[0,3]和[4,7]合并。

从这里，我们可以看出gap从1变成2然后变成4是2倍增长。
那么我们就可以先控制gap了：

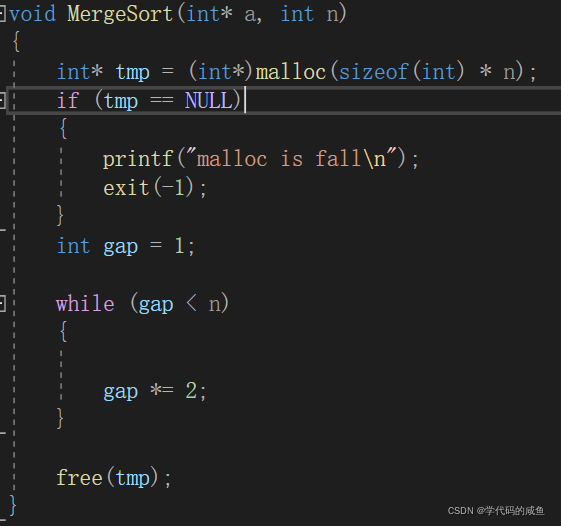
然后，我们需要控制数组下标了，我们可以定义一个i来控制，首先第一步是下标0和下标1合并，第二步是下标2和下标3合并…也就是i=0，i=2，i=4…
当两两合并时，[0,1]和[2,3]，[4,5]和[6,7]，也就是i=0，i=4，i=8…
那么我们就可以控制下标了：

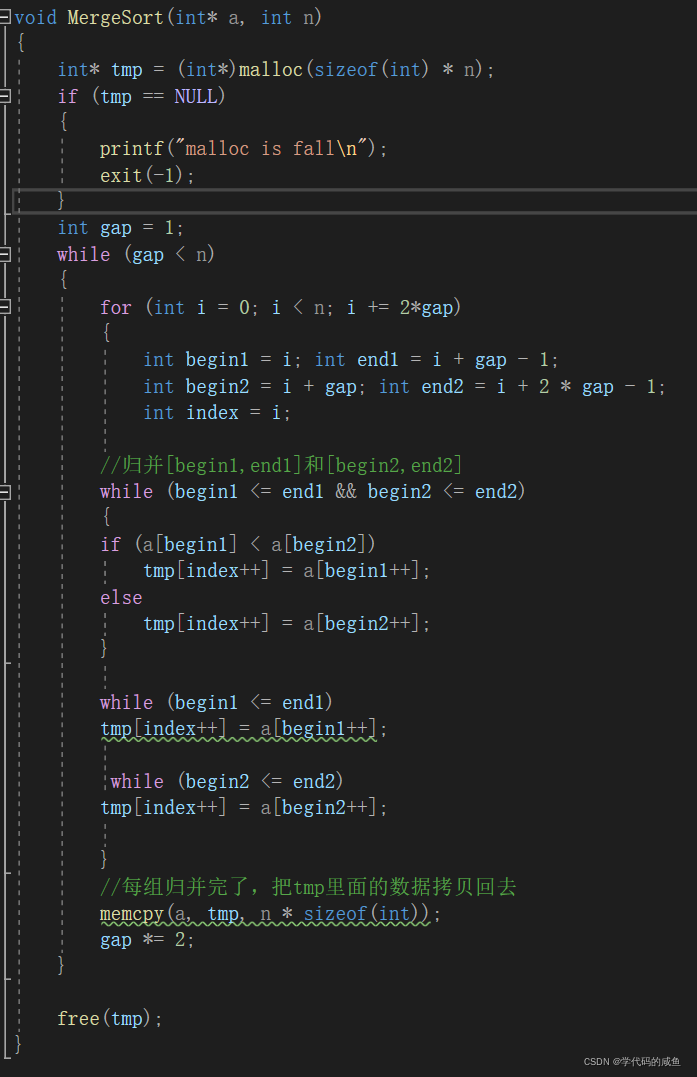
那么这样写有没有什么问题呢？我们来看下面的数据：

如果gap为2时，也就是两两合并。[0,1]和[2,3]合并，[4,5]和[6,7]合并，[8,9]和[10,11]合并，但是[10,11]begin2和end2已经越界了。

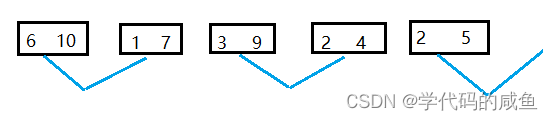
当gap为4时，就是[0,3]和[4,7]合并，然后[8,11]和[12,15]合并。这时end1，begin，end2都越界了。

那么我们就要想一下该如何去解决这个越界问题。
从上面的分析我们可以得出，end1，begin2，end2都可能会越界。所以这三个越界我们都需要控制。
在这里分为三种情况：
第一种情况：end1没越界，begin2没越界，end2越界。那么如果end2>=n时，我们就将end2赋值成n-1

第二种情况：end1没越界，begin2越界，end2越界。那么第二个区间就不存在，我们就要将第二个区间弄成一个不存在的区间

第三种情况：end1越界，那么begin2，end2肯定也越界了。那么我们需要将end1赋值成n-1，begin2和end2按照上面的再修改。

这样就可以控制非递归的边界问题了。完整代码如下：

2.4 复杂度分析

2.4.1 时间复杂度

我们先说一下时间复杂度。

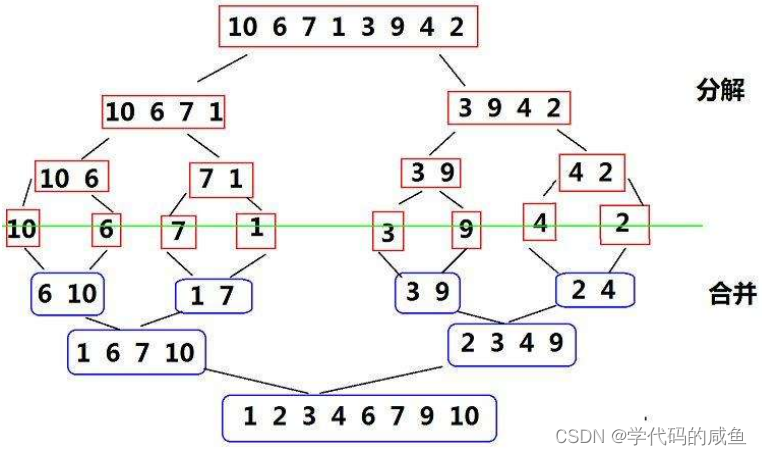
归并排序分为分解和合并。首先分解我们可以看到它每次都是二次等分。一共n个数，每次都是二分，也就是2^x=n，x=logn。所以，分解有logn层。

合并其实和分解差不多，但合并需要排序，也就是每次合并都要过一遍n，然后有logn层，也就是n*logn。

所以时间复杂度就为logn+nlogn，在大O的渐进表示法为O(nlogn)。

2.4.2 空间复杂度

空间复杂度就很简单，我们可以看出它需要额外开辟n个数据的空间。然后我们要看它的递归深度，我们可以看出它递归有logn层，每次递归里的空间是常数量，也就是O(1)，所以，空间复杂度就为n+logn，又因为n远大于logn，所以空间复杂度为O(N)。

2.5 归并排序的外排序

在我们说的这些常见的算法排序中，都能实现内排序。什么是内排序呢？
内排序：就是数据存在内存中。下标随机访问，速度快。
但是，只有归并排序才能做外排序。
那什么是外排序呢？
外排序：数据元素太多不能同时放在内存中，而放在磁盘中，串行访问，速度慢。

现在有这样一个问题：
10亿个整数文件，只给1G的运行内存，请对文件中的10亿个数进行排序。
这个问题我们该如何解决呢？
首先，我们要知道10亿个整数我们需要多少内存呢？
1G=1024MB，1024MB=10241024KB，1024KB=10241024*1024byte
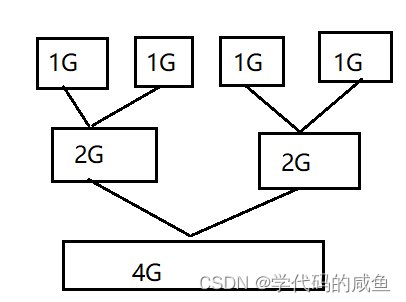
所以1G大约等于10亿字节。那么10亿个整数就是40亿字节，差不多是4G。
解决方法：将文件分成4等分，每份为1G，分别读到内存里排序，排完序，再写回磁盘小文件。然后再在磁盘里归并。